The wavelength of light in vacuum is when it travels normally through diamond of thickness 1.0 mm find the number of waves of light in 1.0 mm of diamond. (Refractive index of diamond =2.417)
4834 waves
5834 waves
4384 waves
6834 waves
The correct Answer is:A
To solve the problem, we need to determine the number of waves of light that fit into a diamond of thickness 1.0 mm, given the wavelength of light in vacuum and the refractive index of diamond.
1. Identify Given Values:
- Wavelength of light in vacuum, \lambda = 5000 \, \text{Å} = 5000 \times 10^{-10} \, \text{m}
- Thickness of diamond, d=1.0mm=1.0×10−3m
- Refractive index of diamond, μ=2.417
2. Calculate the Wavelength of Light in Diamond:
- The wavelength of light in a medium is given by the formula:
λ′=λμ
- Substituting the values:
λ′=5000×10−10m2.417
- Calculate λ′:
λ′≈2070.4×10−10m=2.0704×10−7m
3. Calculate the Number of Waves in the Diamond:
- The number of waves N in the medium can be calculated using the formula:
N=dλ′
- Substituting the values:
N=1.0×10−3m2.0704×10−7m
- Calculate N:
N≈4834.1
4. Final Result:
- Since the number of waves must be a whole number, we round it down to:
N≈4834
Thus, the number of waves of light in 1.0 mm of diamond is approximately 4834.
- Wavelength of light in vacuum, \lambda = 5000 \, \text{Å} = 5000 \times 10^{-10} \, \text{m}
- Thickness of diamond, d=1.0mm=1.0×10−3m
- Refractive index of diamond, μ=2.417
- The wavelength of light in a medium is given by the formula:
λ′=λμ
- Substituting the values:
λ′=5000×10−10m2.417
- Calculate λ′:
λ′≈2070.4×10−10m=2.0704×10−7m
- The number of waves N in the medium can be calculated using the formula:
N=dλ′
- Substituting the values:
N=1.0×10−3m2.0704×10−7m
- Calculate N:
N≈4834.1
- Since the number of waves must be a whole number, we round it down to:
N≈4834
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE -I (LEVEL-II LECTURE SHEET (ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTIONS)
29 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE -I (LEVEL-II LECTURE SHEET (ADVANCED) MORE THAN ONE CORRECT TYPE QUESTIONS)
3 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - PRACTICE SHEET (EXERCISE III LEVEL -II (ADVANCED) INTEGER TYPE QUESTIONS)
4 Videos
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
10 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - PRACTICE EXERCISE
106 Videos
Similar Questions
If the speed of light in diamond is 1.24×108 m/s, find its refractive index.
View SolutionWhen light of wavelength 5000 Å in vacuum travels through same thickness in glass and water, the difference in the number of waves is 400. Find thickness. (Refractive indices of glass and water are 32 and 43 respectively)
View SolutionThe speed of light in air is 3×108 m/s. Find its speed in diamond if the refractive index of diamond is 2.42 .
View SolutionRefractive index of diamond with respect to glass is 1.6 and absolute refractive index of glass is 1.5. Find out the absolute refractive index of diamond.
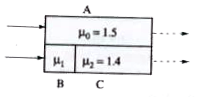
View SolutionA slab of transparent materials is made as shown in the figure. Monochromatic parallel beams of light are normally incident on the slabs. The thickness of C is twice the thickness of B. The number of waves is A= the number of waves in the combination of B and C. The refractive index of material A is μ0=1.5 and that of C is μ2=1.4
View SolutionLight of wavelength 4500Å in vacuum enters into a glass block of refractive index 1.5. What is the wavelength of light in the glass block?
View SolutionWhen white light is incident normally an oil film of thickness 10−4cm and refractive index. 1.4 then the wavelength which will not be seen in the reflected system of light is
View SolutionA glass sheet 12×10−3 mm thick (μg=1.5) is placed in the path of one of the interfering beams in a Yongs's double slit interference arrangement using monochromatic light of wavelenght 6000 A. If the central bright fringe shifts a distance equal to width of 10 bands. What is the thickness of the sheet of diamond of refractive index 2.5 that has to be introduced in the path of second beam to bring th ecentral bright fringe to original position?
View SolutionSpeed of light in vacuum is 3×108m/s. Range of wavelength of visible light is 4000Å−7000Å. Find the range of frequency of visible light.
View SolutionA ray of light passes through two slabs of same thickness. In the first slab n1 waves are formed and in the second slab n2. Find refractive <br> index of second medium with respect to first.
View Solution
