The focal lengths of a lens are in the ratio 8:3 when it is immersed in two different liquids of refractive induces 1.6 and 1.2 respectively. The refractive index of the material of the lens is
1.25
1.5
1.8
2
The correct Answer is:D
To solve the problem, we will use the lens maker's formula and the information given about the focal lengths in two different liquids.
1. Understanding the Problem:
We have a lens with focal lengths in the ratio of 8:3 when immersed in two different liquids with refractive indices n1=1.6 and n2=1.2. We need to find the refractive index μl of the lens material.
2. Using the Lens Maker's Formula:
The lens maker's formula is given by:
1f=(μl−n)1R
where f is the focal length, μl is the refractive index of the lens, n is the refractive index of the medium, and R is the radius of curvature.
3. Setting Up the Equations:
For the first liquid (refractive index n1=1.6):
1f1=(μl−1.6)2R
For the second liquid (refractive index n2=1.2):
1f2=(μl−1.2)2R
4. Expressing Focal Lengths:
Rearranging the equations gives us:
f1=2Rμl−1.6
f2=2Rμl−1.2
5. Using the Ratio of Focal Lengths:
We know that:
f1f2=83
Substituting the expressions for f1 and f2:
2Rμl−1.62Rμl−1.2=83
The 2R cancels out:
μl−1.2μl−1.6=83
6. Cross-Multiplying:
Cross-multiplying gives:
3(μl−1.2)=8(μl−1.6)
Expanding both sides:
3μl−3.6=8μl−12.8
7. Rearranging the Equation:
Rearranging the equation to isolate μl:
12.8−3.6=8μl−3μl
9.2=5μl
Dividing both sides by 5:
μl=9.25=1.84
8. Final Answer:
The refractive index of the material of the lens is μl=1.84.
We have a lens with focal lengths in the ratio of 8:3 when immersed in two different liquids with refractive indices n1=1.6 and n2=1.2. We need to find the refractive index μl of the lens material.
The lens maker's formula is given by:
1f=(μl−n)1R
where f is the focal length, μl is the refractive index of the lens, n is the refractive index of the medium, and R is the radius of curvature.
For the first liquid (refractive index n1=1.6):
1f1=(μl−1.6)2R
For the second liquid (refractive index n2=1.2):
1f2=(μl−1.2)2R
Rearranging the equations gives us:
f1=2Rμl−1.6
f2=2Rμl−1.2
We know that:
f1f2=83
Substituting the expressions for f1 and f2:
2Rμl−1.62Rμl−1.2=83
The 2R cancels out:
μl−1.2μl−1.6=83
Cross-multiplying gives:
3(μl−1.2)=8(μl−1.6)
Expanding both sides:
3μl−3.6=8μl−12.8
Rearranging the equation to isolate μl:
12.8−3.6=8μl−3μl
9.2=5μl
Dividing both sides by 5:
μl=9.25=1.84
The refractive index of the material of the lens is μl=1.84.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE -I (LEVEL-II LECTURE SHEET (ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTIONS)
29 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE -I (LEVEL-II LECTURE SHEET (ADVANCED) MORE THAN ONE CORRECT TYPE QUESTIONS)
3 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - PRACTICE SHEET (EXERCISE III LEVEL -II (ADVANCED) INTEGER TYPE QUESTIONS)
4 Videos
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
10 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - PRACTICE EXERCISE
106 Videos
Similar Questions
Consider an equiconvex lens of radius of curvature R and focal length f. If f>R , the refractive index μ of the material of the lens
View SolutionFocal length of a convex lens of refractive index 1.5 is 2 cm. Focal length of lens when immersed in a liquid of refractive index 1.25 will be
View Solution
Knowledge Check
The radius of curvature of the curved surface of a plano-convex lens is 20cm. If the refractive index of the material of the lens be 1.5, it will
Aact as a convex lens only for the objects that lie on its curved side.Bact as a concave lens for the objects that lie on its curved side.Cact as a convex lens irrespective of the side on which the object lies.Dact as a concave lens irrespective of side on which the object lies.
The focal length of lens of refractive index 1.5 in air is 30cm When it is immersed in water of refractive index 43 ,then its focal length will be
View SolutionA thin convex lens made from crown glass (μ=3/2) has focal length f. When it is measured in two different liquids having refractive indiced 4/3 and 5/3, it has the focal length f1 and f2 respectively. The correct ralation between the focal lengths is
View SolutionA plano-convex lens is made of refractive index of 1.6. The focal length of the lens is
View SolutionFor a plano convex lens, the radius of curvature of convex surface is 10 cm and the focal length is 30 cm. The refractive index of the material of the lens is
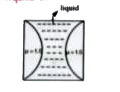
View SolutionThe effective focal length of the lens combination shown in figure is -60 cm. The radius of curvature of the curved surfaces of the plano-convex lenses are 12 cm each and refractive index of the material of the lens is 1.5. The refractive index of the liquid is
View SolutionA double convex lens of focal length 30 cm is made of glass. When it is immersed in a liquid of refractive index 1.4, the focal length is found to be 126 cm. The critical angle between glass and the liquid is
View SolutionFind the radius of curvature of the convex surface of a plan-convex lens, whose focal length is 0.3 m and the refractive index of the material of the lens is 1.5.
View Solution
