The work done by a force during a displacement is given by . Suppose a force of 12 N acts on a particle in vertically upward directionand the particle is displaced through 2.0 m in vertically downward direction. Find the work done by the force during this displacement.
The correct Answer is:B, D
To find the work done by the force during the displacement, we can follow these steps:
Step 1: Identify the Force and Displacement Vectors
- The force →F is acting in the vertically upward direction with a magnitude of 12 N. We can represent this as:
→F=12^k
- The displacement →r is in the vertically downward direction with a magnitude of 2 m. We can represent this as:
→r=−2^k
Step 2: Use the Work Done Formula
The work done W by a force during a displacement is given by the dot product of the force and displacement vectors:
W=→F⋅→r
Step 3: Substitute the Vectors into the Formula
Now we can substitute the vectors into the work done formula:
W=(12^k)⋅(−2^k)
Step 4: Calculate the Dot Product
The dot product of two vectors can be calculated as follows:
→A⋅→B=|→A||→B|cos(θ)
In this case, since both vectors are in the same direction (along the ^k axis), the angle θ between them is 180 degrees. Thus, cos(180∘)=−1:
W=12×(−2)×(^k⋅^k)=12×(−2)×1=−24 Joules
Step 5: Conclusion
The work done by the force during this displacement is:
W=−24 Joules
This negative sign indicates that the force and displacement are in opposite directions, which is consistent with the physical situation described.
- The force →F is acting in the vertically upward direction with a magnitude of 12 N. We can represent this as:
→F=12^k
- The displacement →r is in the vertically downward direction with a magnitude of 2 m. We can represent this as:
→r=−2^k
The work done W by a force during a displacement is given by the dot product of the force and displacement vectors:
W=→F⋅→r
Now we can substitute the vectors into the work done formula:
W=(12^k)⋅(−2^k)
The dot product of two vectors can be calculated as follows:
→A⋅→B=|→A||→B|cos(θ)
In this case, since both vectors are in the same direction (along the ^k axis), the angle θ between them is 180 degrees. Thus, cos(180∘)=−1:
W=12×(−2)×(^k⋅^k)=12×(−2)×1=−24 Joules
The work done by the force during this displacement is:
W=−24 Joules
Topper's Solved these Questions
- VECTORSBOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Example
40 Videos
- VECTORSBOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - check point 2.1
15 Videos
- VECTORSBOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Single Correct
39 Videos
- UNITS, DIMENSIONS & ERROR ANALYSIS BOOK - DC PANDEY ENGLISHCHAPTER - UNITS, DIMENSIONS & ERROR ANALYSIS EXERCISE - Medical entrances gallery
32 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question
11 Videos
Similar Questions
A force F=(5+2x) acts on a particle in x direction where F is in newtown and x is meter. Find the work done by this force during displacement from x=0 to x=1m.
View SolutionA force F=(5+2x) acts on a particle in x direction where F is in Newtown and x is in meter. Find the work done by this force during displacement from x=0 to x=1m.
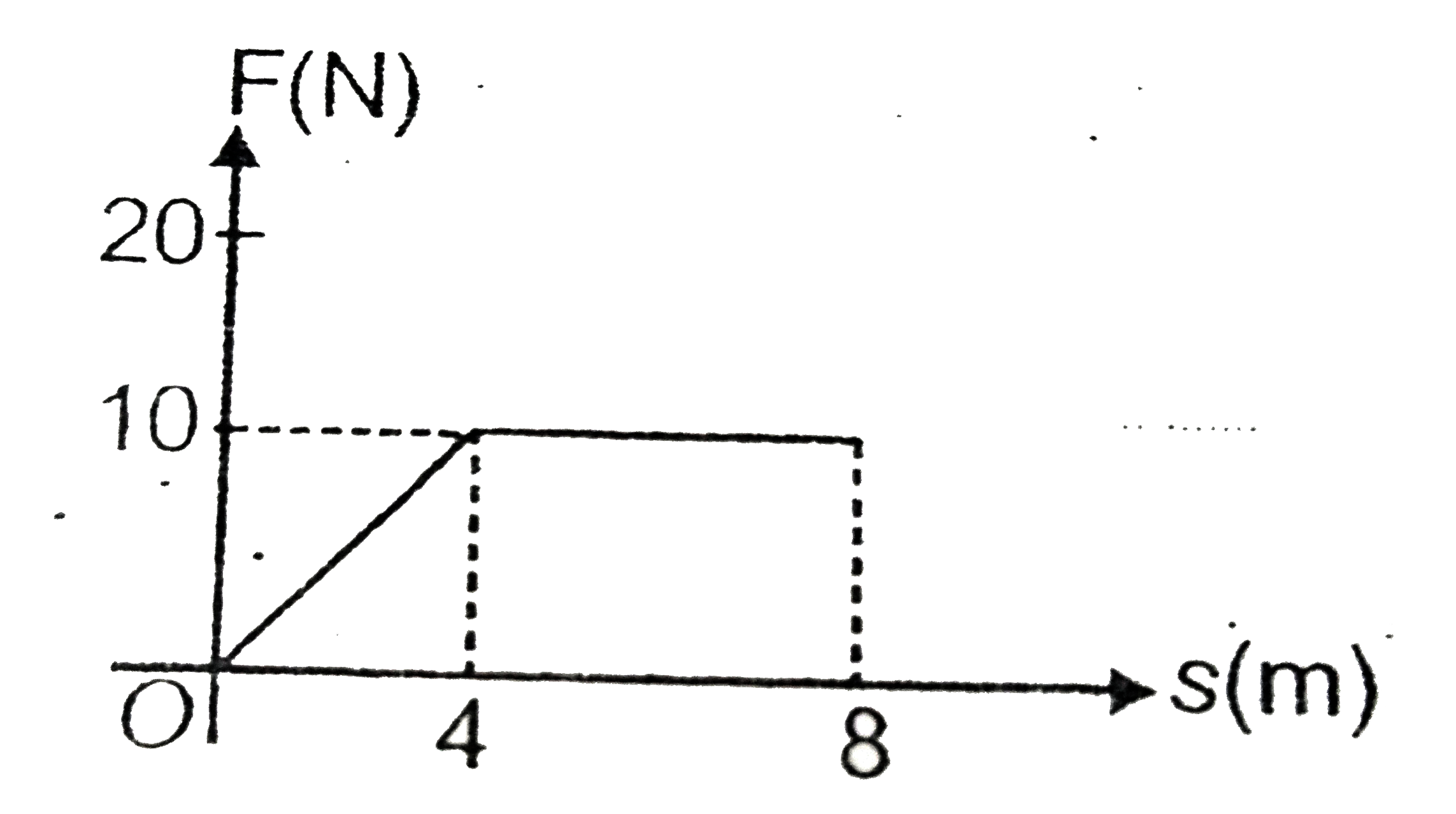
View SolutionForce acting on a particle varies with displacement as shown in figure. Find the total work done by the force.
View SolutionA force F=a+bx acts on a particle in x-direction, where a and b are constants. Find the work done by this force during the displacement from x1 to x2.
View SolutionA particle of mass 20 g is thrown vertically upwards with a speed of 10 m/s. Find the work done by the force of gravity during the time the particle goes up.
View SolutionA force F=(2+x) acts on a particle in x-direction where F is in newton and x in meter. Find the work done by this force during a displacement from 1. 0 m to x = 2.0 m.
View SolutionA force F=(2+x) acts on a particle in x-direction where F is in newton and x in metre. Find the work done by this force during a displacement form 1. 0 m to x = 2.0 m.
View SolutionA force F=a+bx acts on a particle in the x-directioin, where a and b are constants. Find the work done by this force during a displacement form x=0→x=d.
View SolutionA force F=(10+0.50x) acts on a particle in the x direction, where F is in newton and x in meter. Find the work done by this force during a displacement form x=0 to x=2.0m
View SolutionA uniform force of (3ˆi+ˆj) N acts on a particle of mass 2kg. Hence, the particle is displaced from position (2ˆi+ˆk)m to position (4ˆi+3ˆj−ˆk)m. The work done by the force on the particle is
View Solution
