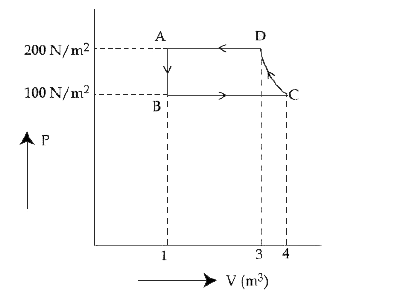
The work done in adiabatic process is given by
nR(T1)−T2γ
nR(T1)−T2γ−1
(nR(T1)−T2)R
γ(T1)−T2Rn
The correct Answer is:B
To find the work done in an adiabatic process, we can follow these steps:
1. Understand the Adiabatic Process: In an adiabatic process, there is no heat exchange with the surroundings. The relationship between pressure (P), volume (V), and temperature (T) for an ideal gas during an adiabatic process is given by the equation PVγ=constant, where γ (gamma) is the heat capacity ratio Cp/Cv.
2. Work Done in an Adiabatic Process: The work done (W) during an adiabatic process can be calculated using the integral:
W=∫V2V1PdV
3. Substituting for Pressure: From the adiabatic condition, we can express pressure in terms of volume:
P=kVγ
where k is a constant.
4. Setting Up the Integral: Substitute P into the work integral:
W=∫V2V1kVγdV
5. Integrating: The integral becomes:
W=k∫V2V1V−γdV=k(V1−γ1−γ)V2V1
6. Evaluating the Integral: Substitute the limits V1 and V2:
W=k(V1−γ2−V1−γ11−γ)
7. Relating to Temperature: Using the ideal gas law PV=nRT, we can express k in terms of temperature:
k=PVγ=nRT⋅Vγ−1
8. Final Expression for Work Done: After substituting and simplifying, we arrive at the expression for work done in an adiabatic process:
W=nR(T1−T2)γ−1
Conclusion:
The work done in an adiabatic process is given by:
W=nR(T1−T2)γ−1
Thus, the correct option is the second one: nR(T1−T2)γ−1.
W=∫V2V1PdV
P=kVγ
where k is a constant.
W=∫V2V1kVγdV
W=k∫V2V1V−γdV=k(V1−γ1−γ)V2V1
W=k(V1−γ2−V1−γ11−γ)
k=PVγ=nRT⋅Vγ−1
W=nR(T1−T2)γ−1
The work done in an adiabatic process is given by:
W=nR(T1−T2)γ−1
Thus, the correct option is the second one: nR(T1−T2)γ−1.
Topper's Solved these Questions
- THERMODYNAMICSBOOK - NCERT FINGERTIPSCHAPTER - THERMODYNAMICSEXERCISE - Heat Engines
4 Videos
- THERMODYNAMICSBOOK - NCERT FINGERTIPSCHAPTER - THERMODYNAMICSEXERCISE - Refrigerators And Heat Pumps
10 Videos
- THERMODYNAMICSBOOK - NCERT FINGERTIPSCHAPTER - THERMODYNAMICSEXERCISE - Thermodynamic State Variables
2 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERT FINGERTIPSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assertion And Reason
10 Videos
- UNITS AND MEASUREMENTSBOOK - NCERT FINGERTIPSCHAPTER - UNITS AND MEASUREMENTSEXERCISE - Assertion And Reason
15 Videos
Similar Questions
Knowledge Check
The work done in an ischoric process is
A0B+ veC(-) veDAny of theseIf a pari of inear equations is consistent then the lines represented by then are
A3 RTBRTC6 RTD2 RTWORK DONE IN ADIABATIC PROCESS
AnR(T1−T2)γBnR(T1−T2)γ−1Cnγ(T1−T2)RDγ(T1−T2)Rn
Derive an expression for work done in an adiabatic process.
View SolutionDefine adiabatic process. Derive an expression for work done during adiabatic process.
View Solutionρ-T equation of a gas in adiabatic process is given by
View Solution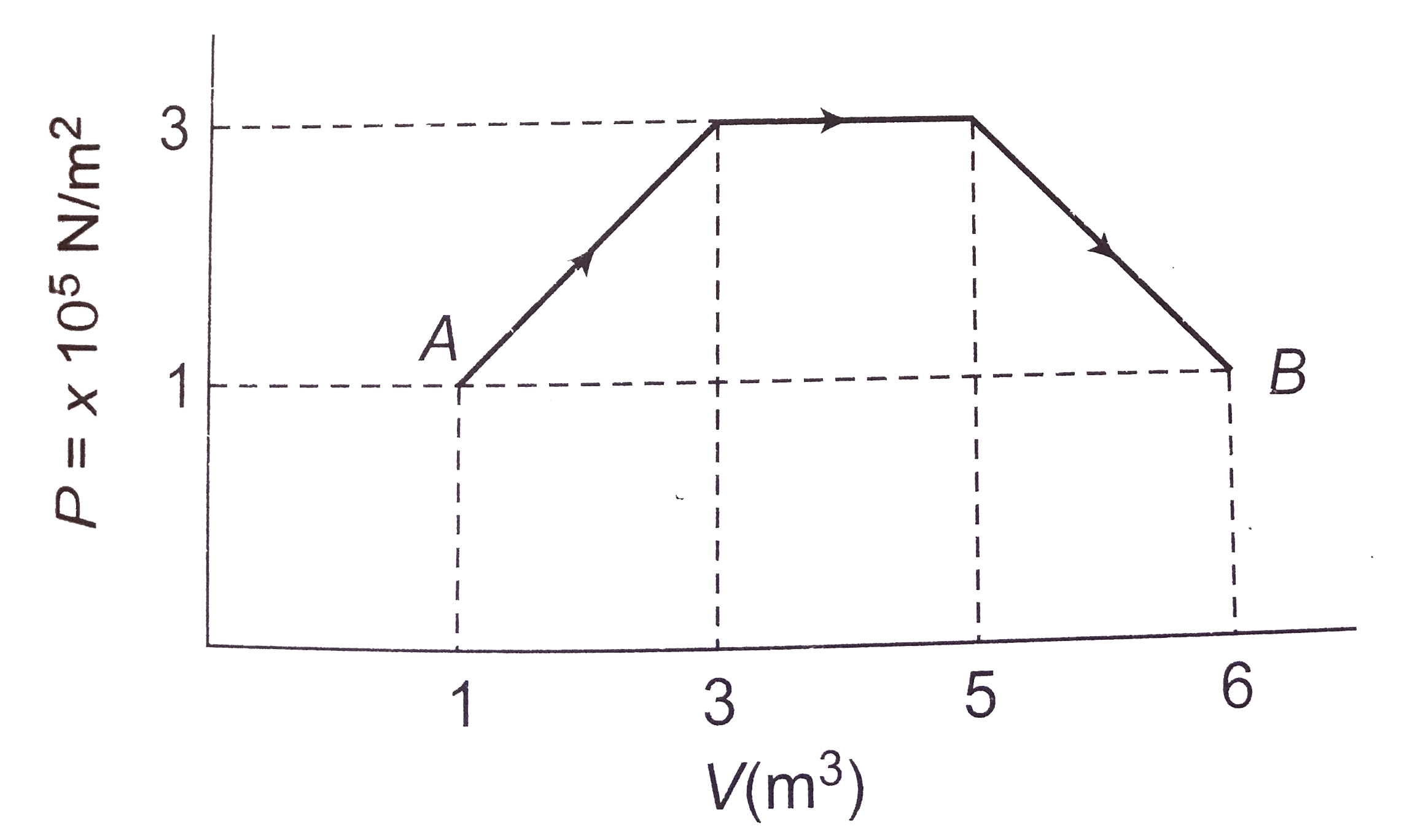
The work done in the process AB is
View SolutionThe work done by 1 mole of ideal gas during an adiabatic process is (are ) given by :
View Solution