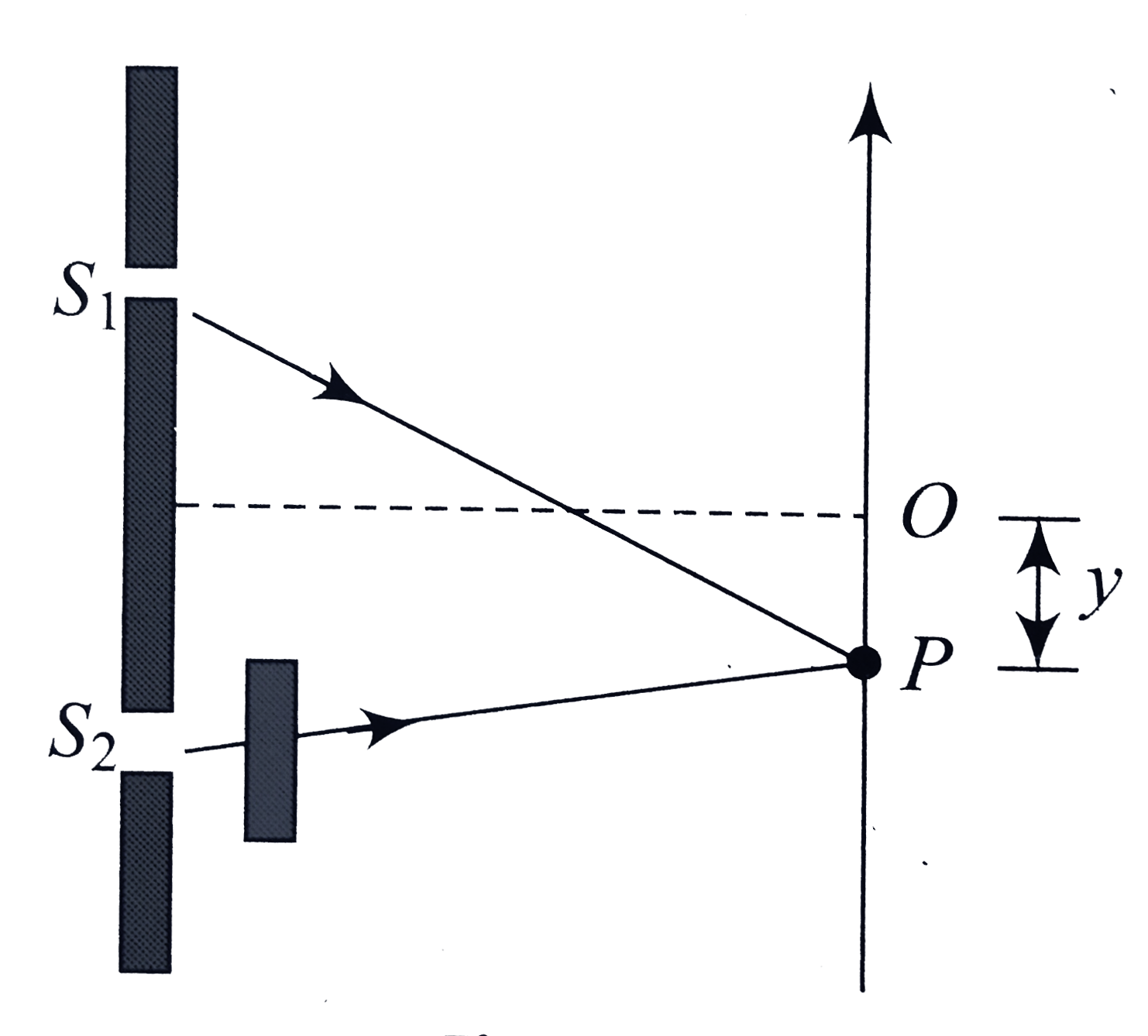
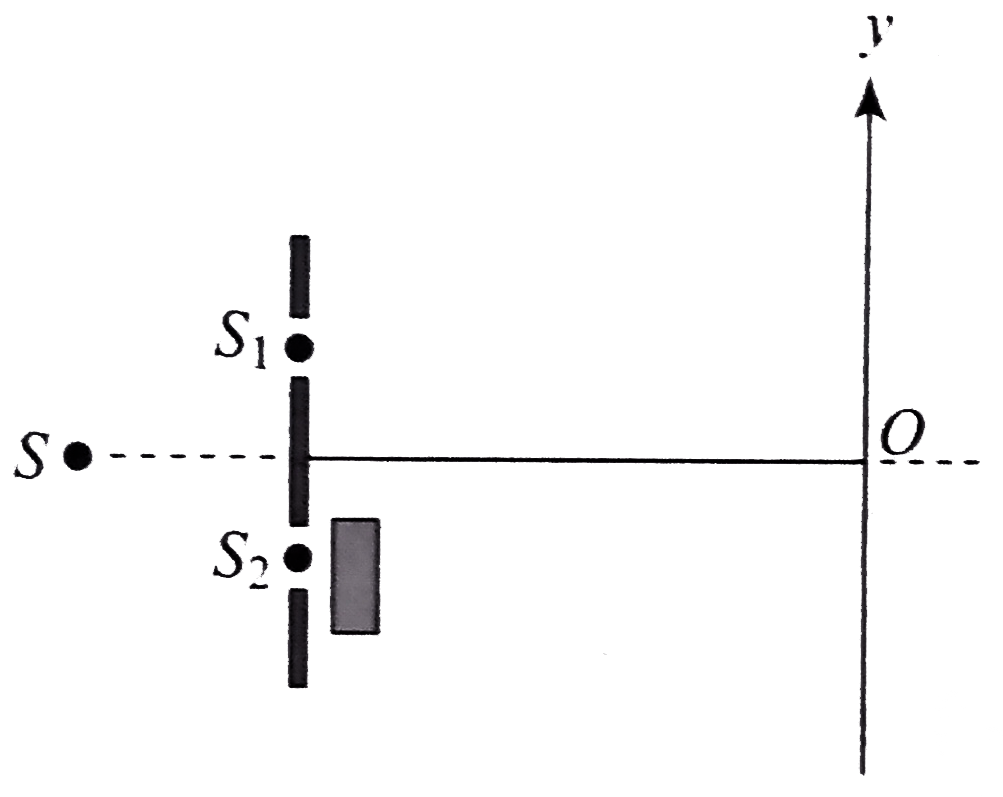
The Young's double-slit experiment is done in a medium of refractive index 4/3. A light of 600 nm wavelength isfalling on the slits having 0.45 mm separation. The lower shift S2 is covered by a thin glass sheet of refractive index. 1.5. The interference pattern is observed on a screen placed 1.5 m from the slits as shown in Figure
a. Find the location of central maximum (bright fringe with zero path difference) on the y-axis.
b. Find the light intensity of point O relative to the maximum fringe intensity.
c. Now , if 600 nm light is replaced by white light of range 400 - 700 nm, find the wavelengths of the light that from maxima exaclty at point O.
(All wavelength in the problem are for the given medium of refractive index 4/3 Ignoe dispersion.)

Given λnm=6×10−7m,d=0.45mm=0.45×10−3m,D=1.5. Thickness of glass sheet,
t=10.4μm=10.4×10−6m.
Refractive index of glass sheet, μg=1.5.
a. Let central maximum is obtained at a distance y below point O.Then,
Δx1=S1P−S2P=ydD
Path difference due to glass sheet,
Δx2=(μgμm−1)t
New path diffenence will be zero when
Δx1=Δx2
⇒ydd=(μgμm−1)t
⇒y=(μgμm−1)tDd
Subsituting the value, we have
y=(μgμm−1)tDd
or we can say y=4.33mm.
a. At O, Δx1=0 and Δx(2)=(μgμm−1)t
∴ Net path difference Δx=Δx2
Corresponding phase difference, Detlaϕ or simply
ϕ=2πλΔx.
Substituting the values, we have
ϕ=2π6×10−7(1.54/3−1)(10.4×10−6)=(133)π
Now,
I(ϕ)=Imaxcos2(ϕ2)
I=Imaxcos2(13π6)
=34Imax
At O, path difference is Δx=Δx2=(μgμm−1)t
For maximum intensity at O,
Δx=nλ (here n=1,2,3,...)
λ=Δx1,Δx2,Δx3,.... and so on
Δx=(1.54/3−1)(10.4×10−6m)
=(1.54/3−1)(10.4×10−3nm
=1300nm
Maximum intensity will be corresponding to
λ1300nm,13002nm,13003nm,13004nm,...
=1300nm,650nm,433.33nm,325nm,...
The wavelength in the range 400 to 700 nm are 650 nm and 433.33 nm.
Topper's Solved these Questions
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Exercise 2.1
12 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - Exercise 2.2
22 Videos
- WAVE OPTICSBOOK - CENGAGE PHYSICSCHAPTER - WAVE OPTICSEXERCISE - QUESTION BANK
37 Videos
- THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - THERMODYNAMICSEXERCISE - QUESTION BANK
34 Videos
- WAVESBOOK - CENGAGE PHYSICSCHAPTER - WAVESEXERCISE - QUESTION BANK
38 Videos
Similar Questions
The young's double slit experiment is done in a medium of refractive index 4/3.A light of 600nmwavelength is falling on the slits having 0.45 mm separation .The lower slit S2 is covered by a thin glass sheet of thickness 10.4μm and refractive index1.5.the intereference pattern is observed ona screen placed 1.5m from the slits are shown
(a) Find the location of the central maximum (bright fringe with zero path difference)on the y-axis.
(b) Find the light intensity at point Orelative to the maximum fringe intensity.
(c )Now,if 600nmlight is replaced by white light of range 400 to700 nm find the wavelength of the light that from maxima exactly point O.[All wavelengths in this problem are for the given medium of refractive index 4/3 .Ignore dispersion]
View SolutionYoung’s double slit experiment is done in a medium of refractive index 4/3. Light of 600 nm wavelength is falling on the slits having 0.45 pm separation. The lower slit S2 is covered by a thin glass sheet of thickness 10.4 pm and refractive index 1.5. The interference pattern is observed on a screen placed 1.5 m from the slits as shown.
(a) Find the location of central maxima (bright fringe with zero I t y path difference) on the y-axis.
(b) Find the light intensity at point O relative to the maximum fringe intensity.
(c) Now, if 600 nm light is replaced by white light of range 400 to 700 nm, find the wavelengths of the light that from maxima exactly at point O[All wavelengths in this problem are for the given medium of refractive index 43. Ignore dispersions.]
View Solution
Knowledge Check
The young's slit experiment is done in a medium of refractive index 4/3 .A light of 600 nm wavelength is falling on the slits having 0.45 mm separation . The lower slit S2 is covered by a thin galss sheet of thickness 10.4 μm and r3efractive index 1.5 .The interferecnce pattern is observed on a screen placed 1.5 m form the slits as shown in figure .Find the light intensity at point O relative to the maximum fringle intensity
(Given:cos3.4=√0.75
 A14B12C34D0
A14B12C34D0A YDSE is performed in a medium of refractive index 4/3, A light of 600 nm wavelength is falling on the slits having 0.45 nm separation . The lower slit S2 is covered b a thin glass plate of thickness 10.4 mm and refractive index 1.5. The interference pattern is observed on a screen placed 1.5 m from the slits as shown in figure. (All the wavelengths in this problem are for the given medium of refractive index 4/3, ignore absorption.)

Find the light intensity at point O relative t maximum fringe intensity.A14ImaxB54ImaxC12ImaxD34ImaxA YDSE is performed in a medium of refractive index 4/3, A light of 600 nm wavelength is falling on the slits having 0.45 nm separation . The lower slit S2 is covered b a thin glass plate of thickness 10.4 mm and refractive index 1.5. The interference pattern is observed on a screen placed 1.5 m from the slits as shown in figure. (All the wavelengths in this problem are for the given medium of refractive index 4/3, ignore absorption.)
The location of the central maximum (bright fringe with zero path difference) on the y-axis will beA2.33 mmB4.33 mmC6.33 mmD4.43 mm
A YDSE is performed in a medium of refractive index 4/3, A light of 600 nm wavelength is falling on the slits having 0.45 nm separation . The lower slit S2 is covered b a thin glass plate of thickness 10.4 mm and refractive index 1.5. The interference pattern is observed on a screen placed 1.5 m from the slits as shown in figure. (All the wavelengths in this problem are for the given medium of refractive index 4/3, ignore absorption.)

Find the light intensity at point O relative t maximum fringe intensity.
View SolutionA YDSE is performed in a medium of refractive index 4/3, A light of 600 nm wavelength is falling on the slits having 0.45 nm separation . The lower slit S2 is covered b a thin glass plate of thickness 10.4 mm and refractive index 1.5. The interference pattern is observed on a screen placed 1.5 m from the slits as shown in figure. (All the wavelengths in this problem are for the given medium of refractive index 4/3, ignore absorption.)

The location of the central maximum (bright fringe with zero path difference) on the y-axis will be
View SolutionIn YDSE's experiment performed in a medium of refractive index (4/3), a light of 60 nm wavelength is falling ono the slits having 0.45 mm separation.t he lower slit S2 is covered by a thin glass sheet of thickness 10.4μm and refractive index 1.5 the interference pattern is observed on a screen palced 1.5m from the slits as shown int hef ignore dispersion.
Q. If white light of range 400-700 nm has replaced 600 nm light, one of the wavelengths of light that forms maxima exactly at point O wll be:

View SolutionIn YDSE's experiment performed in a medium of refractive index (4/3), a light of 60 nm wavelength is falling ono the slits having 0.45 mm separation.t he lower slit S2 is covered by a thin glass sheet of thickness 10.4μm and refractive index 1.5 the interference pattern is observed on a screen palced 1.5m from the slits as shown int hef ignore dispersion.
Q. If white light of range 400-700 nm has replaced 600 nm light, one of the wavelengths of light that forms maxima exactly at point O wll be:

View SolutionA YDSE is performed in a medium of refractive index 4/3, A light of 600 nm wavelength is falling on the slits having 0.45 nm separation . The lower slit S2 is covered b a thin glass plate of thickness 10.4 mm and refractive index 1.5. The interference pattern is observed on a screen placed 1.5 m from the slits as shown in figure. (All the wavelengths in this problem are for the given medium of refractive index 4/3, ignore absorption.)

Now, if 600 nm, find the wavelength of the ligth that forms maximum exactly at point O.
View Solution
