Theposition vector of a moving particle at time t is r=3ˆi+4tˆj−tˆk Its displacement during the time interval t=1 s to t=3 s is
ˆj−ˆk
3ˆi+4ˆj−ˆk
9ˆi+36ˆj−27ˆk
None of the above
The correct Answer is:D
(d) Displacement,S=rf−ri=r3−r1
where rfandri is the final and initial position vector of a particle during the time intervalt=1s to t=3s
∴r3−r1(3ˆi+12ˆj−3ˆj)−(3ˆi+4ˆj−ˆk)=8ˆj−2ˆk
Topper's Solved these Questions
Similar Questions
Knowledge Check
The position vector of a moving particle at seconds in given by →r=3ˆi+4t2ˆj−t3ˆk.Its displacement during an interval of 1s to 3s is
Aˆj−ˆkB3ˆi+4ˆj−ˆkC9ˆi+36ˆj−27ˆkD32ˆj−26ˆkA particle moves in x-y plane. The position vector of particle at any time t is →r={(2t)ˆi+(2t2)ˆj} m. The rate of change of θ at time t = 2 s (where θ is the angle which its velocity vector makes with positive x-axis) is
A217rad s−1B114rad s−1C47rad s−1D65rad s−1The position vector of a particle is given by →r=(3t2ˆi+4t2ˆj+7ˆk)m at a given time t.The net displacement of the particle after 10s is
A500mB400mC300mD700m
Calculate impulse of force →F=(3t2ˆi−(2t−1)ˆj+2ˆk)N over the time interval from t=1s to t=3s.
View SolutionA particle moves along the X-axis. Its X-coordinate varies with time according to the expression x=4t+2r2, where x is in meters and t is in seconds. The position-time graph for this motion is shown in the figures previously. Note that the particle moves in the negative X-direction for the first second of motion, is at rest at the moment t=1s, and then heads back in the positive X-direction for t>1s.
Find the displacement of the particle in the time interval t=1sto t=3s.
View SolutionA particle moves along the X-axis. Its X-coordinate varies with time according to the expression x=4t+2r2, where x is in meters and t is in seconds. The position-time graph for this motion is shown in the figures previously. Note that the particle moves in the negative X-direction for the first second of motion, is at rest at the moment t=1s, and then heads back in the positive X-direction for t>1s.
Find the displacement of the particle in the time interval t=0 s to t=1 s.
View SolutionThe position of a particle moving along x-axis varies eith time t as x=4t−t2+1. Find the time interval(s) during which the particle is moving along positive x-direction.
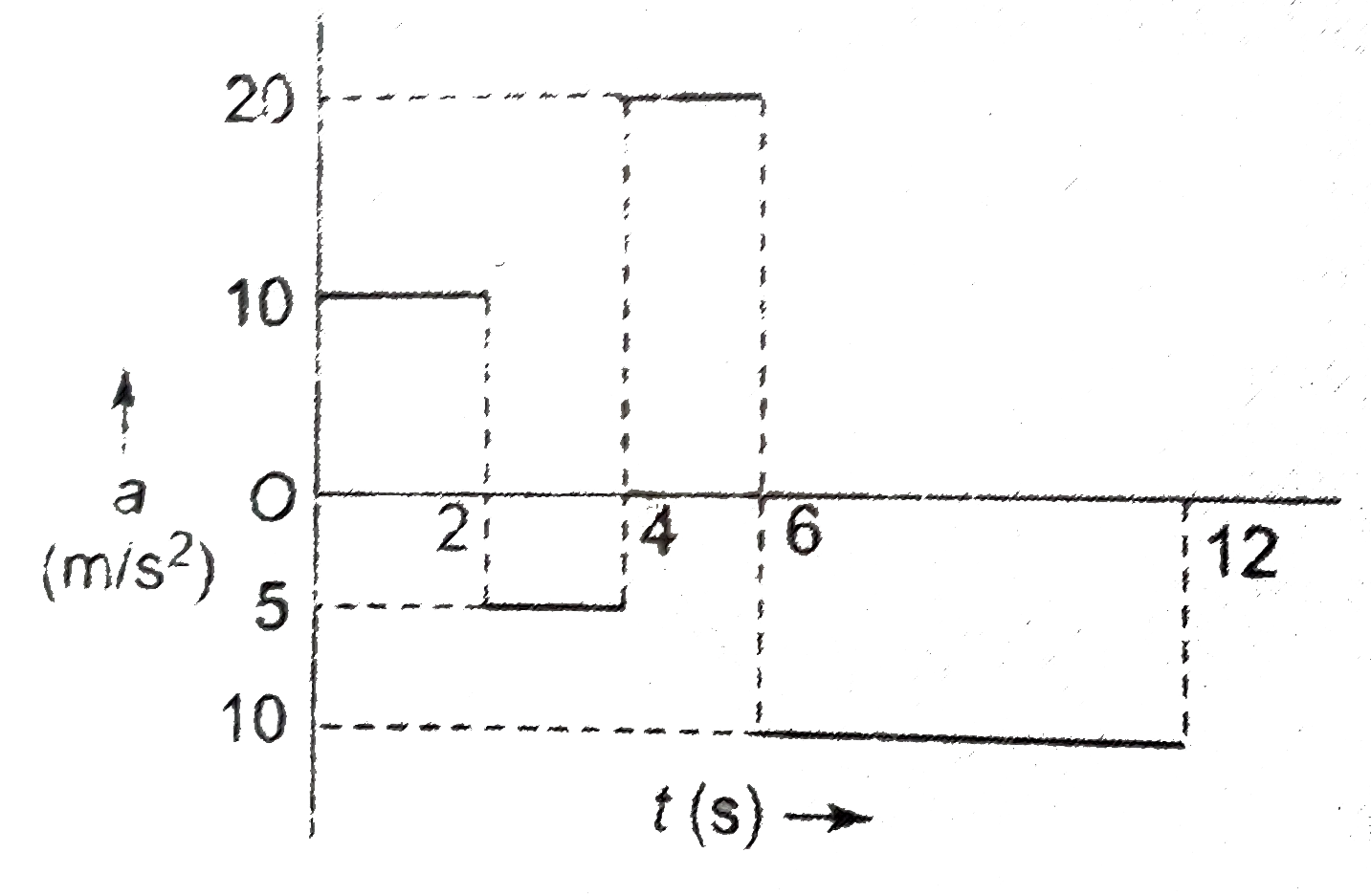
View SolutionA particle is moving along the x-axis. Consider it’s a-t graph. If initial velocity is 10 m//s, sketch the v-t graph and calculate the displacement in the time interval t=0 to 12 s.
View Solution