A particle moves along the X-axis. Its X-coordinate varies with time according to the expression x=4t+2r2, where x is in meters and t is in seconds. The position-time graph for this motion is shown in the figures previously. Note that the particle moves in the negative X-direction for the first second of motion, is at rest at the moment t=1s, and then heads back in the positive X-direction for t>1s.
Find the displacement of the particle in the time interval t=1sto t=3s.
Displacement Δx=xf−xi
=[−4(3)+2(3)2]−[−4(1)+2(1)2]
=8m
Topper's Solved these Questions
- DESCRIPTION OF MOTIONBOOK - CENGAGE PHYSICSCHAPTER - DESCRIPTION OF MOTIONEXERCISE - CONSOLIDATED EXERCISE (MATCH THE COLUMNS)
3 Videos
- DESCRIPTION OF MOTIONBOOK - CENGAGE PHYSICSCHAPTER - DESCRIPTION OF MOTIONEXERCISE - CONSOLIDATED EXERCISE (MULTIPLE-CHOICE QUESTIONS WITH ONE CORRECT ANSWER)
30 Videos
- DESCRIPTION OF MOTIONBOOK - CENGAGE PHYSICSCHAPTER - DESCRIPTION OF MOTIONEXERCISE - MANDATORY EXERCISE (EXERCISE SET - III)
12 Videos
- ELASTICITYBOOK - CENGAGE PHYSICSCHAPTER - ELASTICITYEXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES
10 Videos
Similar Questions
A particle moves along the X-axis. Its X-coordinate varies with time according to the expression x=4t+2r2, where x is in meters and t is in seconds. The position-time graph for this motion is shown in the figures previously. Note that the particle moves in the negative X-direction for the first second of motion, is at rest at the moment t=1s, and then heads back in the positive X-direction for t>1s.
What is the average velocity of the particle in the time interval t=1s to t=3s?
View SolutionA particle moves along the X-axis. Its X-coordinate varies with time according to the expression x=4t+2r2, where x is in metres and t is in seconds. The position-time graph for this motion is shown in the figures previously. Note that the particle moves in the negative X-direction for the first second of motion, is at rest at the moment t=1s, and then heads back in the positive X-direction for t>1s.
What is the average velocity of the particle in the time interval t=0 s to t=1 s?
View Solution
Knowledge Check
A particle moves along the x-axis such that its co-ordinate (x) varies with time (t), according to the expression x=2−5t+6t2, where x is in metres and t is in seconds. The initial velocity of the particle is :–
A−5m/sB−3m/sC6m/sD2m/sA particle moves along X-axis in such a way that its coordinate X varies with time t according to the equation x=(2−5t+6t2)m. The initial velocity of the particle is
A−5m/sB6m/sC−3m/sD3m/sA particle moves along x - axis in such a way that its x - co - ordinate varies with time according to the equation x=4−2t+t2. The speed of the particle will vary with time as
A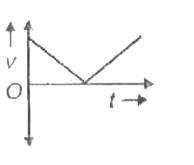 B
B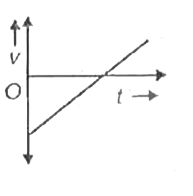 C
C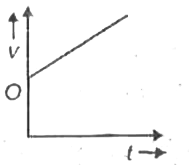 D
D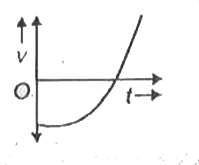
A particle moves along the X-axis. Its X-coordinate varies with time according to the expression x=4t+2r2, where x is in meters and t is in seconds. The position-time graph for this motion is shown in the figures previously. Note that the particle moves in the negative X-direction for the first second of motion, is at rest at the moment t=1s, and then heads back in the positive X-direction for t>1s.
Find the instantaneous velocity of the particle at t=2.5s.
View SolutionA particle is moving along x-axis. Its X-coordinate varies with time as, X=2t2+4t−6 Here, X is in meters and t in seconds. Find average velocity between the time interval t=0→t=2s.
View SolutionA particle is moving along x-axis. Its X-coordinate varies with time as, X=2t2+4t−6 Here, X is in metres and t in seconds. Find average velocity between the time interval t=0→t=2s.
View SolutionA particle moves along X-axis in such a way that its coordinate X varies with time t according to the equation x=(2−5t+6t2)m. The initial velocity of the particle is
View SolutionA particle moves along x - axis in such a way that its x - co - ordinate varies with time according to the equation x=4−2t+t2. The speed of the particle will vary with time as
View Solution
