There are three thermometers one in contact with the skin of the man other in between the vest and the shirt and third in between the shirt and coat. The readings of the thermomenters are 30∘C,25∘C and 22∘C, respectively. If the vest and the shirt are of the same thickness, the ratio of their thermal conductivities is
9:25
25:9
5:3
3:5
The correct Answer is:D
To solve the problem, we need to determine the ratio of the thermal conductivities of the vest and shirt based on the temperature readings from the thermometers. Let's break it down step by step.
Step 1: Understand the Temperature Readings
We have three temperature readings:
- T1=30∘C (skin temperature)
- T2=25∘C (temperature between the vest and shirt)
- T3=22∘C (temperature between the shirt and coat)
Step 2: Calculate the Temperature Differences
We need to find the temperature differences for the two layers:
- For the vest (between skin and vest):
ΔT1=T1−T2=30∘C−25∘C=5∘C
- For the shirt (between vest and coat):
ΔT2=T2−T3=25∘C−22∘C=3∘C
Step 3: Apply the Heat Transfer Equation
In a steady state, the heat transfer through both layers must be equal. The heat transfer Q through a material can be expressed as:
Q=K⋅A⋅ΔTL
Where:
- K is the thermal conductivity,
- A is the area,
- ΔT is the temperature difference,
- L is the thickness of the material.
Since the thickness L and area A are the same for both layers, we can simplify the equation for both layers:
K1⋅ΔT1=K2⋅ΔT2
Step 4: Substitute the Values
Substituting the temperature differences we calculated:
K1⋅5=K2⋅3
Step 5: Rearranging for the Ratio
Rearranging the equation to find the ratio of thermal conductivities:
K1K2=35
Conclusion
The ratio of the thermal conductivities of the vest and shirt is:
K1K2=35
We have three temperature readings:
- T1=30∘C (skin temperature)
- T2=25∘C (temperature between the vest and shirt)
- T3=22∘C (temperature between the shirt and coat)
We need to find the temperature differences for the two layers:
- For the vest (between skin and vest):
ΔT1=T1−T2=30∘C−25∘C=5∘C
- For the shirt (between vest and coat):
ΔT2=T2−T3=25∘C−22∘C=3∘C
In a steady state, the heat transfer through both layers must be equal. The heat transfer Q through a material can be expressed as:
Q=K⋅A⋅ΔTL
Where:
- K is the thermal conductivity,
- A is the area,
- ΔT is the temperature difference,
- L is the thickness of the material.
K1⋅ΔT1=K2⋅ΔT2
Substituting the temperature differences we calculated:
K1⋅5=K2⋅3
Rearranging the equation to find the ratio of thermal conductivities:
K1K2=35
The ratio of the thermal conductivities of the vest and shirt is:
K1K2=35
Topper's Solved these Questions
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Multiple Correct
25 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Comprehension
30 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Subjective
25 Videos
- BASIC MATHEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.6
20 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
Two walls of thickness in the ratio 1:3 and thermal conductivities in the ratio 3:2 form a composite wall of a building. If the free surfaces of the wall be at temperatures 30∘C and 20∘C, respectively, what is the temperature of the interface?
View SolutionA capacitor is composed of three parallel conducting plates. All three plates are of the same area A. The first pair of plates are kept a distance d1 apart, and the space between them is filled with a medium of a dielectric K1 . The corresponding data of the second pair are d2 and K2, respectively. The middle plate is connected to the positive terminal of a constant voltage source V and the external plates are connected the other terminal of V.

(a) Find the capacitance of the system .
(b) What is the surface charge density on the middle plate ?
(c) Compute the energy density in the medium K1
View SolutionAssume that the thermal conductivity of copper is twice that of aluminium and four times that of brass. Three metal rods made of copper, aluminium and brass are each 15 cm long and 2 cm in diameter. These rods are placed end to end, with aluminium between the other two. The free ends of the copper and brass rods are maintained at 100∘C and 0∘C respectively. The system is allowed to reach the steady state condition. Assume there is no loss of heat anywhere.
When steady state condition is reached everywhere, which of the following statement is true?
View SolutionAssume that the thermal conductivity of copper is twice that of aluminium and four times that of brass. Three metal rods made of copper, aluminium and brass are each 15 cm long and 2 cm in diameter. These rods are placed end to end, with aluminium between the other two. The free ends of the copper and brass rods are maintained at 100∘C and 0∘C respectively. The system is allowed to reach the steady state condition. Assume there is no loss of heat anywhere.
When steady state condition is reached everywhere, which of the following statement is true?
View SolutionThree rods A, B and C of the same length and same cross-sectional area are joined as shown. Their thermal conductivities are in the ratio 1:2:3/2. If the open ends of A and C are at 200∘C and 18∘C, respectively, then the temperature at the junction of A at steady state is
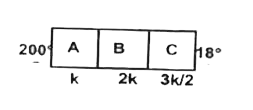
View SolutionTwo plates of equal areas are placed in contact wih each other. Their thickness are 2.0 cm and 5.0 cm respectively. The temperature of the external surface of the first plate is −20∘C and that of the external surface of the second plate is 20∘C. What will be the temperature of the current surface if the plates (i) are of the same material, (ii) have thermal conductivities in the ratio 2:5.
View SolutionOne end of a uniform brass rod 20 cm long and 10cm2 cross-sectional area is kept at 100∘C. The other end is in perfect thermal contact with another rod of identical cross-section and length 10 cm. The free end of this rod is kept in melting ice and when the steady state has been reached, it is found that 360 g of ice melts per hour. Calculate the thermal conductivity of the rod, given that the thermal conductivity of brass is 0.25cal/scm∘CandL=80cal/g.
View SolutionThree rods of identical cross - section and length are made of three different material of thermal conductivity k1,k2 and k3 respectively. They are joined together at their ends to make a long rod (See figure). One end of the long rod is maintained at 100∘C and the other at 0∘C ( See figure ). If the joints of the rod are at 70∘C and 20∘C in steady state and there is no loss of energy form the surface of the rod, the correct relationship between k1,k2 and k3 is
View SolutionThree metal rods made of copper, aluminium and brass, each 20cm long 4cm in diameter, are placed end to end with aluminium between the other two. The free ends of copper and brass are maintained at 100 and 0∘C respectively. Assume that the thermal conductivity of copper is twice that of aluminium and four times that of brass. The approximately equilibrium temperatures of the copper-aluminiu and aluminium-brass junctions are respectively.

View SolutionAn electric heater is placed inside a room of total wall area 137m2 to maintain the temperature inside at 20∘C. The outside temperature is −10∘C. The walls are made of three composite materials. The inner most layer is made of wood of thickness 2.5 cm the middle layer is of cement of thickness 1 cm and the exterior layer is of brick of thickness 2.5 cm. Find the power of electric heater assuming that there is no heat losses through the floor and ceiling. The thermal conductivities of wood, cement and brick are 0.125W/m∘−C,1.5W/m∘−Cand1.0W/m∘−C respectively.
View Solution
