Assume that the thermal conductivity of copper is twice that of aluminium and four times that of brass. Three metal rods made of copper, aluminium and brass are each 15 cm long and 2 cm in diameter. These rods are placed end to end, with aluminium between the other two. The free ends of the copper and brass rods are maintained at 100∘C and 0∘C respectively. The system is allowed to reach the steady state condition. Assume there is no loss of heat anywhere.
When steady state condition is reached everywhere, which of the following statement is true?
No heat is transmitted across the copper aluminium or aluminium brass junctions.
More heat is transmitted across the copper aluminium junction than across the aluminium brass junction.
More heat is tranmitted across the aluminium brass junction than the copper aluminium junction.
Equal amount of heat is transmitted at the copper aluminium and aluminium brass junctions.
The correct Answer is:D
To solve the problem, we need to analyze the heat transfer through the three metal rods (copper, aluminum, and brass) when they are placed end to end and subjected to different temperatures at their ends.
1. Identify the Thermal Conductivities:
- Let the thermal conductivity of aluminum be k.
- Therefore, the thermal conductivity of copper will be 2k (twice that of aluminum).
- The thermal conductivity of brass will be k2 (four times less than copper).
2. Understand the Configuration:
- The rods are arranged in the sequence: Copper (100°C) - Aluminum - Brass (0°C).
- Each rod has a length of 15 cm and a diameter of 2 cm.
3. Heat Transfer Rate:
- The rate of heat transfer Q through a rod can be expressed using Fourier's law of heat conduction:
Q=k⋅A⋅ΔTL
where:
- k is the thermal conductivity,
- A is the cross-sectional area,
- ΔT is the temperature difference across the rod,
- L is the length of the rod.
4. Calculate Cross-Sectional Area:
- The cross-sectional area A for a circular rod is given by:
A=π(d2)2=π(1 cm)2=π cm2
5. Steady State Condition:
- In steady state, the rate of heat transfer through each rod must be equal:
Qcopper=Qaluminum=Qbrass
6. Set Up the Equations:
- For copper:
Q=2k⋅π⋅(100−T1)15
- For aluminum:
Q=k⋅π⋅(T1−T2)15
- For brass:
Q=k2⋅π⋅(T2−0)15
7. Equate the Heat Transfer Rates:
- Since Q is the same for all rods, we can set up the following equations:
2k⋅π⋅(100−T1)15=k⋅π⋅(T1−T2)15
k⋅π⋅(T1−T2)15=k2⋅π⋅(T2−0)15
8. Solve for Temperature Differences:
- From the first equation, simplify and solve for T1:
2(100−T1)=T1−T2
200−2T1=T1−T2
3T1−T2=200(1)
- From the second equation, simplify and solve for T2:
2(T1−T2)=T2
2T1−2T2=T2
2T1=3T2(2)
9. Substitute and Solve:
- Substitute equation (2) into equation (1):
3T1−23T1=200
73T1=200
T1=6007≈85.71°C
- Substitute T1 back into equation (2) to find T2:
2T1=3T2⟹2×6007=3T2
T2=120021≈57.14°C
10. Conclusion:
- The steady state temperatures are approximately T1≈85.71°C and T2≈57.14°C.
- Since the heat transfer rate is the same across all junctions, the correct statement is:
Equal amounts of heat are transmitted at the copper-aluminum and aluminum-brass junctions.
- Let the thermal conductivity of aluminum be k.
- Therefore, the thermal conductivity of copper will be 2k (twice that of aluminum).
- The thermal conductivity of brass will be k2 (four times less than copper).
- The rods are arranged in the sequence: Copper (100°C) - Aluminum - Brass (0°C).
- Each rod has a length of 15 cm and a diameter of 2 cm.
- The rate of heat transfer Q through a rod can be expressed using Fourier's law of heat conduction:
Q=k⋅A⋅ΔTL
where:
- k is the thermal conductivity,
- A is the cross-sectional area,
- ΔT is the temperature difference across the rod,
- L is the length of the rod.
- The cross-sectional area A for a circular rod is given by:
A=π(d2)2=π(1 cm)2=π cm2
- In steady state, the rate of heat transfer through each rod must be equal:
Qcopper=Qaluminum=Qbrass
- For copper:
Q=2k⋅π⋅(100−T1)15
- For aluminum:
Q=k⋅π⋅(T1−T2)15
- For brass:
Q=k2⋅π⋅(T2−0)15
- Since Q is the same for all rods, we can set up the following equations:
2k⋅π⋅(100−T1)15=k⋅π⋅(T1−T2)15
k⋅π⋅(T1−T2)15=k2⋅π⋅(T2−0)15
- From the first equation, simplify and solve for T1:
2(100−T1)=T1−T2
200−2T1=T1−T2
3T1−T2=200(1)
2(T1−T2)=T2
2T1−2T2=T2
2T1=3T2(2)
- Substitute equation (2) into equation (1):
3T1−23T1=200
73T1=200
T1=6007≈85.71°C
- Substitute T1 back into equation (2) to find T2:
2T1=3T2⟹2×6007=3T2
T2=120021≈57.14°C
- The steady state temperatures are approximately T1≈85.71°C and T2≈57.14°C.
- Since the heat transfer rate is the same across all junctions, the correct statement is:
Equal amounts of heat are transmitted at the copper-aluminum and aluminum-brass junctions.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Integer8videos
CALORIMETRY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example13videos
CALORIMETRY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Multiple Correct25videos
CALORIMETRY
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.620videos
BASIC MATHEMATICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE1videos
CENTRE OF MASS
Similar Questions
Three metal rods made of copper, aluminium and brass, each 20cm long 4cm in diameter, are placed end to end with aluminium between the other two. The free ends of copper and brass are maintained at 100 and 0∘C respectively. Assume that the thermal conductivity of copper is twice that of aluminium and four times that of brass. The approximately equilibrium temperatures of the copper-aluminiu and aluminium-brass junctions are respectively.
 View Solution
View SolutionTwo ends of a conducting rod of varying cross-section are maintained at 200∘C and 0∘C respectively. In steady state:
 View Solution
View SolutionThe outer faces of a rectangular slab made of equal thickness of iron and brass are maintained at 100∘C and 0∘C respectively. The temperature at the interface is (Thermal conductivity of iron and brass are 0.2 and 0.3 respectively)
View SolutionThe ends of a metre stick are maintain at 100∘C and 0∘C . One end of a rod is maintained 25∘C . Where should its other end be touched on the metre stick so that there is no heat current in the rod in steady state?
View SolutionTwo rods of similar area of cross section and length are joined as shown in the figure. The ratio of their thermal conductivity is 2:3. The free ends are maintained at 100∘C and 0∘C respectivley. THE temperature at junction in steady state is
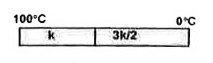 View Solution
View SolutionA copper rod of length 75 cm and an iron rod of length 125cm are joined together end to end . Both are of circular cross section with diameter 2 cm . The free ends of the copper and iron are maintained at 100∘C and0∘C respectively . The surface of the bars are insulated thermally . The temperature of the copper -iron junction is [Thermal conductivity of the copper is 386.4W/m−K and that of iron is 48.46W/m−K].
View SolutionA bar of copper of length 75cm and a bar of steel of length 125cm are joined together end to end. Both are of circular cross section with diameter 2cm. The free ends of the copper and the steel bars are maintained at 100∘C and 0∘C respectively. The curved surface of the bars are thermally insulated. What is the temperature of the copper-steel junction? What is the amount of heat transmitted per unit time across the junction? Thermal conductivity of copper is 386Js−1m−1C−1 and that of steel is 46Js−1m−1C−1
View SolutionIn a steady state of thermal conduction, temperature of the ends A and B of a 20 cm long rod are 100∘C and 0∘C respectively. What will be the temperature of the rod at a point at a distance of 9 cm from the end A of the rod
View SolutionTwo rods of same dimensions, but made of different materials are joined end to end to end with their free end being maintained at 100∘C and 0∘C respectively. The temperature of the junction is 70∘C. Then the temperature of the junction if the rods are inerchanged will be equal to T∘C Find T:
View SolutionThe ends of a copper rod of length 1m and area of cross-section 1cm2 are maintained at 0∘C and 100∘C. At the centre of the rod there is a source of heat of power 25 W. Calculate the temperature gradient in the two halves of the rod in steady state. Thermal conductivity of copper is 400Wm−1K−1.
View Solution

