There are two large identical open tanks as shown in figure. In tanks 1 there is a small hole of cross sectional area A at its base. Tank II has a similar hole, to which a pipe of length h has been connected as shown. The internal cross sectional area of the pipe can be considered to be equal
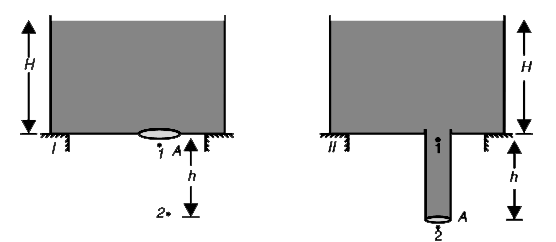
to A. Point 1 marked in both figures, is a point just below the opening in the tank and point 2 marked in both figures, is a point h below point 1 (In fig II, point 2 is just outside the opening in the pipe)
(a) Find the speed of flow at point 2 in both figures.
(b) Find the ratio of speed of flow at point 1 is first the ratio of speed of flow at point 1 is first figure to that in second figure.
(c) Find the difference in pressure at point 1 in both figures.
The correct Answer is:(a) In both figures v2=√2g(H+h)
(b) √HH+h
(c) ρgh
Step by step video, text & image solution for There are two large identical open tanks as shown in figure. In tanks 1 there is a small hole of cross sectional area A at its base. Tank II has a similar hole, to which a pipe of length h has been connected as shown. The internal cross sectional area of the pipe can be considered to be equal to A. Point 1 marked in both figures, is a point just below the opening in the tank and point 2 marked in both figures, is a point h below point 1 (In fig II, point 2 is just outside the opening in the pipe) (a) Find the speed of flow at point 2 in both figures. (b) Find the ratio of speed of flow at point 1 is first the ratio of speed of flow at point 1 is first figure to that in second figure. (c) Find the difference in pressure at point 1 in both figures. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Three rods of same material and of equal cross sectional area and length have been connected together as shown in the figure. The temperature of the junction of the rods approximately is
View SolutionThe water level on a tank is 5m high. There is a hole of 1cm2 cross-section at the bottom of the tank. Find the initial rate with which water will leak through the hole. (g=10ms−2)
View Solution
Knowledge Check
A large cylindrical tank has a hole of area A at its bottom. Water is oured in the tank by a tube of equal cross sectional area A ejecting water at the speed v.
Athe water level in the tank wil keep on rising.Bno water an be stored in the tankCthe water level will rise to a height v22g and then stopDthe water level will oscillate.There are two holes on a water tank as shown in figure. Area of hole 2 is two times that of area of hole 1. Suppose v is the speed of liquid coming out and Q the volume of liquid flowing per second. Then
 AV1=4V2BV1=2V2CQ1=Q2DQ1=2Q2
AV1=4V2BV1=2V2CQ1=Q2DQ1=2Q2Water is filled to height h in a fixed vertical cylinder placed on horizontal surface. At time t=0 a small hole a drilled at a height h/4 from bottom of cylinder as shown. The cross section area of hole is a and the cross-section area of cylinder is A such that A>>a.

The duration of time for which water flows out of hole is.AAa√3h2gBaA√3h2gCAa√2h3gDNone of these
The level of water in a huge tank is 20 m. Nearly at the bottom of the tank, there is a hole of 2 cm? cross section. The rate with which the water will leak through the hole is n×10−3cm. Find the value of n.
View SolutionIn the figure shown cross-section area of holes are same and very small in comparison to area of cross-section of water tank : (tanks are the open from the top) Choose the correct option(s) :

View SolutionA lawn sprinkler has 20 holes, each of cross-sectional area 2.0x10−2cm2, and is connected to a hose pipe of cross sectional area 2.4cm2. If the speed of water in the hose pipe is 1.5ms−1, the speed of water as it emerges from the holes is
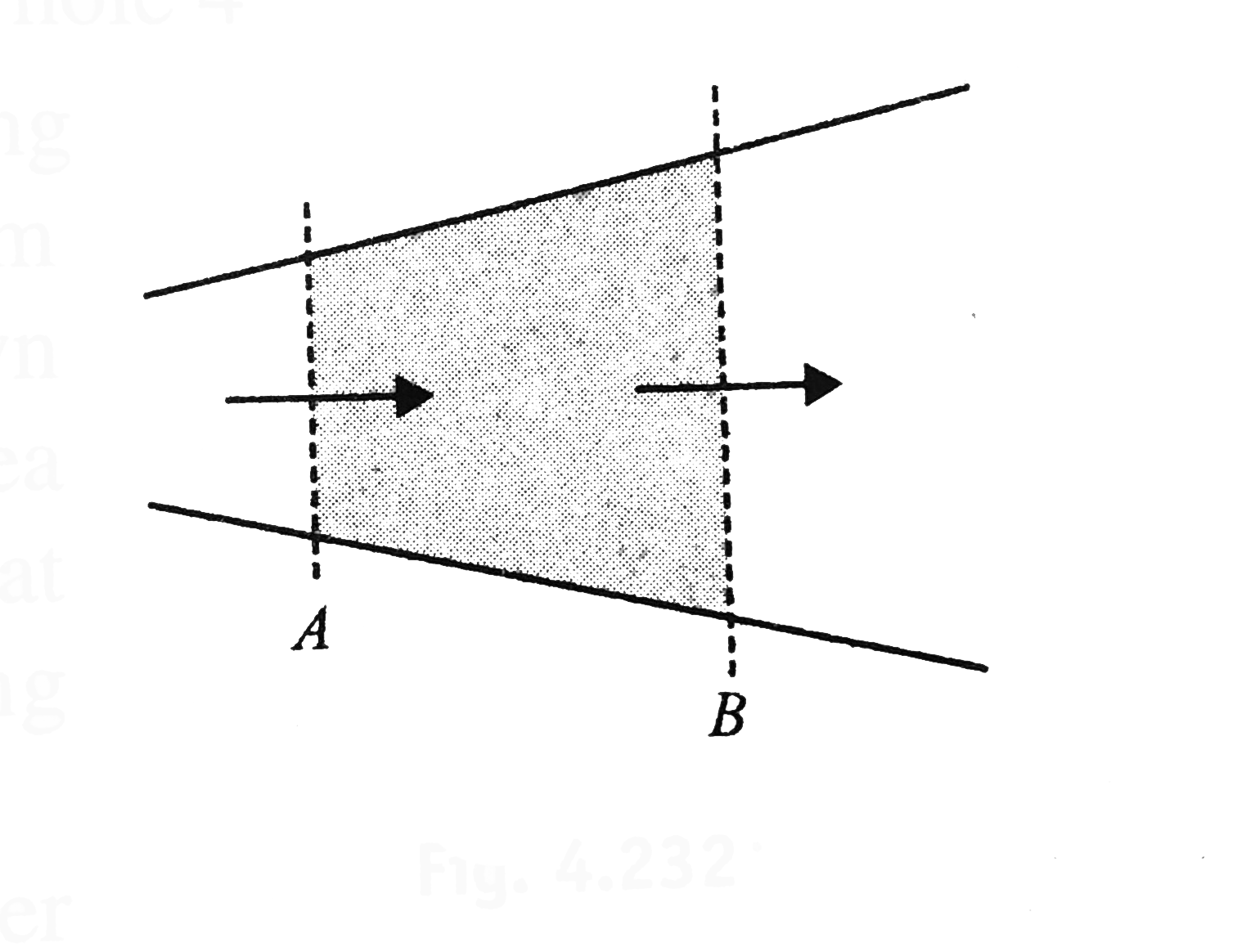
View SolutionA non-viscous liquid is flowing through a non-uniform pipe from section A to section B as shown in the figure. Cross sectional area of the pipe at A is less than that at B. Which of the following statements are correct?
View SolutionPipe A can fill a tank in 20 minutes and Pipe B can empty the same tank in 30 minutes. Find the time taken to fill the empty tank if both pipes are opened together
View Solution
