There exists a long conductor along z-axis carrying a current I0 along positive z-direction. A loop having total resistance R is placed symmetrical about x-axis and y-axes in x-y plane as shown in Fig. potential difference VBA=V is applied. Radii of arcs are a and b, respectively, as shown in the figure.
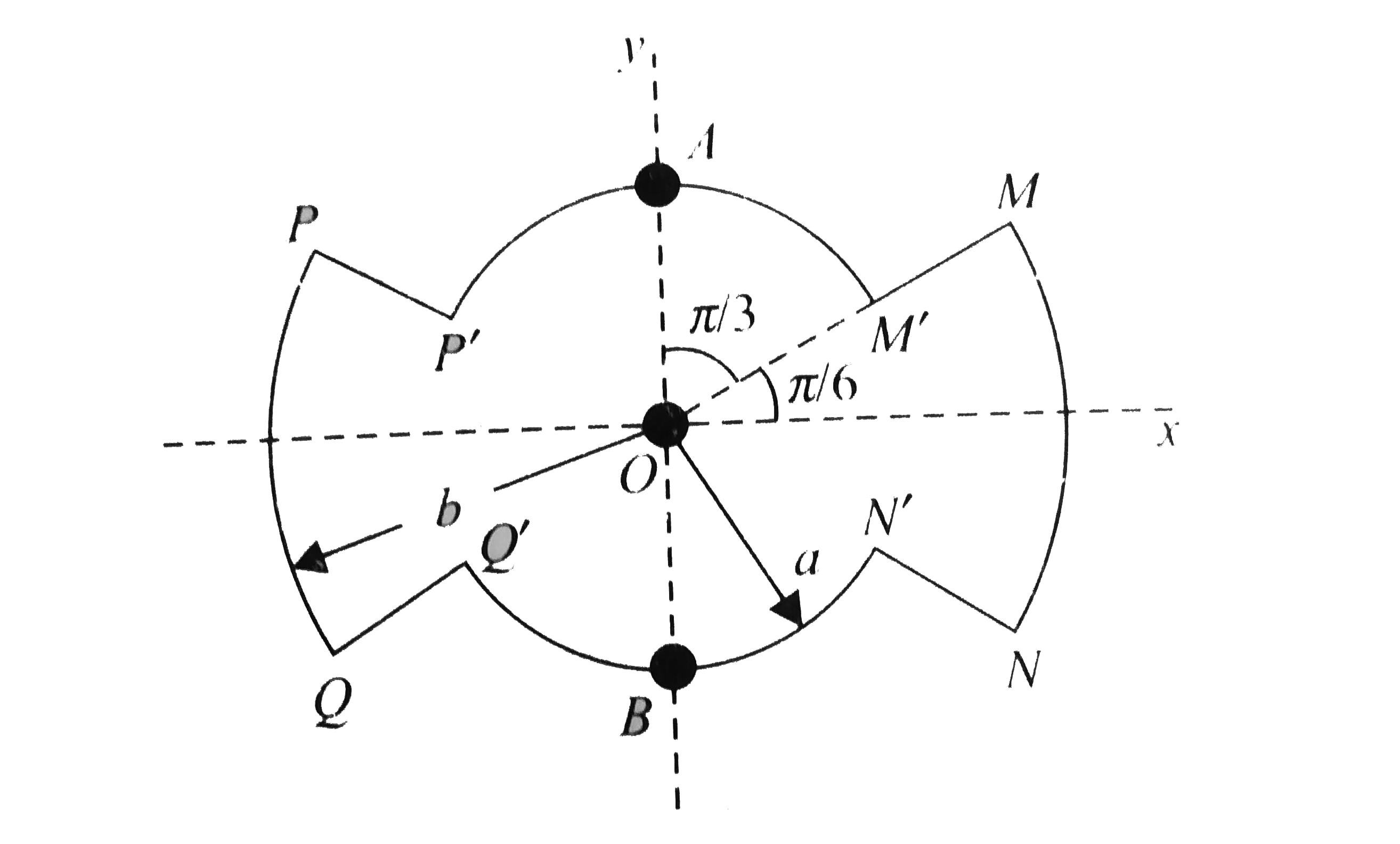
The total torque acting on the loop is nearly
μ0VI0πR(b−a)ˆi
−2μ0VI0πR(b−a)ˆi
μ0VI02πR(b−a)ˆi
none of these
The correct Answer is:B
(b)
Magnetic field produced by the conductor along z-axis will
be parallel to MN. Hence, force on MN is zero.
Current from B to A (through NM or QP):
I=VR/2=2VR
Force due to I0 on N'N and Q'Q will be out of the paper and on
M'M and P'P will be in the paper. This will produce the torque
Torque on M'M (along negative x-axis):
τ=∫ba(μ0I02πrIdr)rsin(π6)=μ0I04πI(b−a)
=μ0I02V4Rπ(b−a)
Total torque =4τ=2μ0I0VπR(b−a) (along negative x-axis.)
Topper's Solved these Questions
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (integer)
7 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Archives (fill In The Blanks)
1 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (assertion-reasioning )
2 Videos
- SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - CENGAGE PHYSICSCHAPTER - SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - QUESTION BANK
12 Videos
- THERMAL PROPERTIES OF MATTERBOOK - CENGAGE PHYSICSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Bank
40 Videos
Similar Questions
A circular loop of radius R=20 cm is placed in a uniform magnetic field B=2T in xy-plane as shown in figure. The loop carries a current i=1.0A in the direction shown in figure. Find the magnitude of torque acting on the loop.

View SolutionA wire loop carrying current I is placed in the x−y plane as shown in the figure. If an external uniform magnetic field →B=Bˆi is switched on, then the torque acting on the loop is
View Solution
Knowledge Check
There exists a long conductor along z-axis carrying a current I0 along positive z-direction. A loop having total resistance R is placed symmetrical about x-axis and y-axes in x-y plane as shown in Fig. potential difference VBA=V is applied. Radii of arcs are a and b, respectively, as shown in the figure.
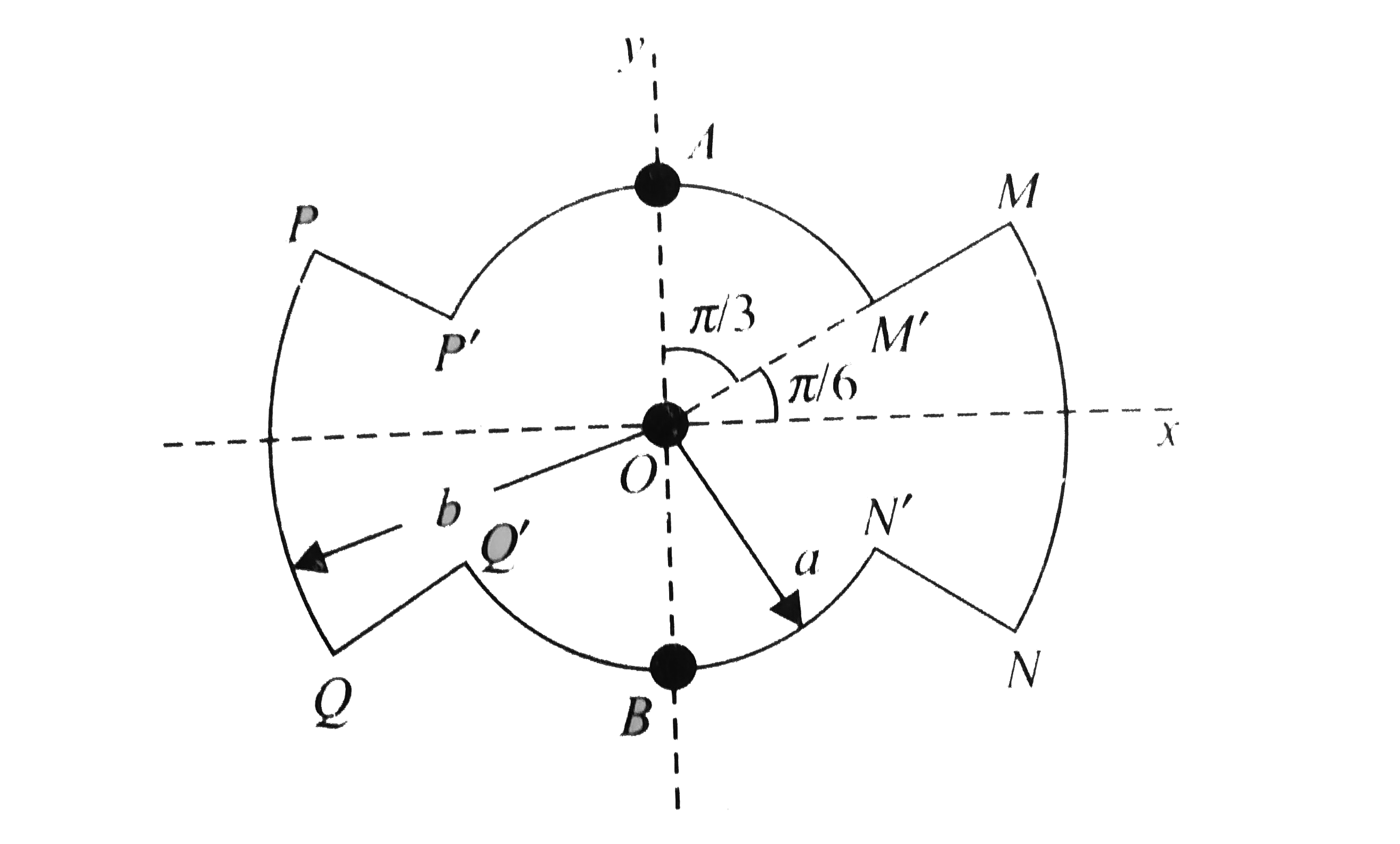
The magnitude of force experienced by the arc MN isAzeroBμ0VI0πRbCμ0VI02πRbDnone of theseA long straight wire along the z−aξs carries a current I in the negative z−direction . The magnetic vector field →B at a point having coordinates (x,y) in the Z=0 plane is
Aμ0I(yˆi)−xˆj2π(x2+y2)Bμ0I(xˆi)+yˆj2π(x2+y2)Cμ0I(xˆj)−yˆi2π(x2+y2)Dμ0I(yxˆi)−yˆj2π(x2+y2)A long straight wire along the z-axis carries a current I in the negative z-direction. The magnetic vector field →B at a point having coordinnates (x, y) in the z = 0 plane is
Aμ0I(yˆi−xˆj)2π(x2+Y2)Bμ0I(xˆi+yˆj)2π(x2+Y2)Cμ0I(xˆj−yˆi)2π(x2+Y2)Dμ0I(xˆi−yˆj)2π(x2+Y2)
A long, straight wire carries a current along the z-axis. One can find two points in the x-y plane such that
View Solution(a) Find the magnetic field at the point O if the wire carrying a current i has the shape shown. The radius of the current part of the wire is R, the linear parts of the wire are very long.
(i)
(ii)
(iii)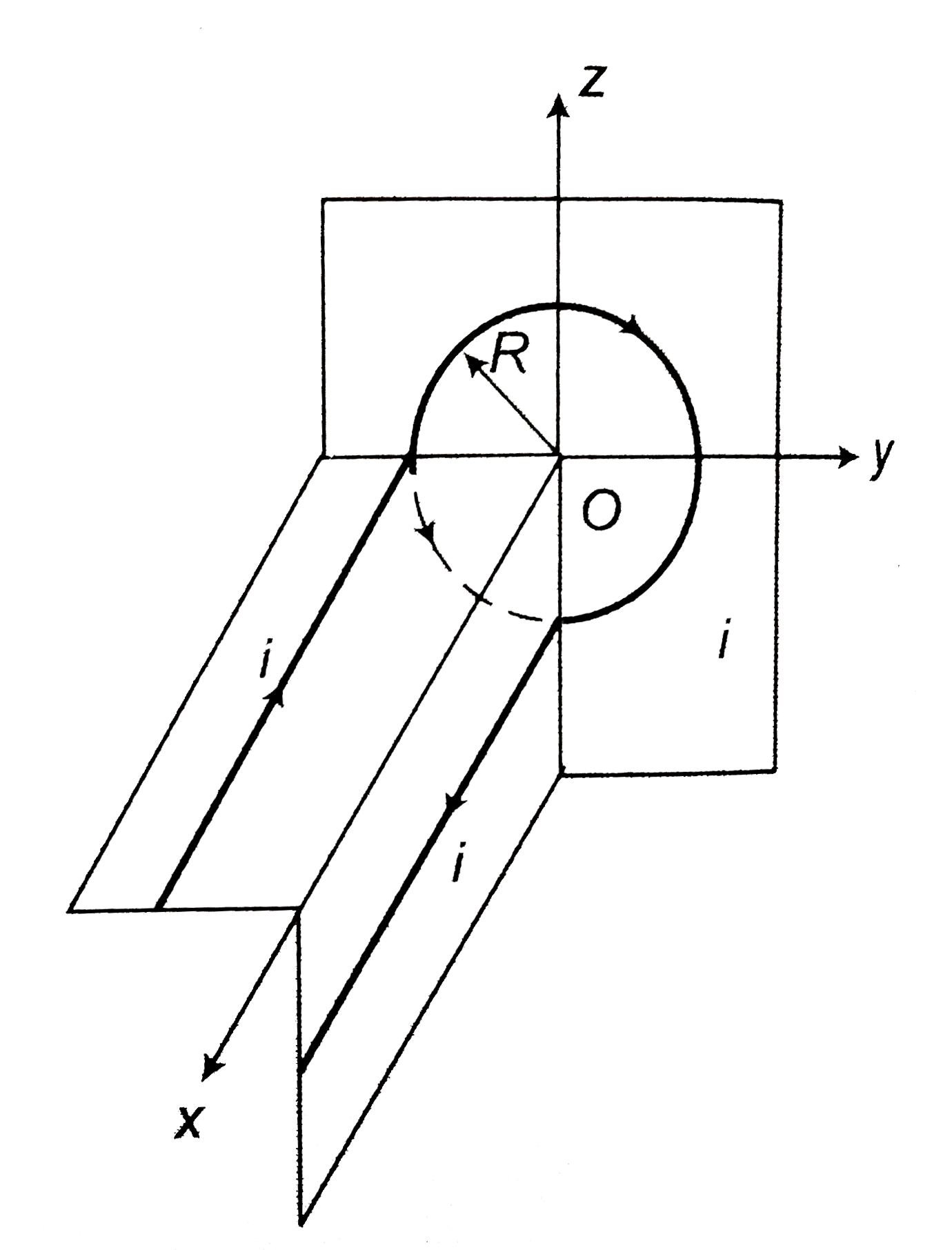
(b) A long straight wire along the z-axis carriers a current i in negative z-direction. Find magnetic field in vector from at a point having co-ordinates (x,y) on z=0 plane.
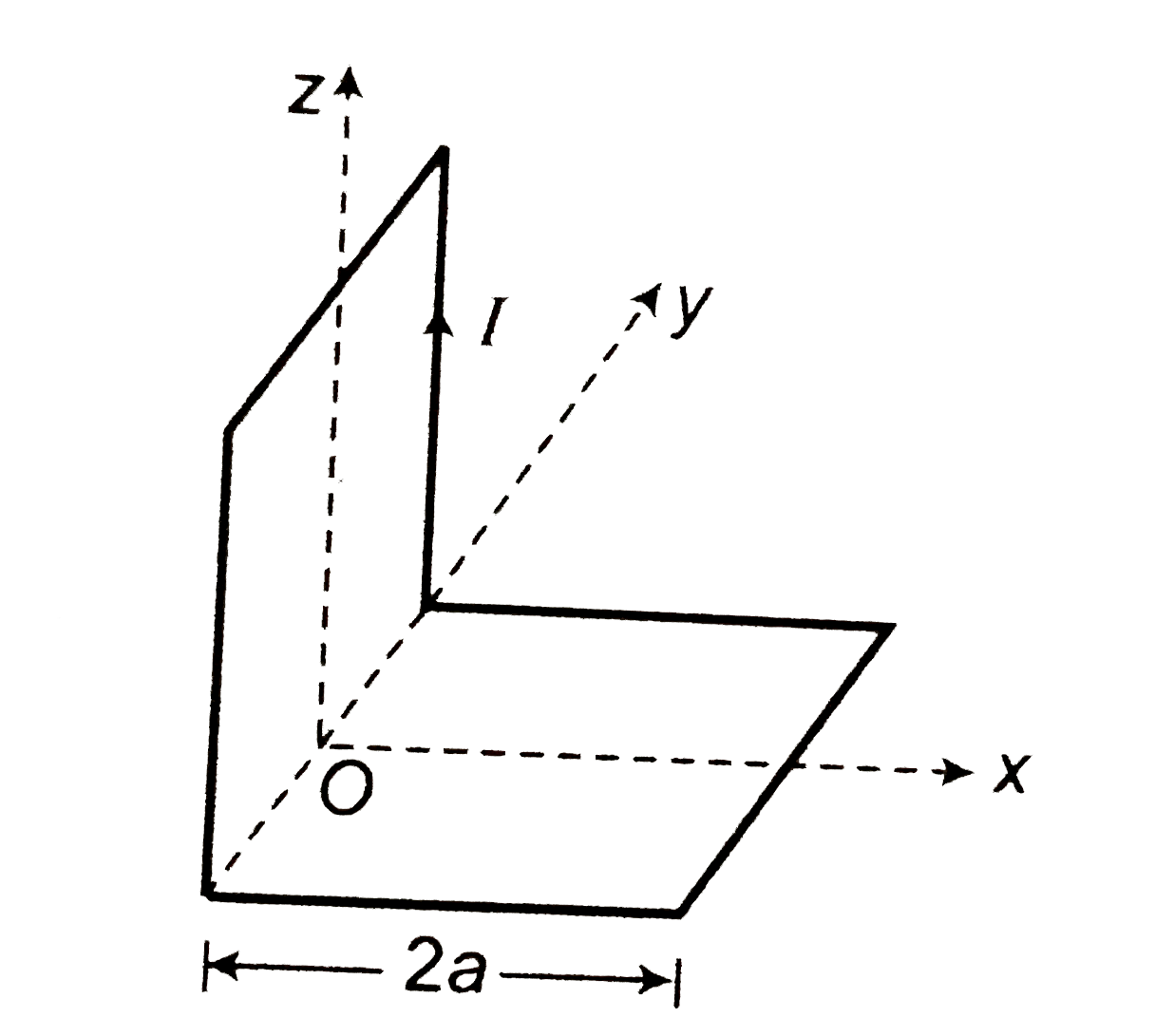
(c) A non-coplaner loop of conducting wire carrying a current I is placed as shown in the figure. Each of the straight sections of the loop of length 2a. find unit vector along magnetic field magnetic filed at the point P(a,0,a).
View SolutionA current carrying circular loop of radius R is placed in a uniform magnetic field B0 Tesla in x-y plane as shown in figure. The loop carries a current i=1A in the direction shown. Find the torqure acting on the loop
View SolutionA long straight wire along the z-axis carries a current I in the negative z-direction. The magnetic vector field →B at a point having coordinnates (x, y) in the z = 0 plane is
View SolutionA long straight wire along the z-axis carries a current I in the negative z-direction. The magnetic vector field B at a point having coordinate (x,y) on the z=0 plane is:
View Solution
