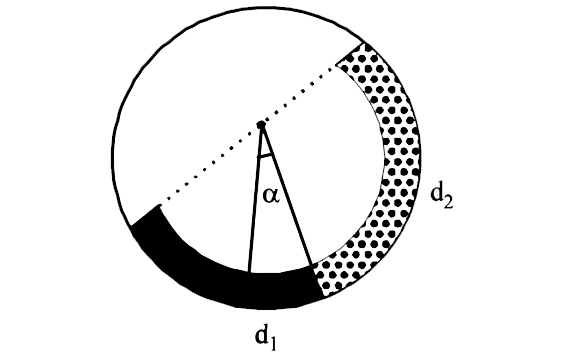
There is a circular tube in a vertical plane. Two liquids which do not mix and of densities are filled in the tube. Each liquid subtends angle at centre. Radius joining their interface make an angle with vertical. Ratio is :
The correct Answer is:A
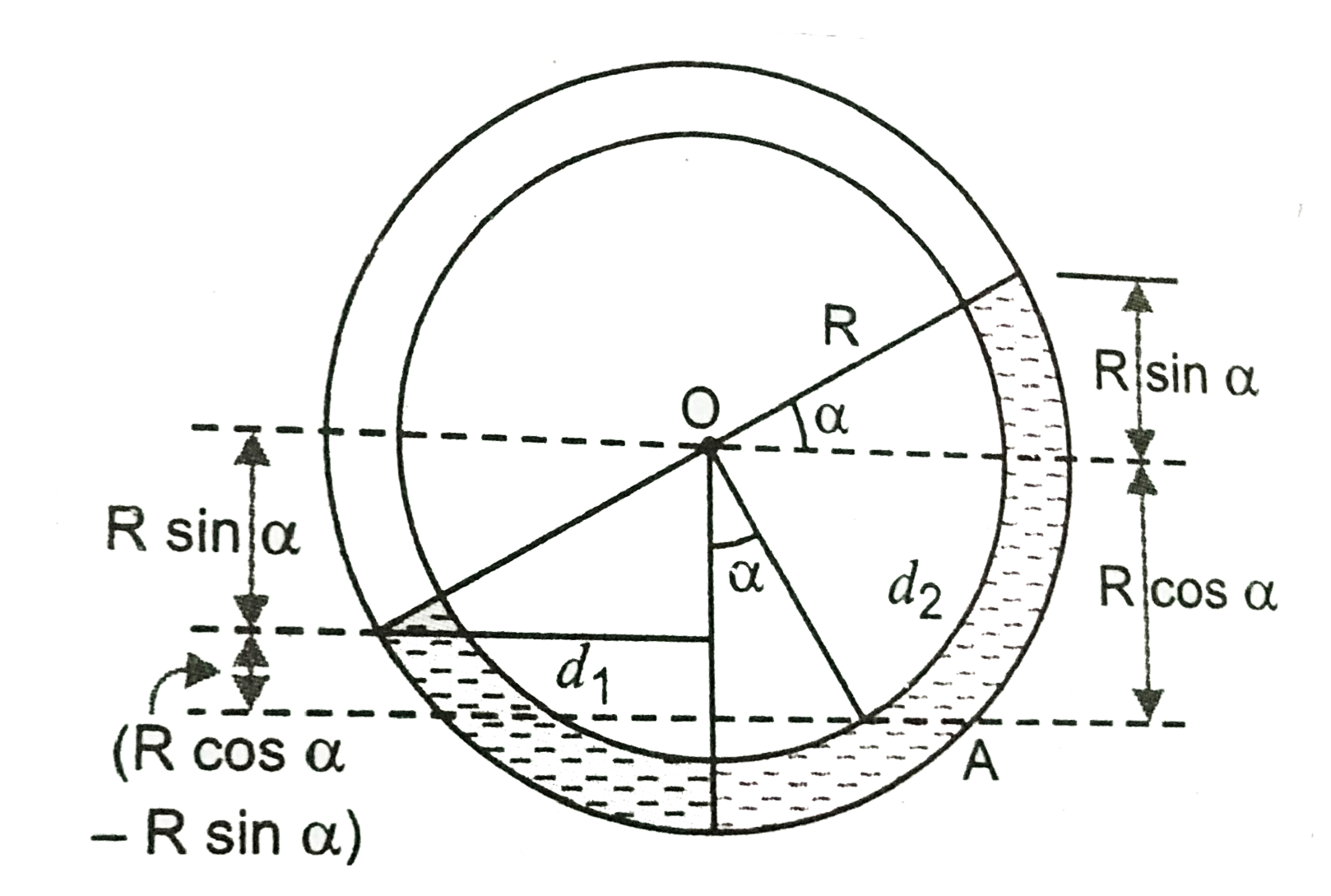
the pressure at A due to liquid of density
Pressure at A due to liquid of density
Let, = Pressure due to air in tube. Equating pressure at A, we get
or
Topper's Solved these Questions
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Integer Type Questions
12 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Asseration - Reason Type Question
18 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Multiple choice questions-II
14 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance
18 Videos
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)
25 Videos
Similar Questions
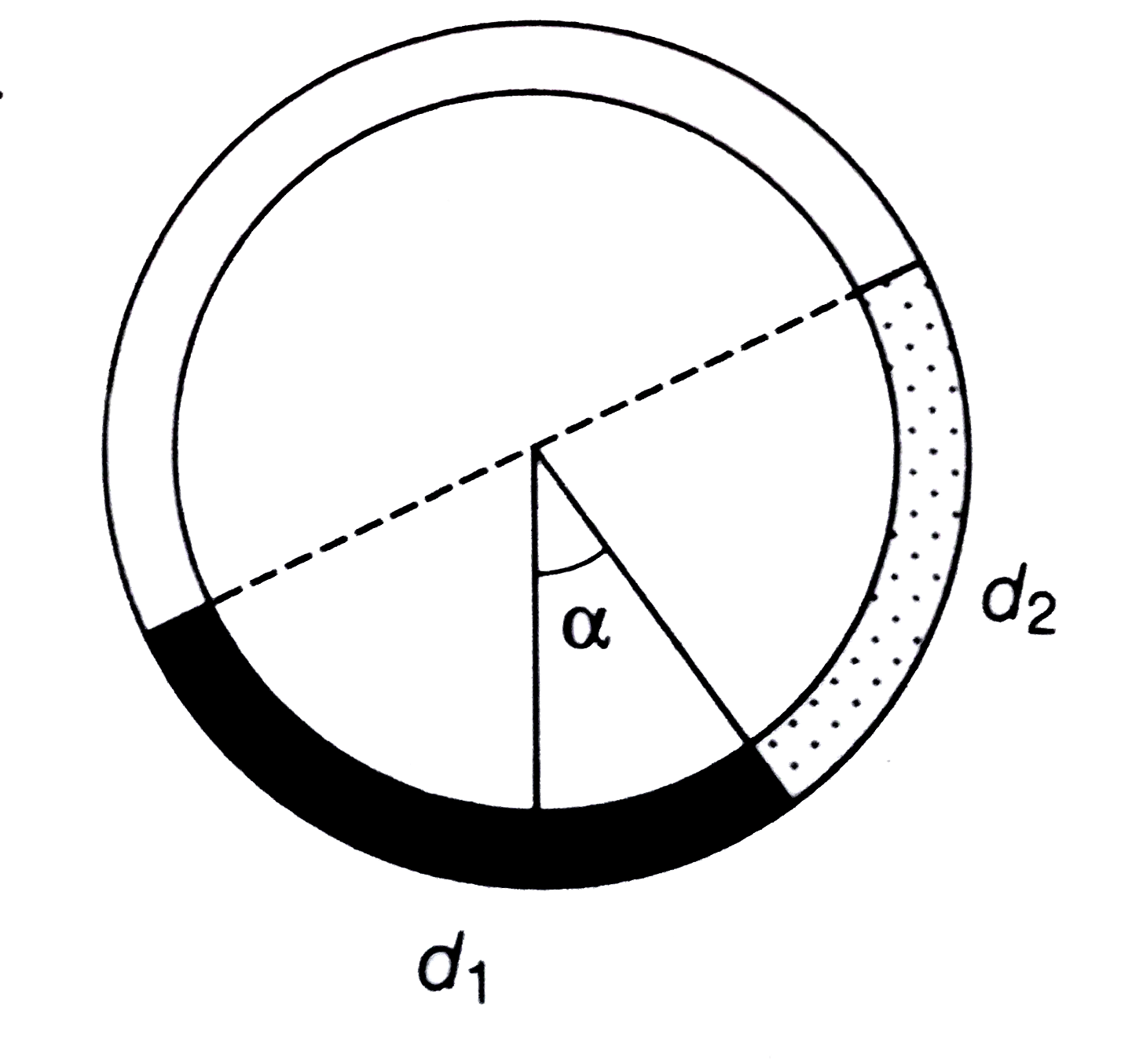
There is a circular tube in a vertical plane. Two liquids which do not mix and of densiities d1andd2 are filled I the tube. Each liquid subtends 90∘ angle at centre. Radius joining their interface makes an angle α with vertical. Ratio d1/d2 is
View SolutionA circular tube of uniform cross section is filled with two liquids densities ρ1 and ρ2 such that half of each liquid occupies a quarter to volume of the tube. If the line joining the free surfaces of the liquid makes an angle θ with horizontal find the value of θ.

View Solution
Knowledge Check
A thin uniform circular tube is kept in a vertical plane. Equal volume of two immiscible liquids whose densites are ρ1 and ρ2 fill half of the tube as shown. In equilibrium the radius passing through the interface makes an angle of 30∘ with vertical. The ratio of densities (ρ1/ρ2) is equal to
 A√3−12−√3B√3+12+√3C√3−1√3+1D√3+1√3−1
A√3−12−√3B√3+12+√3C√3−1√3+1D√3+1√3−1A uniform long tube is bent into a circle of radius R and it lies in vertical plane. Two liquids of same volume but densities ρ and δ fill half the tube. The angle θ is
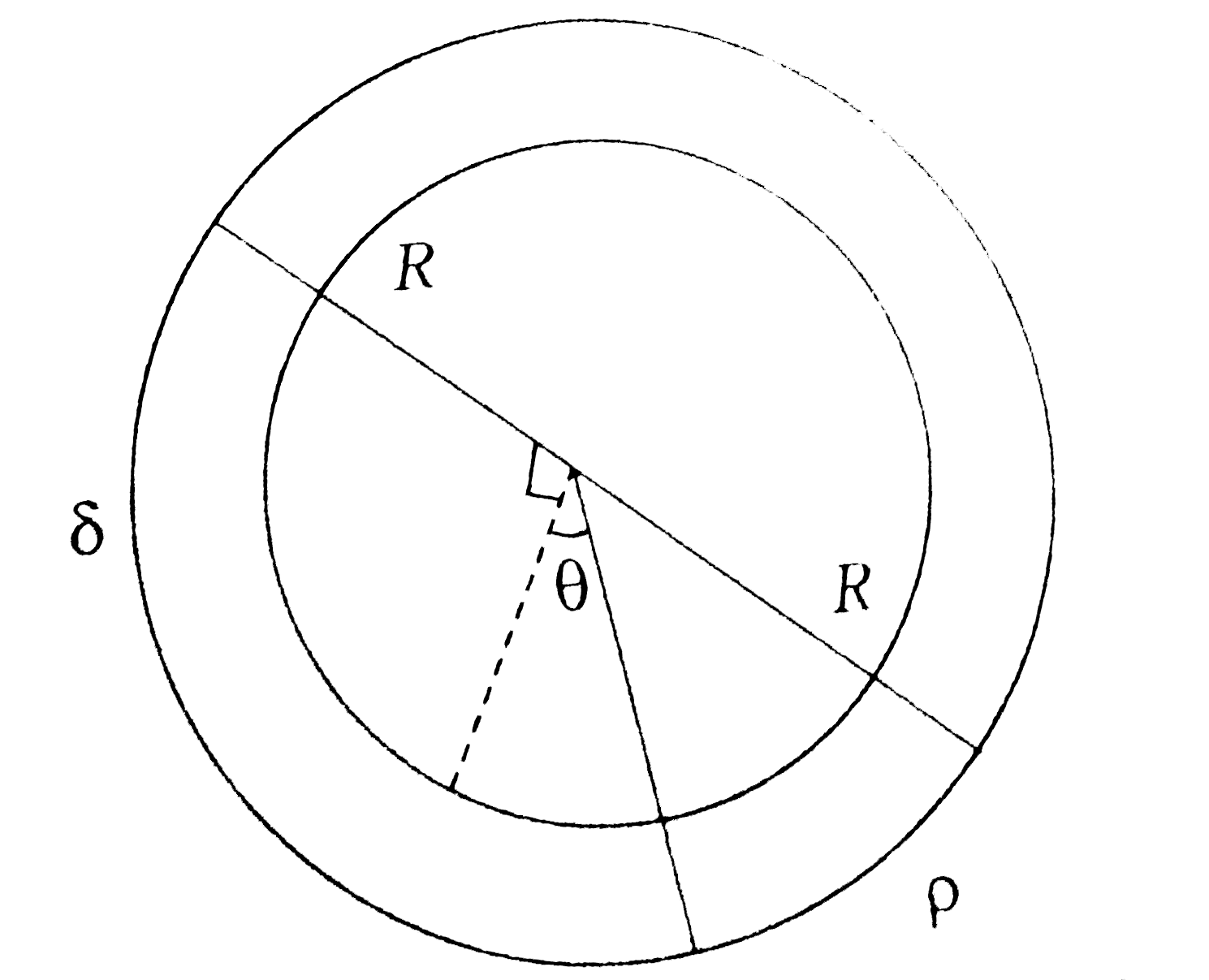 Atan−1(ρ−δρ+δ)Btan−1(ρδ)Ctan−1(δρ)Dtan−1(ρ+δρ−δ)
Atan−1(ρ−δρ+δ)Btan−1(ρδ)Ctan−1(δρ)Dtan−1(ρ+δρ−δ)If equal masses of two liquids of densities d1andd2 are mixed together, the density of the mixture is
Ad1d2(d1+d2)B2d1d2(d1+d2)Cd1d22(d1+d2)D(d1+d2)2
Two non-viscous, incompressible and immiscible liquids of densities p and 1.5p are poured into the two limbs of a circular tube of radius R and small cross section kept fixed in a vertical plane as shown in the figure. Each liquid occupies one fourth the circumference of the tube.
(i)Find the angle theta that the radius to the interface makes with the vertical in equilibrium position. _________
(ii) If the whole liquid column is given a small displacement from its equilibrium position, show that the resulting oscillations are simple harmonic. Find the time period of these oscillations. ____________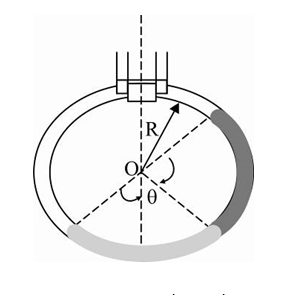
View SolutionA thin uniform tube is bent into a circle of radius r in the vertical plane. Equal volumes of two immiscible liquids, whose densities are ρ1 and ρ2(ρ1>ρ2) fill half the circle. The angle θ between the radius vector passing though the common interface and the vertical is :
View SolutionThree liquids of densities d,2d , and 3d are mixed in equal volumes. Then the density of the mixture is
View SolutionA small uniform tube is bent into a circle of radius r whose plane is vertical. Equal volumes of two fluids whose densities areρ and σ(ρ>σ) fill half the circle. Find the angle that the radius passing through the interface makes with the vertical.
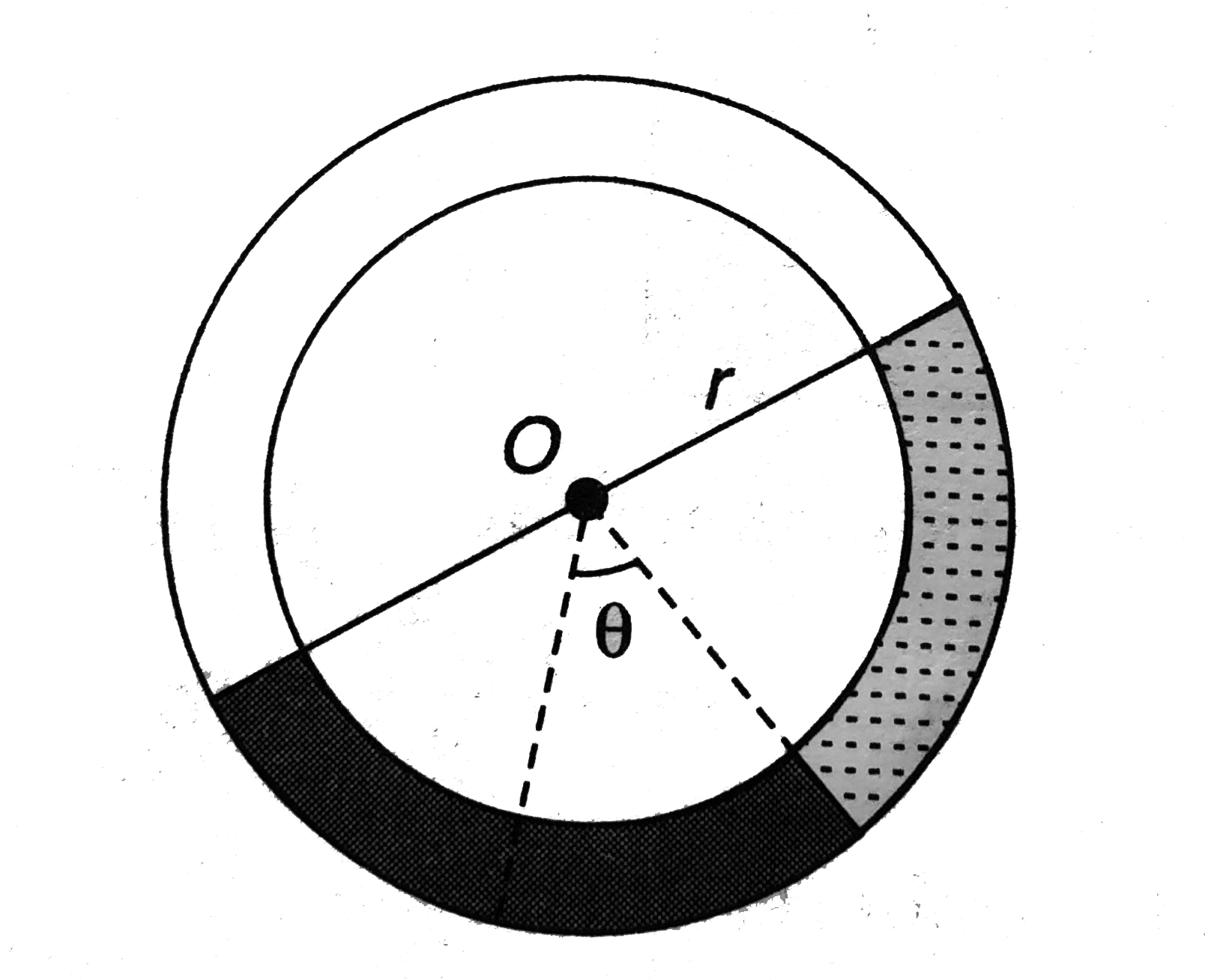
View SolutionWhen a body of density d1 and volume V is floating in a liquid of density d2
View Solution
