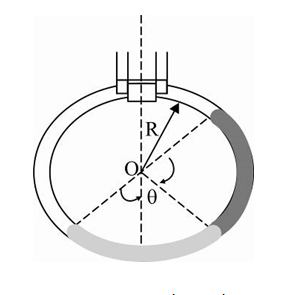
Two non-viscous, incompressible and immiscible liquids of densities p and 1.5p are poured into the two limbs of a circular tube of radius R and small cross section kept fixed in a vertical plane as shown in the figure. Each liquid occupies one fourth the circumference of the tube.
(i)Find the angle theta that the radius to the interface makes with the vertical in equilibrium position. _________
(ii) If the whole liquid column is given a small displacement from its equilibrium position, show that the resulting oscillations are simple harmonic. Find the time period of these oscillations. ____________
The correct Answer is:tan−1(15), (ii)2.5√R
(i) tan−1(15) (ii) 2.5√R
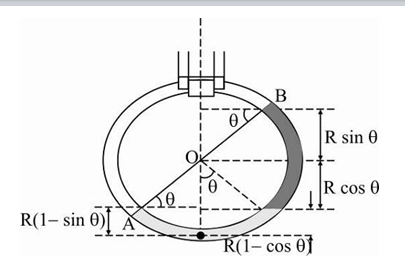
(i) The pressure due to liquid on left limb (at bottom)
P1=R(1sinθ)1.5pg ...(i)
The pressure due to liquids on right limb
P2=(Rsinθ+Rcosθ)pg+R(1−cosθ)1.5pg ...(ii)
In equilibrium, P1=P2
Which gives, tanθ=(15)⇒θ=tan−1(15)
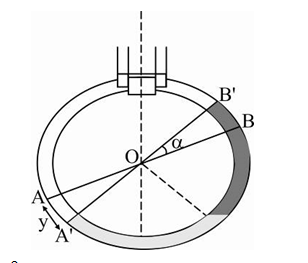
(ii) If the liquid is given a small angular displacement α, the pressure difference, dP=P1−P2 dP=[Rsinθ+α)+Rcos(θ+α)]pg+R[l−cos(θ+α)]1.5pg−R[l−sin(θ+α)]1.5pg
As α is small, sinα=α,cosα=1
dP=Rpg[2.5sinθ+2.5cosθα−0.5cosθ+0.5sinθα]
tanθ=0.2,sinθ=0.2√1.04 and cosθ=1√1.04
dP=2.55Rpgα=2.55pgy(as Ra=y)
Restoring force F=dPx area =−2.55pgA
Mass of the liquid in tube m=2πR4Ap+2πr4A×1.5p=1.25πRAp
Hence acceleration a=Fm=−2.55pgyA1.25πRAp,a=−2.04(gπR)y, a=−ω2y
Hence, ω=√2.04(gπR), Time period, T=2πω=2.5√Rsec
Similar Questions
Two non - viscous, incompressible and immiscible liquids of densities (rho) and (1.5 rho) are poured into the two limbs of a circular tube of radius ( R) and small cross section kept fixed in a vertical plane as shown in fig. Each liquid occupies one fourth the cirumference of the tube.
Find the angle (theta) that the radius to the interface makes with the verticles in equilibrium position.
View SolutionTwo non-viscous, incomoressible and immiscible liquids of densities ρ and 1.5ρ are poured into the two limbs of a circules tube of radius R and small cross-section kept fixed in a vertical plane as shown in fig. Each liquid occupies one-fourth the cirumference of the tube.

(a) Find the angle θ the radius to the interface makes with the vertical in equilibrium position.
(b) If the whole liquid column is given a small displacement from its equilibrium position, show that the resulting oscillations alre simple harmonic. Find the time period of these oscillations.
View Solution
Knowledge Check
A small uniform tube is bent into a circle of radius r whose plane is vertical. Equal volumes of two fluids whose densities areρ and σ(ρ>σ) fill half the circle. Find the angle that the radius passing through the interface makes with the vertical.
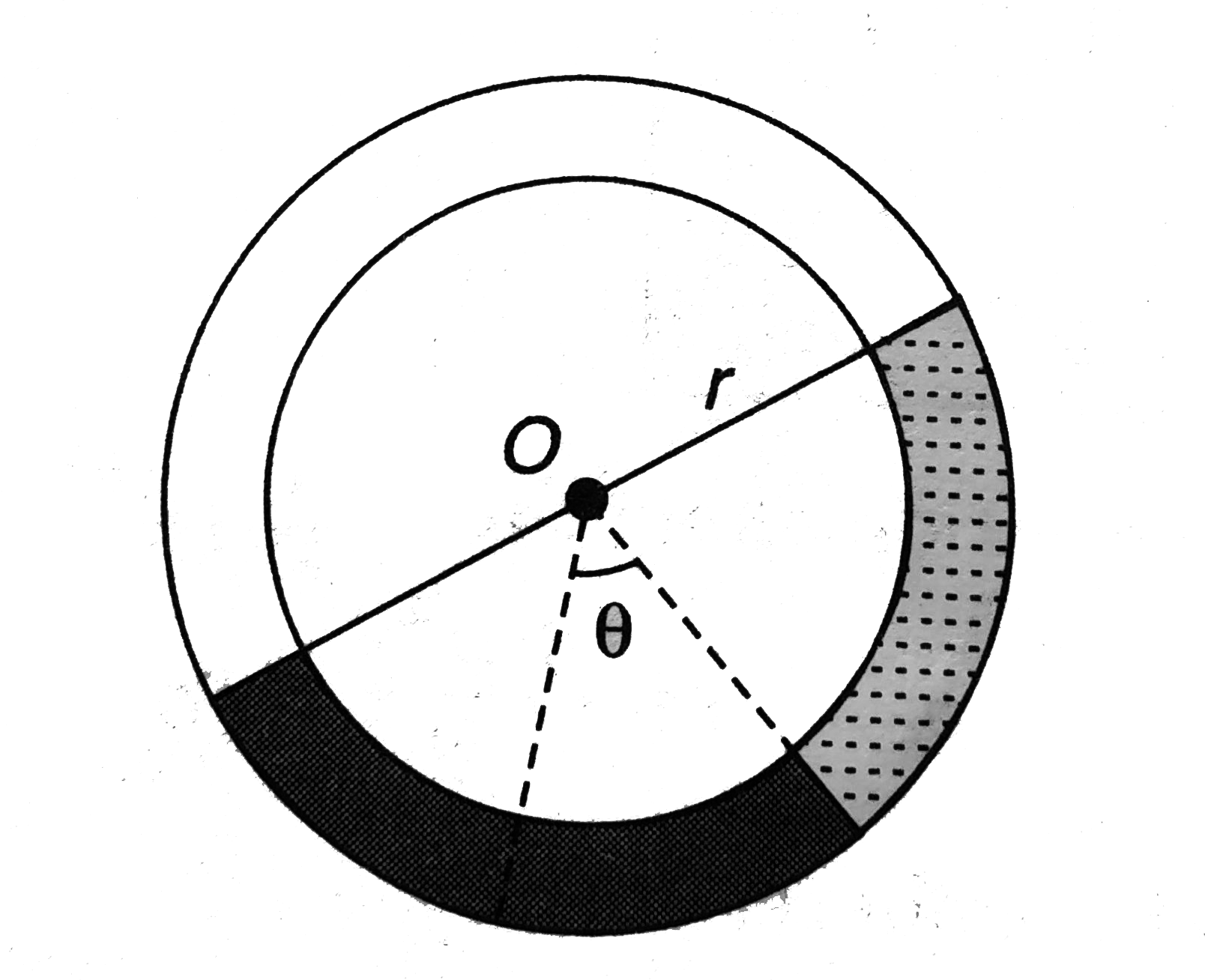 Atan−1(ρ+σρ−σ)Btan−1(ρ−σρ−σ)Ctan−1(ρ+σρ+σ)Dtan−1(ρ−σρ+σ)
Atan−1(ρ+σρ−σ)Btan−1(ρ−σρ−σ)Ctan−1(ρ+σρ+σ)Dtan−1(ρ−σρ+σ)A V-shaped glass tube of uniform cross section is kept in a vertical plane as shown. A liquid is poured in the tube. In equilibrium the level of liquid in both limbs of tube are equal. Find the angular frequency of small oscillation of liquid.
 Aπ√2hgsinα.sinβB2π√hgsinα.sinβC2π√h2gsinα.sinβDNone of these
Aπ√2hgsinα.sinβB2π√hgsinα.sinβC2π√h2gsinα.sinβDNone of theseA thin uniform tube is bent into a circle of radius r in the vertical plane. Equal volumes of two immiscible liquids, whose densities are ρ1 and ρ2(ρ1>ρ2) fill half the circle. The angle θ between the radius vector passing though the common interface and the vertical is :
Aθ=tan−1'π2(ρ2ρ1)Bθ=tan−1'π(ρ1ρ2)Cθ=tan−1'π2(ρ1+ρ2ρ1−ρ2)Dθ=tan−1'[π2(ρ1+ρ2ρ1−ρ2)]
A small uniform tube is bent into a circle of radius r whose plane is vertical. Equal volumes of two fluids whose densities areρ and σ(ρ>σ) fill half the circle. Find the angle that the radius passing through the interface makes with the vertical.

View SolutionA V-shaped glass tube of uniform cross section is kept in a vertical plane as shown. A liquid is poured in the tube. In equilibrum the level of liquid in both limds of tube. Find the angular frequency of small oscillation of liquid.

View SolutionA circular tube of uniform cross section is filled with two liquids densities ρ1 and ρ2 such that half of each liquid occupies a quarter to volume of the tube. If the line joining the free surfaces of the liquid makes an angle θ with horizontal find the value of θ.

View SolutionA circular tube of uniform cross section is filled with two liquids densities ρ1 and ρ2 such that half of each liquid occupies a quarter to volume of the tube. If the line joining the free surfaces of the liquid makes an angle θ with horizontal find the value of θ.

View SolutionThere is a circular tube in a vertical plane. Two liquids which do not mix and of densities d1andd2 are filled in the tube. Each liquid subtends 90∘ angle at centre. Radius joining their interface make an angle α with vertical. Ratio d1d2 is :
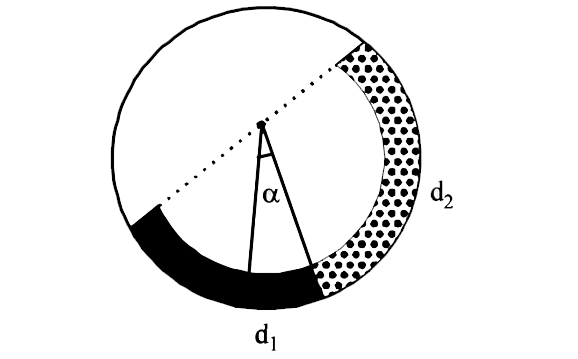
View Solution
