There is a narrow beam of negative pions with kinetic energy T equal to the rest energy of these particles. Find the ratio of fluxes at the sections of the beam separated by a distance l=20m. The proper mean lifetime of these poins is τ0=25.5ns.
Here η=Tmc2=1 so the life time of the pion in the laboratory frame is
η=(1+η)τ0=2τ0
The law of radioactive decay implies that the flux decrease by the factor.
JJ0=e−t/τ=e−l/vt=e−l/cτ0√η(2+η)
=exp(−mclτ0√T(T+2mc2))=0.221
Topper's Solved these Questions
Similar Questions
Negative points with kinetic energy T=100MeV travel an average distance l=11m from origin to decay. Find the proper lifetime of these poins.
View SolutionFind the mean path travelled by pions whose kinetic energy exceeds their rest energy η=1.2times. The mean lifetime of very slow pions is τ0=25.5ns.
View SolutionA particles of rest mass m0 with kinetic energy T strikes a stationary particle of the same rest mass. Find the rest mass and the velocity of the compound particle formed as a result of the collision.
View SolutionA narrow beam of alpha particles with kinetic energy T=0.50MeV and intensity I=5.0.105 particles per second falls normally on a golden foil. Find the thickness of the if at a distance r=15cm from a scattering section of that foil the flux density of scatteered particles at the angle θ=60∘ to the incident beam is equal to J=40 particles/(cm2.s).
View SolutionA stationary neutral particle disintegrated into a proton with kinetic energy T=5.3MeV and a negative pion. Find the mass of that particle. What is its name.
View SolutionFind the ratio of kinetic energy of the particle to the energy of the photon . If the de Broglie wavelength of a particle moving with a velocity 2.25×108m/s is equal to the wavelength of photon .
View SolutionA narrow beam of alpha particles with kinetic energy T=600keV falls normally on a golden foil incorporating n=1.1.1019 nuclei/cm2. Find the fraction of alpha particles scattered thtough the angles θ<θ0=20∘
View SolutionFind the ratio of kinetic energy of the particle to the energy of the photon . If the de Broglie wavelength of a perticle moving with a volecity 2.25×108m/s is equal to the wavelength of photon .
View SolutionA thin beam of charged particles in incident normally on the boundry of a region containing a uniform magnetic field as shown.The beam comprise of mono energetic α and β(−) particles, each possessing a kinetic energy T.Neglecting interaction between particles of the beam, find the separation between the points on line PQ where the α and β particles emerge out of the magnetic field.(express your answer in terms of T,B,α(2e,mα)&β−(−e,me),where all terms have their usual meanings.)
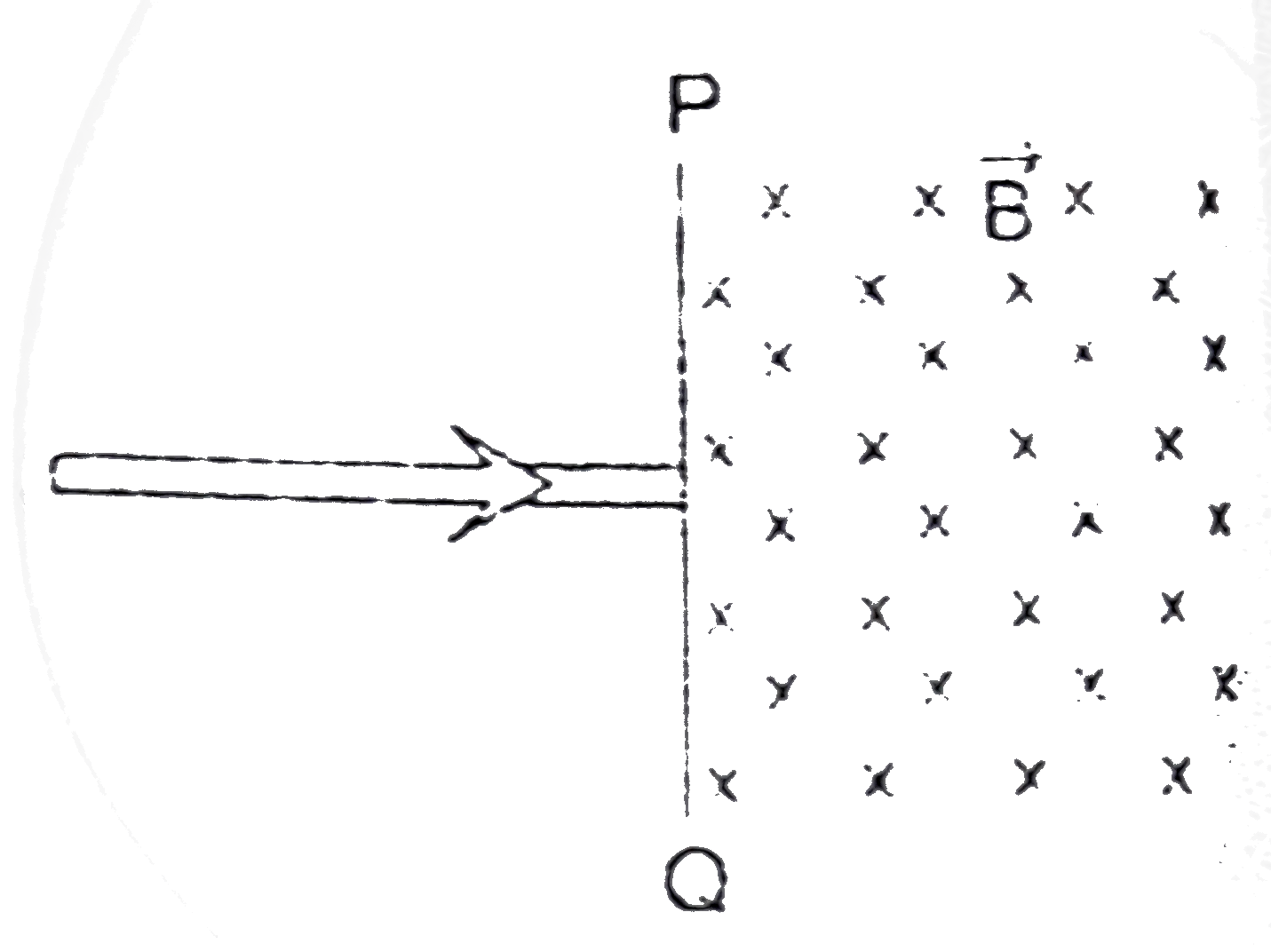
View SolutionA thin beam of charged particles in incident normally on the boundry of a region containing a uniform magnetic field as shown.The beam comprise of mono energetic α and β(−) particles, each possessing a kinetic energy T.Neglecting interaction between particles of the beam, find the separation between the points on line PQ where the α and β particles emerge out of the magnetic field.(express your answer in terms of T,B,α(2e,mα)&β−(−e,me),where all terms have their usual meanings.)

View Solution
