Find the kinetic energy of a neutron emerging as a result of the decay of a stationary Σ−hyperon(Σ−→n+π−).
We have O=−→pn+→pπ....(1)
mΣc2=En+Eπ
or (mΣc2−En)2=E2π
or m2Σc4−2mΣc2En=E2π−E2n=c4m2π−c4m2n
because (1) implies E2π−E2n=m2πc4−m2n−m2nc4
Hence En=m2Σ+m2n−m2π2mΣc2
and Tn=(m2Σ+m2n−m2π2mΣ−mn)c2=(MΣ−mn)2−m2π2mΣc2
Substitution gives Tn=19.55MeV
Topper's Solved these Questions
Similar Questions
Find the number of σ bond and π bonds present in Marshall's acid?
View SolutionA moving neutron collides with stationary H-atom in ground state. As a result it excites and then de-excites. The corresponding radiation fail on a surface having work function σ. The minimum value of required kinetic energy for neutron is E0 and possible minimum value of de-Broglie wavelength of emitted photoelectrons is λ0. If the neutron hits stationary (He)+ ion instead of stationary (H) atom, then the minimum value of kinetic energy for neutron is E1 and the value of energy. transferred from neutron to H-atom is xE0y. Find (xy).
View Solution
Knowledge Check
The number of 'sigma' and π electrons in methanol are
A6 and 2B2 and 6C4 and 4D4 and 2Find the number of σ and π bonds present in Vinyl benzoate
A21 and 6B22 and 6C19 and 6D19 and 5
A neutron collides elastically with an initially stationary deuteron. Find the fraction of the kinetic energy lost by the neutron
(a)in a head-on collision
(b) in scatterting at right angles.
View SolutionA neutron collides elastically with an initially stationary deuteron. Find the fraction of the kinetic energy lost by the neutron (a) in a head-on collision , (b) in scattering at right angles.
View SolutionFind the kinetic energy that must be imparted to a positron for a proton-antiproton pair to be obtained as a result of its collision with a stationary electron.
View SolutionA neutron at rest decays. Assuming the resulting proton to remain at rest, too, find the kinetic energy of the electron and the energy of the antineutrino.
View SolutionA neutron at rest decays. Assuming the resulting proton to remain at rest, too, find the kinetic energy of the electron and the energy of the antineutrino.
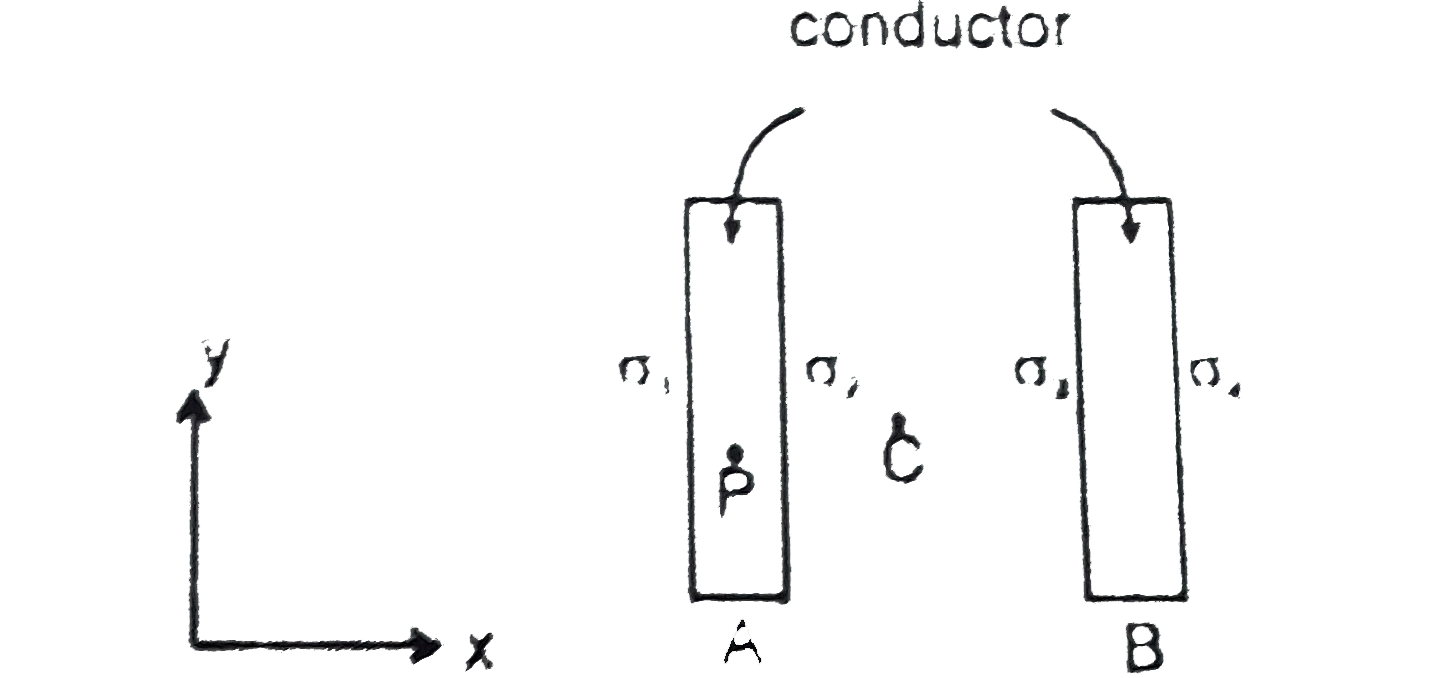
View SolutionFigure shown two infinitely large conducting plates A and B. If electric field at C due to charge densities σ1,σ2,σ3 and σ40 is Eˆi, find σ2 and σ3 in terms of E. Derive a relation between σ1 and σ4.
View Solution
