Three capacitors of capacitances 5μF,4μFand7μF are connected in different possible combinations. Calculate the minimum and maximum effective capacitance possible from all possible combinations.
To solve the problem of finding the minimum and maximum effective capacitance from the given capacitors of capacitances 5μF, 4μF, and 7μF, we will follow these steps:
Step 1: Understanding the Configuration
- Capacitors can be connected in two main configurations: series and parallel.
- In series, the total capacitance decreases, while in parallel, it increases.
Step 2: Calculate Minimum Effective Capacitance (Series Connection)
1. Formula for Series Connection:
1Ceq=1C1+1C2+1C3
where C1=5μF, C2=4μF, and C3=7μF.
2. Substituting the Values:
1Ceq=15+14+17
3. Finding a Common Denominator:
- The least common multiple (LCM) of 5, 4, and 7 is 140.
4. Calculating Each Term:
15=28140,14=35140,17=20140
5. Adding the Terms:
1Ceq=28+35+20140=83140
6. Finding Ceq:
Ceq=14083≈1.68μF
Step 3: Calculate Maximum Effective Capacitance (Parallel Connection)
1. Formula for Parallel Connection:
Ceq=C1+C2+C3
2. Substituting the Values:
Ceq=5μF+4μF+7μF
3. Calculating the Total:
Ceq=5+4+7=16μF
Conclusion
- The minimum effective capacitance when connected in series is approximately 1.68μF.
- The maximum effective capacitance when connected in parallel is 16μF.
- Capacitors can be connected in two main configurations: series and parallel.
- In series, the total capacitance decreases, while in parallel, it increases.
1. Formula for Series Connection:
1Ceq=1C1+1C2+1C3
where C1=5μF, C2=4μF, and C3=7μF.
1Ceq=15+14+17
- The least common multiple (LCM) of 5, 4, and 7 is 140.
15=28140,14=35140,17=20140
1Ceq=28+35+20140=83140
Ceq=14083≈1.68μF
1. Formula for Parallel Connection:
Ceq=C1+C2+C3
Ceq=5μF+4μF+7μF
Ceq=5+4+7=16μF
- The minimum effective capacitance when connected in series is approximately 1.68μF.
- The maximum effective capacitance when connected in parallel is 16μF.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Conceptual Questions
37 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Tough & Tricky PROBLEMS
10 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - PRACTICE PROBLEMS 4
7 Videos
- ELECTROMAGNETIC WAVESBOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST
14 Videos
- MAGNETISM AND MATTERBOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
16 Videos
Similar Questions
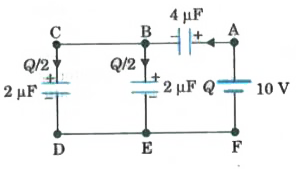
Three capacitors of capacitances 2μF,2μFand4μF are connected to a battery of 10V as shown in the figure. Calculate the effective capacitance of the circuit and charge on each capacitor.
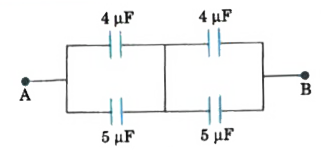
View SolutionTwo capacitors of capacitances 4μF and another two of 5μF are connected as shown in the given figure (f). Calculate the effective capacitance across points A and B.
View Solution
Knowledge Check
Three capacitors of capacitances 1μF,2μFand4μF are connected first in a series combination, and then in parallel combination. The ratio of their equivalent capacitances will be
A2:49B49:2C4:49D49:4Three capacitors of capacitance 3μF,10μF and 15μF are connected in series to a voltage source of 100V. The charge on 15μF is
A50μCB100μCC200μCD280μCThree capacitors of capacitances 3μF,9μF and 18μF are connected one in series and another time in parallel. The ratio of equivalent capacitance in the two cases (CsCp) will be
A1:15B15:1C1:1D1:3
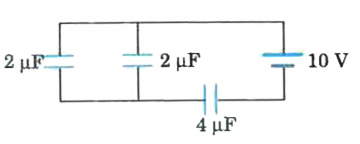
Three capacitors of capacitances 2μF,2μFand4μF are connected across a battery of 10V as shown in the adjoining figure (g). Calculate the effective capacitance and charge on each capacitor.
View SolutionThree capacitances of capacity ,10 muF, 5 muF" and "5muF" are connected in parallel.The total capacity will be
View SolutionThree capacitors of capacities 8μF,8μFand4μF are connected in a series and a potential difference of 120 volt is maintained across the combination. Calculate the charge on capacitor of capacity 4μF.
View SolutionThree capacitors of capacitance 3μF are connected in a circuit. Then their maximum and minimum capacitances will be
View SolutionThree capacitors of capacitance 3μF are connected in a circuit. Then, their maximum and minimum capacitance will be
View Solution
