Three capcitors of capacitances 4μF,
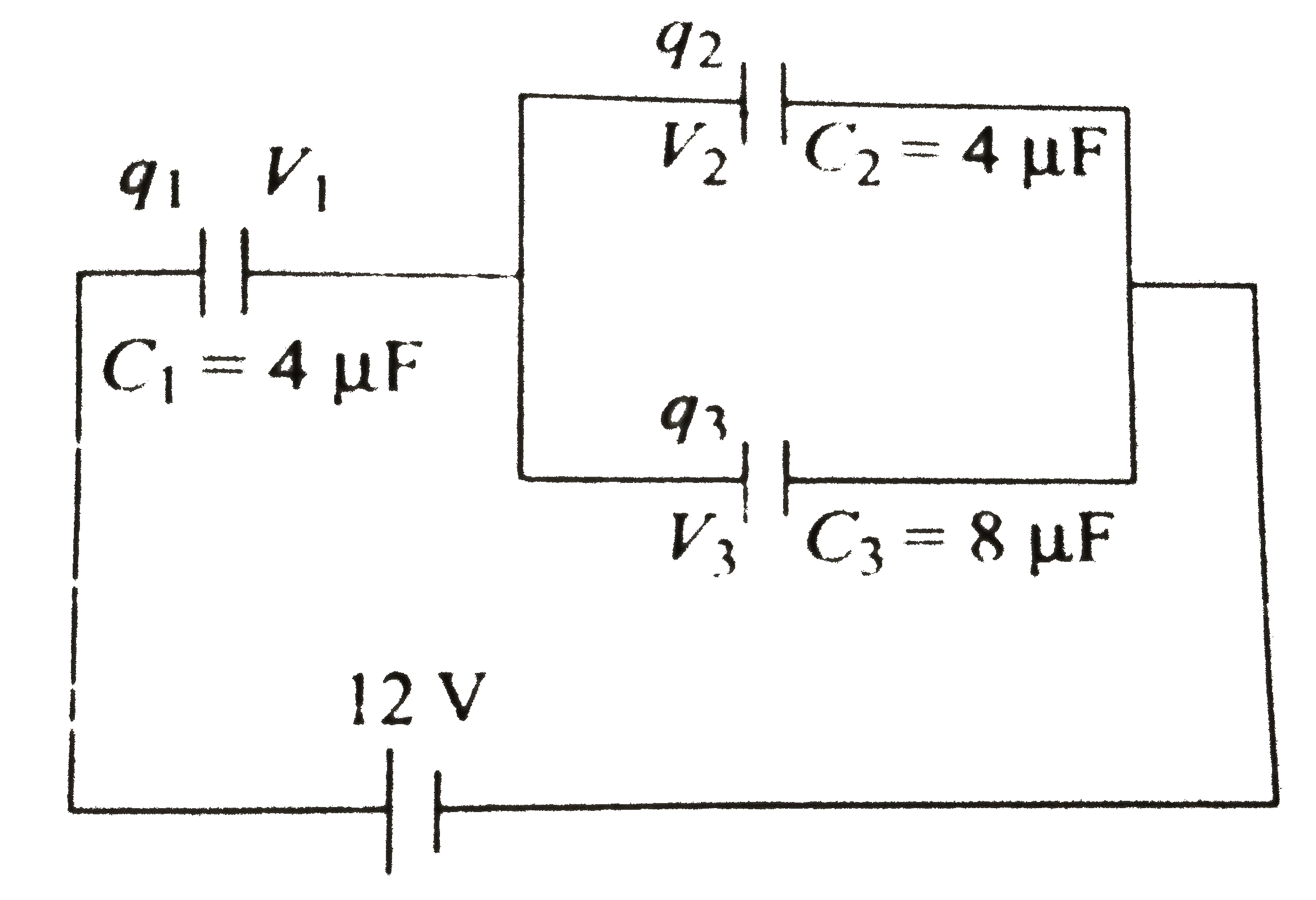 .
.
4μF, and 8μF, are connected as show across a battery of emf 12V.
i. Find the equivalent capacitane.
ii. Find the potential difference and charge on each capacitor.
iii. Find the energy stored in each capacitor and the total energy stored in the system of capacitors.
C2 and C3 are in parallel, so their equivalent capacitance is
C'=C2=4+8=12μF
This C' will be in series with C1, so the net equilvent capacitance is
Ceq=C1C'C1+C'=4×124+12=3μF
ii. q1=CeqV=3×12=36μC
q1 will be divded into q2 and q3, So
q2=C2q1C2+C3=4×364+=12μC
q3=C3q1C2+C3=8×364+8=24μC
V1=q1C1=364=9V
V2=V3=q2C2=Q3C3=364=3V

Alternatively, potentials can also be calculated by dividing 12V and the inverse ratio of C1 and C'
V1=C'VC1+C'=12×124+12=9V
V2=V3=C1VC1+C'=4×122+12=3V
(iii) Ui=12C1V21=12×4×92=162μJ
U2+12C2V22=12×4×33=18μJ
U3=12C3V23=12×8×33=36μJ
Total energy is U1+U2+U3=216μJ
Alternatively
U=12CeqV2=12×3×(12)2=216μJ .
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Solved Examples10videos
CAPACITOR AND CAPACITANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Exercise 4.113videos
CAPACITOR AND CAPACITANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - ddp.4.315videos
ATOMIC PHYSICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type51videos
CENGAGE PHYSICS DPP
Similar Questions
Three capacitors of capacitances 3μF, 6μF, and 4μF are connected as shown across a battery of emf 6V.
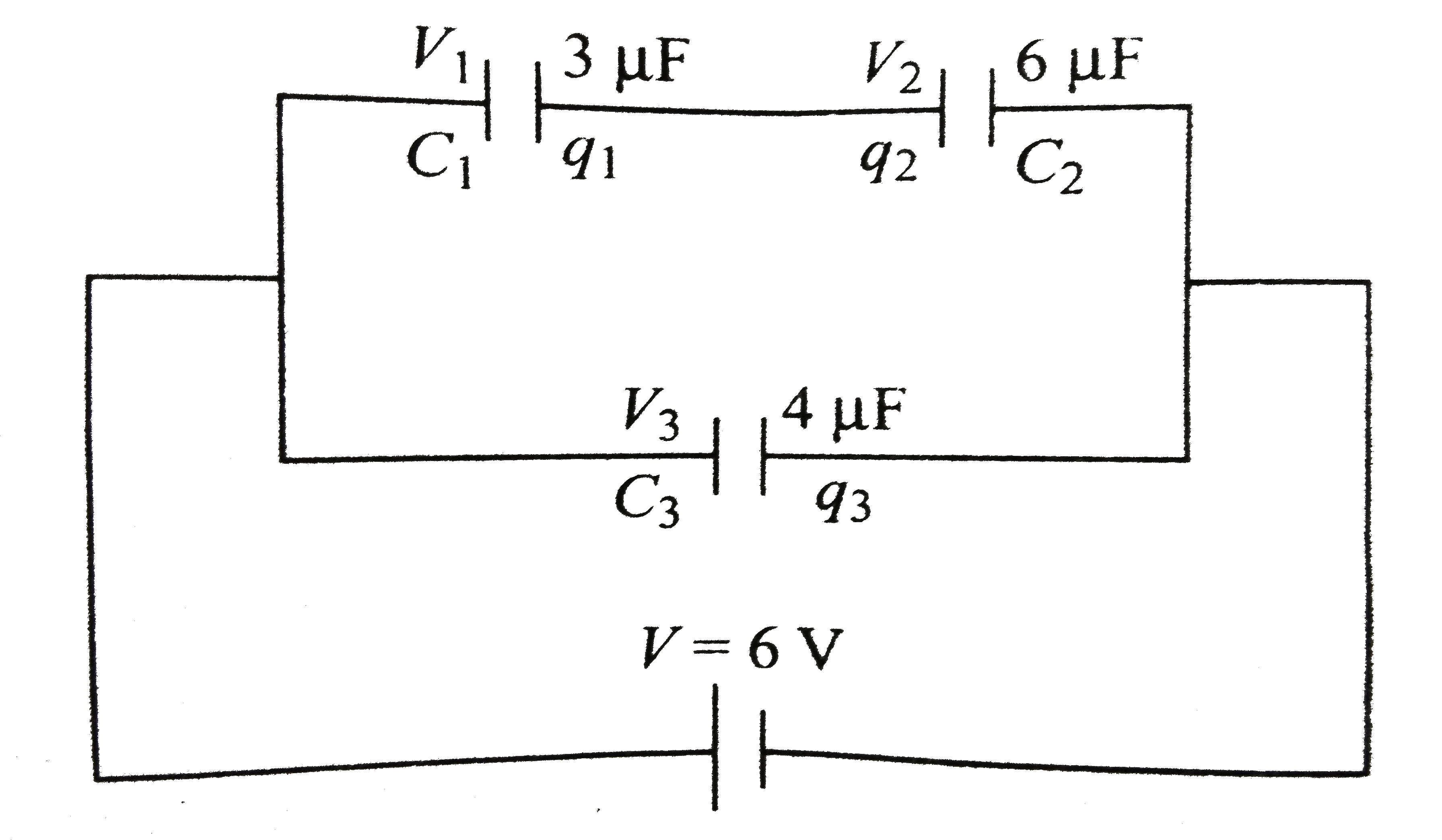 .
.
i. Find the equivalent capacitance,
ii. Find the potential difference and charge on each capacitor.
iii. Find the energy stored in the system of capacitors and total energy stored in the system of capacitor.View SolutionThe energy stored in 4μF capacitors is
View SolutionFind the potential difference and charge on each capacitance. All capacitances are in μF.
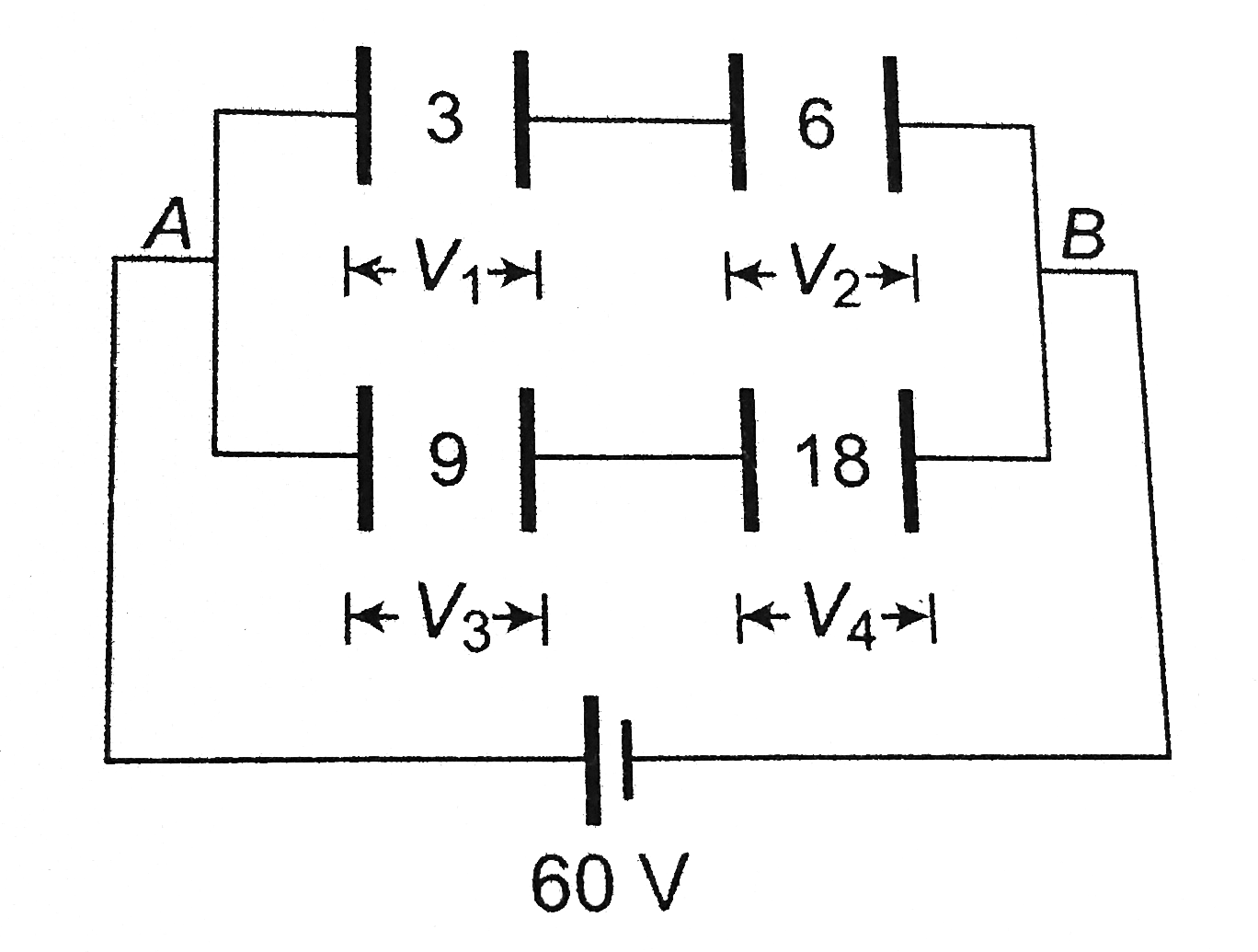 View Solution
View SolutionFind charge on each capacitor and potential difference across each capacitor .
 View Solution
View SolutionFind the equivalent capacitance between points A and B. Capacitance of each capacitor is 2μF.
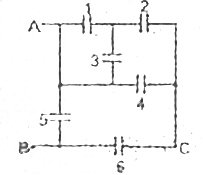 View Solution
View SolutionTwo capacitor of capacitance 4.0μFand 6.0muF' are connected in series with a battery of 20 V . Find the energy supplied by the battery .
View SolutionTwo capacitors of capacitances 20.0pF and 50.0pF are connected in series with a 6.00V bettery . Find (a )the potential difference across each capacitor and (b) the energy stored in each capacitor .
View SolutionIn the circuit shown in figure 3.141, find the energy stored in 4μF capacitor in steady state.
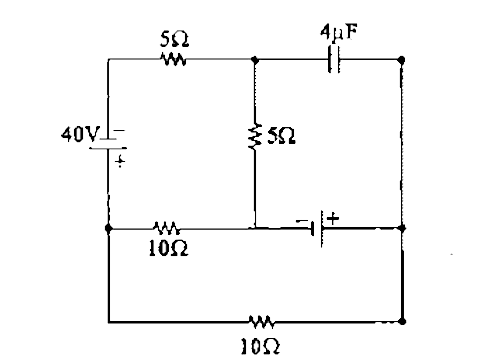 View Solution
View SolutionThree capacitors of capacitances 1μF,2μFand4μF are connected first in a series combination, and then in parallel combination. The ratio of their equivalent capacitances will be
View SolutionIn the adjoning figure, the potential difference across the 4.5μF capacitor is
 View Solution
View Solution


