Three charges are placed at the vertices of an equilateral triangle of side 'a' as shown in the following figure. The force experienced by the charge placed at the vertex. A in a direction normal to BC is
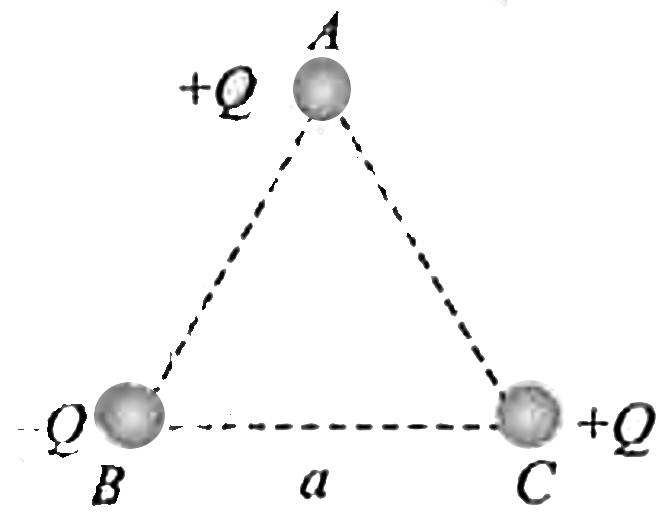
Q24π∈0a2
−Q24π∈0a2
zero
Q22π∈0a2
The correct Answer is:C
FR=2Fcosθ/2
=2Fcos120/2=2Fcos60
=F=kQ2a2=Q24πε0a2

However, this force is the resultant force parallel to BC.
∴ Force perpendicular to BC is zero.
Similar Questions
Knowledge Check
Three masses each of mass m are palced at the vertices of an equilateral triangles ABC of side l as shown in figure. The force acting on a mass 2m placed at the centroid O of the triangle is
 AzeroB3Gm2l2C5Gm2l2D7Gm2l2
AzeroB3Gm2l2C5Gm2l2D7Gm2l2Consider the charges q,q and -q placed at the vertices of an equilateral triangle of each side l. What is the force on each charge ?
Aq24√2πε0l2B−q24πε0l2Cq24πε0l2Dzero
Three charges Q,(+q) and (+q) are placed at the vertices of an equilateral triangle of side l as shown in the figure. It the net electrostatic energy of the system is zero, then Q is equal to

View SolutionThree charges Q,(+q) and (+q) are placed at the vertices of an equilateral triangle of side l as shown in the figure. It the net electrostatic energy of the system is zero, then Q is equal to

View SolutionThree charges 2q,−q,and−q are located at the vertices of an equilateral triangle. At the center of the triangle,
View SolutionThree point charges q are placed at three vertices of an equilateral triangle of side a. Find magnitude of electric force on any charge due to the other two.
View Solution(a) Three point charges q,-4q and 2q are placed at the vertices of an equilateral triangle ABC of side 'l' as shown in the figure. Obtain the expression for the magnitude of the resultant electric force acting on the charge q.
(b) Find out the amount of the work 4one to separate the charges at infinite distance.

View SolutionFive point charges each of charge +q are placed on five vertices of a regular hexagon of side h as shown in the figure. Then
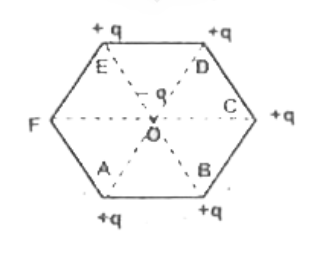
View Solution

