Find the coordinates of the vertices of an equilateral triangle of side 2a as shown in Figure.
To find the coordinates of the vertices of an equilateral triangle with a side length of 2a, we can follow these steps:
Step 1: Understand the Position of the Triangle
We will place one vertex of the triangle at the origin, O(0,0). The other two vertices will be positioned based on the properties of an equilateral triangle.
Step 2: Determine the Coordinates of Vertex A
Since one side of the triangle is horizontal, we can place vertex A at a distance of 2a along the x-axis from the origin. Therefore, the coordinates of vertex A will be:
A(2a,0)
Step 3: Calculate the Height of the Triangle
The height h of an equilateral triangle can be calculated using the formula:
h=√32×side
For our triangle, the side length is 2a:
h=√32×2a=√3a
Step 4: Determine the Coordinates of Vertex B
Vertex B will be positioned directly above the midpoint of the base OA. The midpoint of OA can be calculated as:
Midpoint=(0+2a2,0+02)=(a,0)
Now, we can find the coordinates of vertex B by adding the height to the y-coordinate of the midpoint:
B(a,√3a)
Step 5: Summarize the Coordinates
Now we have the coordinates of all three vertices of the equilateral triangle:
- Vertex O at O(0,0)
- Vertex A at A(2a,0)
- Vertex B at B(a,√3a)
Final Coordinates
Thus, the coordinates of the vertices of the equilateral triangle are:
- O(0,0)
- A(2a,0)
- B(a,√3a)
---
We will place one vertex of the triangle at the origin, O(0,0). The other two vertices will be positioned based on the properties of an equilateral triangle.
Since one side of the triangle is horizontal, we can place vertex A at a distance of 2a along the x-axis from the origin. Therefore, the coordinates of vertex A will be:
A(2a,0)
The height h of an equilateral triangle can be calculated using the formula:
h=√32×side
For our triangle, the side length is 2a:
h=√32×2a=√3a
Vertex B will be positioned directly above the midpoint of the base OA. The midpoint of OA can be calculated as:
Midpoint=(0+2a2,0+02)=(a,0)
Now, we can find the coordinates of vertex B by adding the height to the y-coordinate of the midpoint:
B(a,√3a)
Now we have the coordinates of all three vertices of the equilateral triangle:
- Vertex O at O(0,0)
- Vertex A at A(2a,0)
- Vertex B at B(a,√3a)
Thus, the coordinates of the vertices of the equilateral triangle are:
- O(0,0)
- A(2a,0)
- B(a,√3a)
Topper's Solved these Questions
Similar Questions
Three charges Q,(+q) and (+q) are placed at the vertices of an equilateral triangle of side l as shown in the figure. It the net electrostatic energy of the system is zero, then Q is equal to

View SolutionThree charges Q,(+q) and (+q) are placed at the vertices of an equilateral triangle of side l as shown in the figure. It the net electrostatic energy of the system is zero, then Q is equal to

View Solution
Knowledge Check
Three masses each of mass m are palced at the vertices of an equilateral triangles ABC of side l as shown in figure. The force acting on a mass 2m placed at the centroid O of the triangle is
 AzeroB3Gm2l2C5Gm2l2D7Gm2l2
AzeroB3Gm2l2C5Gm2l2D7Gm2l2
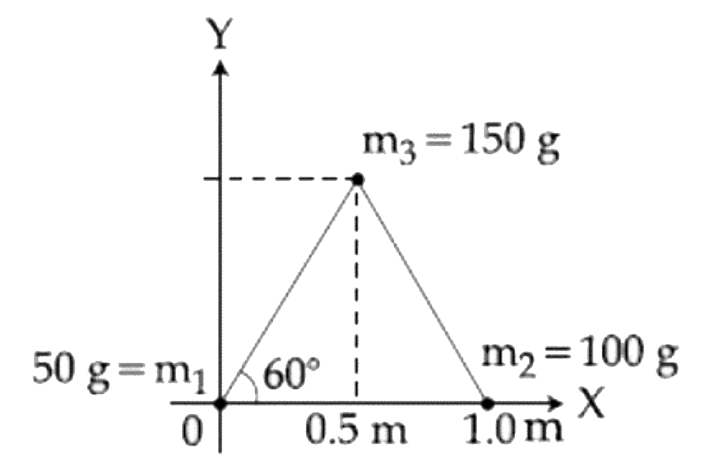
Three particles of massses 50 g, 100 g and 150 g are placed at the vertices of an equilateral triangle of side 1m ( as shown in the figure ) . The ( x, y) coordinates of the centre of mass will be :
View SolutionThree particles, each of mass m are situated at the vertices of an equilateral triangle ABC of side L as shown in the figure. Find the moment of inertia of the system about the line AX perpendicular to AB in the plane of ABC

View SolutionHow much work has to be done in assembling three charged particles at the vertices of an equilateral triangle as shown in figure

View SolutionFind the altitude of an equilateral triangle of side 8 cm.
View SolutionThree particles, each of mass m are situated at the vertices of an equilateral triangle ABC of side l (as shown in the figure).
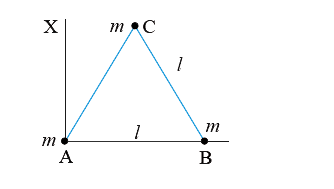
The moment of inertia of the system about a line AX perpendicular to AB and in the plane of ABC, will be:
View SolutionFind the perimeter of an equilateral triangle of side 13 cm.
View SolutionFind the area of an equilateral triangle whose side is a cm.
View Solution
