Three charges q, q, and -2q are fixed on the vertices of an equilateral triangular plate of edge length a. This plate is in equilibrium between two very large plates having surfaces charge density σ1andσ2, respectively. Find the time period of small anglular oscillations about an axis passing through its centroid and perpendicular to the plane. Moment of inertia of the system about this axis is l.
2π√ε0lqa|σ1−σ2|
2π√ε0l2qa|σ1−σ2|
2π√2ε0l√3qa|σ1−σ2|
2π√2ε0lqa|σ1−σ2|
The correct Answer is:C
To solve the problem, we need to find the time period of small angular oscillations of a system of three charges arranged in an equilateral triangle, placed between two charged plates. Here’s a step-by-step solution:
Step 1: Understand the Configuration
We have three charges: q, q, and −2q located at the vertices of an equilateral triangle with side length a. The triangle's centroid will be the axis about which we are considering the oscillations.
Step 2: Calculate the Dipole Moment
The dipole moment →P can be calculated for the system. The dipole moment due to two charges q and −q can be calculated as:
→P=q⋅→d
where →d is the vector from the negative charge to the positive charge. For our configuration, we have two dipoles formed by the pairs of charges (q,−2q) and (q,−2q).
Step 3: Calculate the Net Dipole Moment
Since the triangle is equilateral, the angle between the two dipoles is 60∘. The net dipole moment P can be calculated using the formula:
Pnet=√P21+P22+2P1P2cos(60∘)
Substituting cos(60∘)=12, we find:
Pnet=√P2+P2+P2=√3P
where P=q⋅a.
Step 4: Electric Field Between the Plates
The electric field E between two plates with surface charge densities σ1 and σ2 is given by:
E=σ1−σ22ϵ0
where ϵ0 is the permittivity of free space.
Step 5: Calculate the Torque
The torque τ on the dipole in an electric field is given by:
τ=→P×→E=PEsin(θ)
For small angles, sin(θ)≈θ.
Step 6: Relate Torque to Angular Acceleration
Using Newton's second law for rotation, we have:
τ=Iα
where I is the moment of inertia and α is the angular acceleration. Thus:
PEθ=Iα
Step 7: Time Period of Oscillation
The time period T for small oscillations is given by:
T=2π√Iτ
Substituting τ=PE gives us:
T=2π√IPE
Step 8: Substitute Values
Substituting P=√3qa and E=σ1−σ22ϵ0:
T=2π
⎷I√3qa⋅σ1−σ22ϵ0
This simplifies to:
T=2π√2ϵ0I√3qa|σ1−σ2|
Final Answer
The time period of small angular oscillations about the centroid is:
T=2π√2ϵ0I√3qa|σ1−σ2|
We have three charges: q, q, and −2q located at the vertices of an equilateral triangle with side length a. The triangle's centroid will be the axis about which we are considering the oscillations.
The dipole moment →P can be calculated for the system. The dipole moment due to two charges q and −q can be calculated as:
→P=q⋅→d
where →d is the vector from the negative charge to the positive charge. For our configuration, we have two dipoles formed by the pairs of charges (q,−2q) and (q,−2q).
Since the triangle is equilateral, the angle between the two dipoles is 60∘. The net dipole moment P can be calculated using the formula:
Pnet=√P21+P22+2P1P2cos(60∘)
Substituting cos(60∘)=12, we find:
Pnet=√P2+P2+P2=√3P
where P=q⋅a.
The electric field E between two plates with surface charge densities σ1 and σ2 is given by:
E=σ1−σ22ϵ0
where ϵ0 is the permittivity of free space.
The torque τ on the dipole in an electric field is given by:
τ=→P×→E=PEsin(θ)
For small angles, sin(θ)≈θ.
Using Newton's second law for rotation, we have:
τ=Iα
where I is the moment of inertia and α is the angular acceleration. Thus:
PEθ=Iα
The time period T for small oscillations is given by:
T=2π√Iτ
Substituting τ=PE gives us:
T=2π√IPE
Substituting P=√3qa and E=σ1−σ22ϵ0:
T=2π
⎷I√3qa⋅σ1−σ22ϵ0
This simplifies to:
T=2π√2ϵ0I√3qa|σ1−σ2|
The time period of small angular oscillations about the centroid is:
T=2π√2ϵ0I√3qa|σ1−σ2|
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Assertion and Reason Type8videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Comprehension Type94videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type2videos
MAGNETIC FIELD AND MAGNETIC FORCES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer12videos
MISCELLANEOUS VOLUME 5
Similar Questions
A disc of mass m, radius r and carrying charge q, is rotating with angular speed ω about an axis passing through its centre and perpendicular to its plane. Calculate its magnetic moment
View SolutionA disc of mass m, radius r and carrying charge q, is rotating with angular speed ω about an axis passing through its centre and perpendicular to its plane. Calculate its magnetic moment
View SolutionTwo discs have same mass and thickness. Their materials are of densities d1andd2. The ratio of their moments of inertia about an axis passing through the centre and perpendicular to the plane is
View SolutionFind the moment of inertia of a uniform square plate of mass M and edge of length 'l' about its axis passing through P and perpendicular to it.
 View Solution
View SolutionFind the moment of inertia of a uniform rectangular plate of mass M and edges of length 'I' and 'b' about its axis passing through the centre and perpendicular to it.
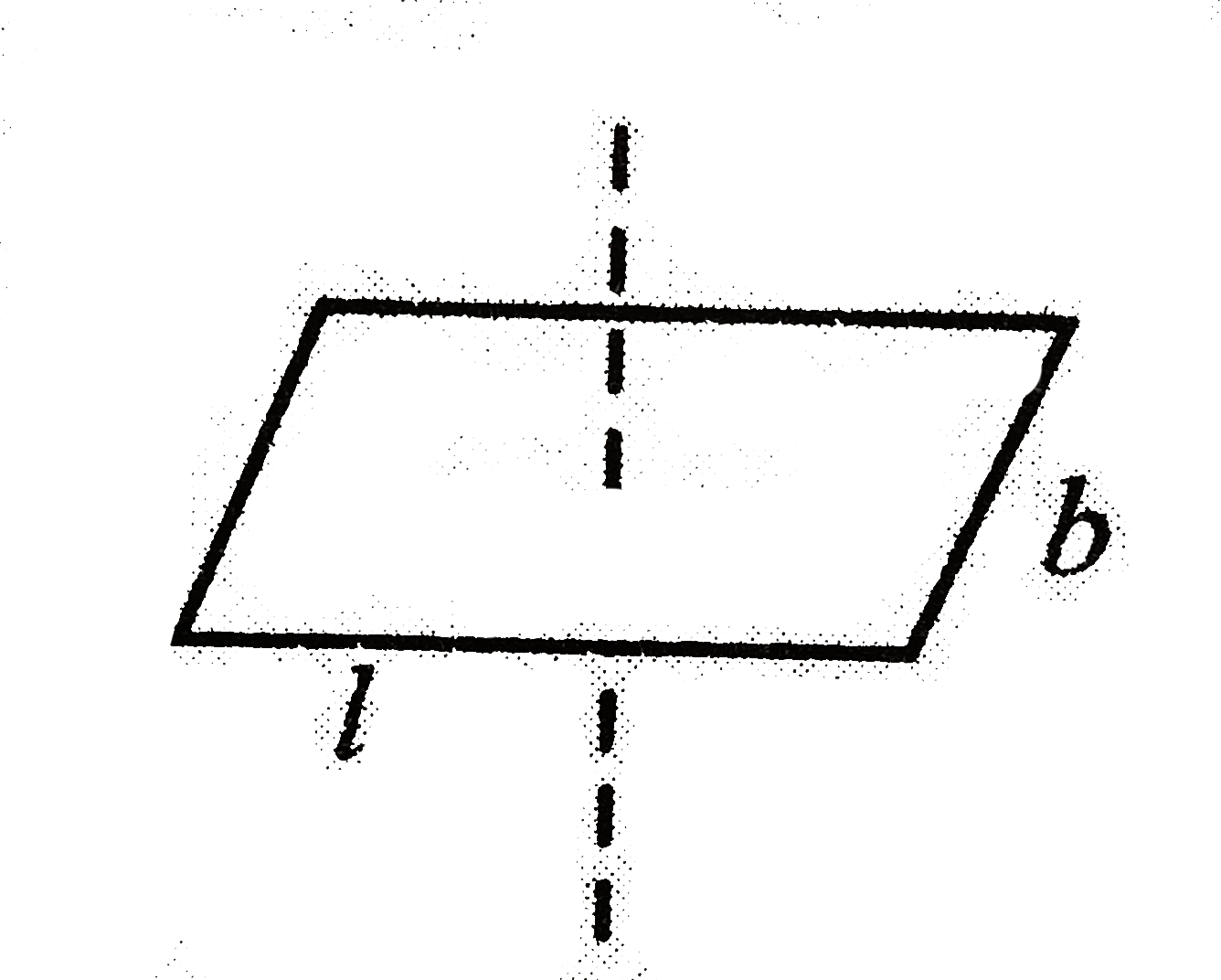 View Solution
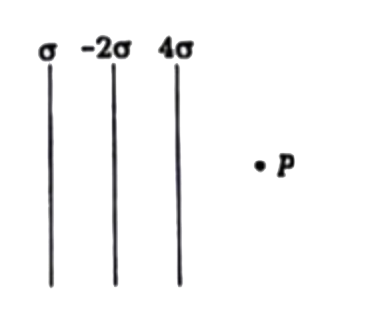
View SolutionThree non-conducting large parallel plates have surface charge densities σ,−2σand4σ respectively as shown in the figure. The electric field at the point P is
 View Solution
View SolutionThe surface mass density of a disc of radius a varies with radial distance as σ=A+Br where A & B are positive constants then moment of inertia of the disc about an axis passing through its centre and perpendicular to the plane
View SolutionIn the figure shown find the moment of inertia of square plate having mass m and sides a. About an axis 2 passing through point C (centre of mass) and in the plane of plate?
 View Solution
View Solution
Three rods each of mass m and length l are joined together to form an equilateral triangle as shown in figure. Find the moment of inertial of the system about an axis passing through its centre of mass and perpendicular to the plane of the particle.View SolutionA charge q is uniformly distributed on a non-conducting disc of radius R. It is rotated with an angular speed co about an axis passing through the centre of mass of the disc and perpendicular to its plane. Find the magnetic moment of the disc.
View Solution
