Three circular concentric wires of radii a, 2a and 3a are carrying currents 3l, 2l and l in same manner. Find the magnetic field at the common centre.
13μ0I6a
μ0I6a
μ0Ia
None of these
The correct Answer is:a
B=B1+B2+B3
=μ0(3l)2a+μ0(2l)2(2a)+μ0l2(3a)
=3μ0l2a+μ0l2a+μ0l6a
=9μ0l+3μ0l+μ0l6a=13μ0l6a

Topper's Solved these Questions
Similar Questions
The current-loop PQRSTP formed by two circular segments of radii R1 and R2 carries a current of I ampers. Find the magnetic field at the common centre O. what will be the field if angle α=90∘ ?
View SolutionA wire loop formed by joining two semicircular wires of radii R1 and R2 carries a current I as shown in figure. Find the magnetic field induction at the centre O.

View Solution
Knowledge Check
An otherwise infinite, straight wire has two concentric loops of radii a and b carrying equal currents in opposite directions as shown in Fig. The magnetic field at the common centre is zero for
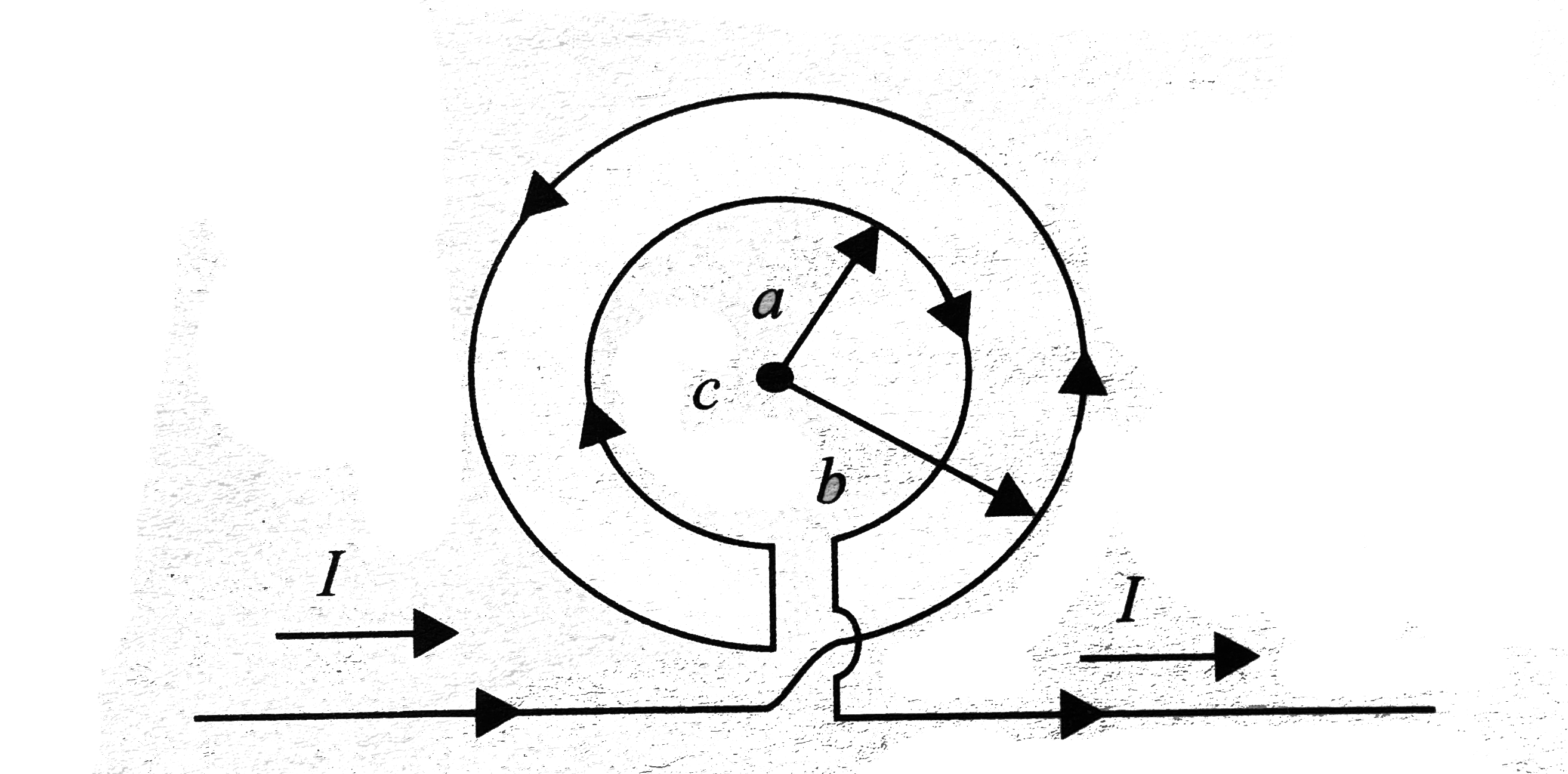 Aab=π−1πBab=ππ+1Cab=π−1π+1Dab=π+1π−1
Aab=π−1πBab=ππ+1Cab=π−1π+1Dab=π+1π−1A wire of length L carrying a current I is bent into a circle. The magnitude of the magnetic field at the centre of the circle is
Aπμ0ILBμ0I2LC2πμ0ILDμ0I2πLA wire of length L carrying a current I is bent into a circle. The magnitude of the magneitc field at the centre of the circle is
Aπμ0ILBμ0I2LC2πμ0ILDμ0I2πL
In the figure-4.30 shown two circular arcs are joined to make a closed loop carrying current l. Frnd the magnetic induction at the common centre 0.

View SolutionA circular loop of radius 9.7 cm carries a current 2.3 A. Obtain the magnitude of the magnetic field at the centre of the loop .
View SolutionFind the magnetic field induction at a point on the axis of a circular coil carrying current and hence find the magnetic field at the centre of circular coil carrying current.
View SolutionTwo concentric circular coils of five turns each are situated in the same plane. Their radii are 20 cm and 30 cm and they carry respectively 0.2 A and 0.3 A current in same direction. The magnetic field in tesla at the centre is
View SolutionTwo concentric circular coils often tums each are situated in the same plane. Their radii are 20 cm and 40 cm and they carry currents 0.2 A and 0.3 A respectively in opposite directions. The magnetic field in tesla at the centre is
View Solution
