Three conducting concentric spherical shells of radii R, 2R and 3R carry some charge on them. The potential at the centre is 50 V and that of middle and outer shell is 20 V and 10 V respectively. Find the potential of the inner Shell.
The correct Answer is:50V
To solve the problem of finding the potential of the inner shell in a system of three concentric spherical shells, we can follow these steps:
Given:
- Radii of the shells: R,2R,3R
- Potential at the center (inner shell): Vcenter=50V
- Potential of the middle shell: Vmiddle=20V
- Potential of the outer shell: Vouter=10V
Step 1: Understand the potential due to spherical shells
The potential V at a distance r from the center of a charged spherical shell is given by the formula:
V=kQr
where k is the Coulomb's constant and Q is the charge on the shell. For a conducting shell, the potential inside the shell is constant and equal to the potential at its surface.
Step 2: Set up equations for potentials
1. At the center (0 distance from the center):
Vcenter=kQ1R+kQ22R+kQ33R=50V(Equation 1)
2. At the surface of the middle shell (2R):
Vmiddle=kQ12R+kQ22R+kQ33R=20V(Equation 2)
3. At the surface of the outer shell (3R):
Vouter=kQ13R+kQ23R+kQ33R=10V(Equation 3)
Step 3: Solve the equations
From the equations above, we can express the potentials in terms of the charges Q1,Q2,Q3.
1. From Equation 1:
k(Q1R+Q22R+Q33R)=50
2. From Equation 2:
k(Q12R+Q22R+Q33R)=20
3. From Equation 3:
k(Q13R+Q23R+Q33R)=10
Step 4: Analyze the potential of the inner shell
Since the inner shell is a conductor, the potential inside it is uniform and equal to the potential at its surface. Therefore, the potential of the inner shell is equal to the potential at the center, which is already given as 50V.
Conclusion
Thus, the potential of the inner shell is:
Potential of the inner shell=50V
- Radii of the shells: R,2R,3R
- Potential at the center (inner shell): Vcenter=50V
- Potential of the middle shell: Vmiddle=20V
- Potential of the outer shell: Vouter=10V
The potential V at a distance r from the center of a charged spherical shell is given by the formula:
V=kQr
where k is the Coulomb's constant and Q is the charge on the shell. For a conducting shell, the potential inside the shell is constant and equal to the potential at its surface.
1. At the center (0 distance from the center):
Vcenter=kQ1R+kQ22R+kQ33R=50V(Equation 1)
Vmiddle=kQ12R+kQ22R+kQ33R=20V(Equation 2)
Vouter=kQ13R+kQ23R+kQ33R=10V(Equation 3)
From the equations above, we can express the potentials in terms of the charges Q1,Q2,Q3.
k(Q1R+Q22R+Q33R)=50
k(Q12R+Q22R+Q33R)=20
k(Q13R+Q23R+Q33R)=10
Since the inner shell is a conductor, the potential inside it is uniform and equal to the potential at its surface. Therefore, the potential of the inner shell is equal to the potential at the center, which is already given as 50V.
Thus, the potential of the inner shell is:
Potential of the inner shell=50V
Topper's Solved these Questions
- ELECTROSTATICSBOOK - ARIHANTCHAPTER - ELECTROSTATICSEXERCISE - Level 2
77 Videos
- ELECTROSTATICSBOOK - ARIHANTCHAPTER - ELECTROSTATICSEXERCISE - Level 3
59 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - ARIHANTCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 3
12 Videos
- GEOMETRICAL OPTICSBOOK - ARIHANTCHAPTER - GEOMETRICAL OPTICSEXERCISE - Level 3
9 Videos
Similar Questions
There are three conducting and concentricspherical shells of radii R,2R and 3R. The charge on inner and outer most shells are q and 3q while middle shell is earthed. Find the ratio of number of field lines emitted by outermost shell and inner shell.
View SolutionTwo conducting hollow spherical shells of radius R and 2R carry charges -Q and 3Q respectively. How much charge will flow into the earth if inner shell is grounded?
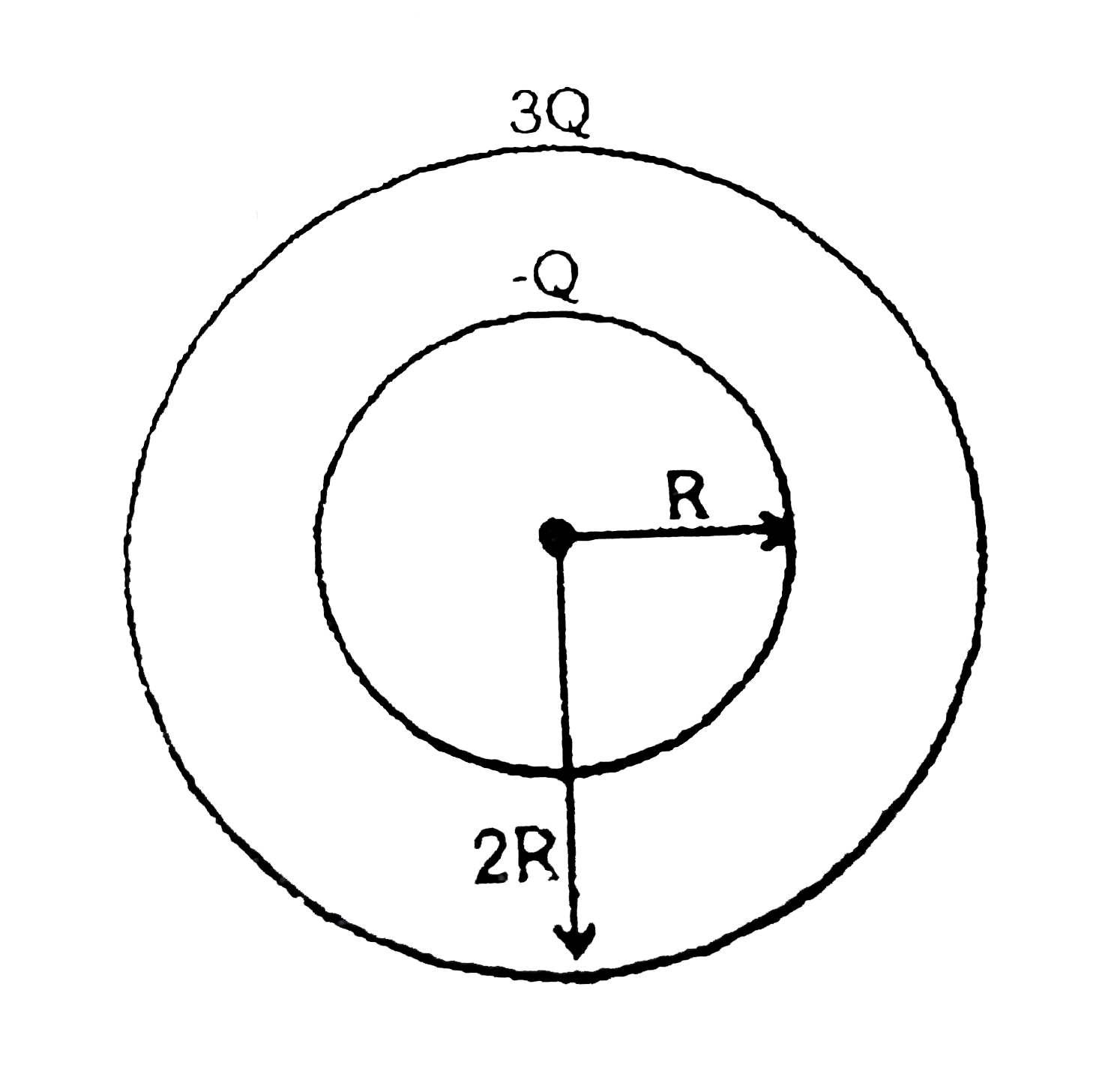
View Solution
Knowledge Check
If the electric potential of the inner shell is 10V and that of the outer shel is 5V, then the potential at the centre will be
 A10VB5VC15VDzero
A10VB5VC15VDzeroThere are two concentric conducting shells. The potential of outer shell is 10 V and that of inner shell is 15 V. If the outer shell is grounded, the potential of inner shell becomes / remains.
A25 VB15 VC10 VD5 VA spherical shell of radius 10 cm is carrying a charge q. If the electric potential at distances 5 cm, 10 cm and 15 cm from the centre of the spherical shell is V1,V2 and V3 respectively, then
AV1=V2>V3BV1>V2>V3CV1=V2<V3DV1<V2<V3
There are two concentric conducting spherical shells of radii 10 cm and 20 cm. The outer shell is charged to a potential of 50esu while inner shell is earthed. The charge on outer shell is
View SolutionThree concentric conducting spherical shells of radii R,2R and 3R carry charges Q,−2Q and 3Q, respectively.
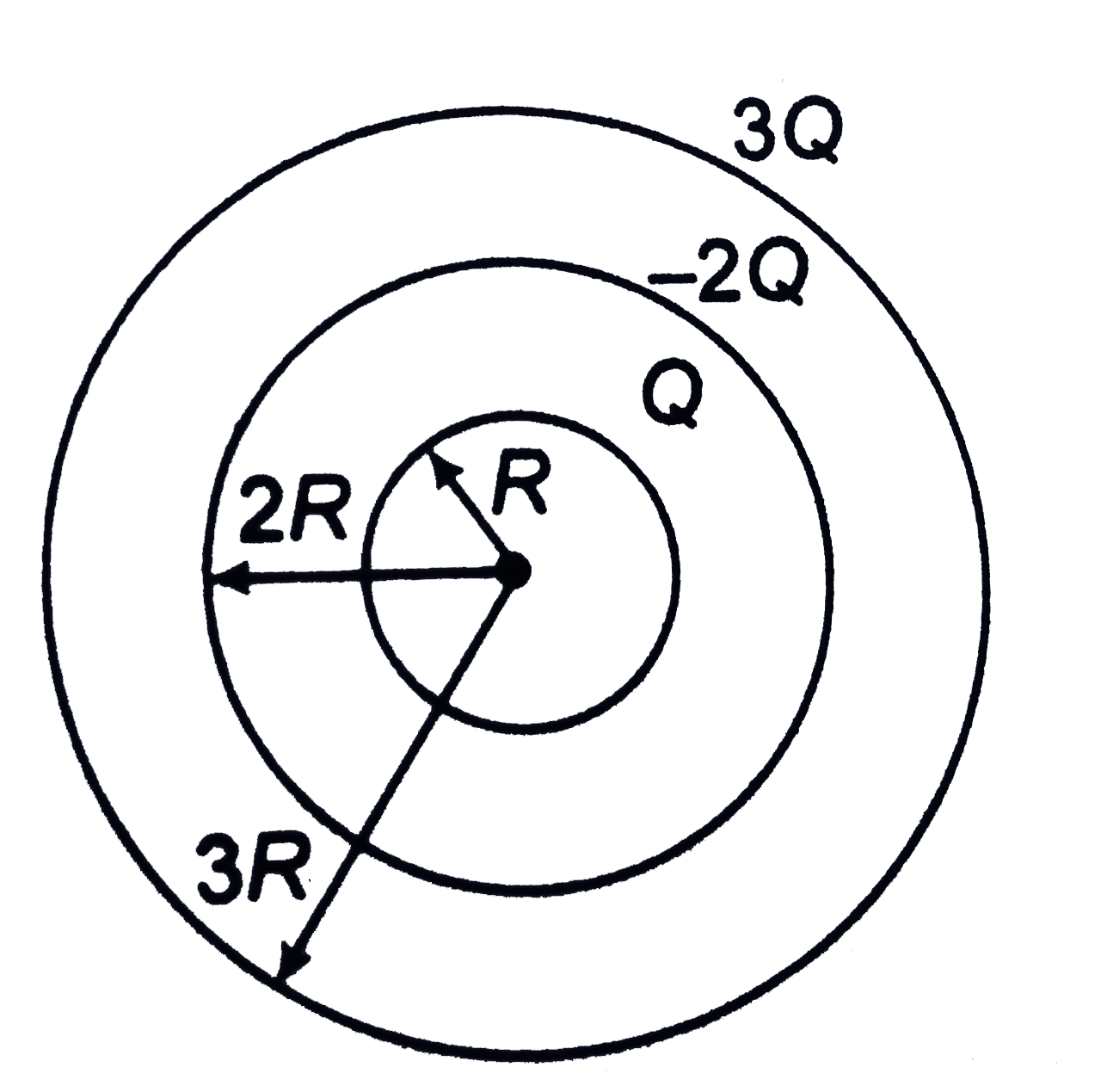
a. Find the electric potential at r=R and r=3R where r is the radial distance from the centre. ltbr> b. Compute the electric field at r=52R
c.computethe→tale≤ctrostatice≠rgys→red∈thesystem.<br>The∈≠rshellisnowco∩ected→theexternalo≠byaconduct∈gwire,passingthroughaverysmallho≤∈them≤shell.<br>Computethechar≥sonthespheresofradiiRand3R.<br>e.Computethee≤ctricfieldatr=5/2R.
View SolutionTwo concentric spherical conducting shells of radii R and 2R carry charges Q and 2Qrespectively.Change in electric potential on the outer shell when both are connected by a conducting wire is (k=14πɛ0)
View SolutionTwo concentric conducting spherical shells of radii a1anda2(a2>a1) are charged to potentials ϕ1 and ϕ2, respectively. Find the charge on the inner shell.
View SolutionTwo uniformly charged concentric spherical shells of radius R and r, are given charges Q1 and Q2 respectively. If their potential difference is V, then it will not depends upon:

View Solution
