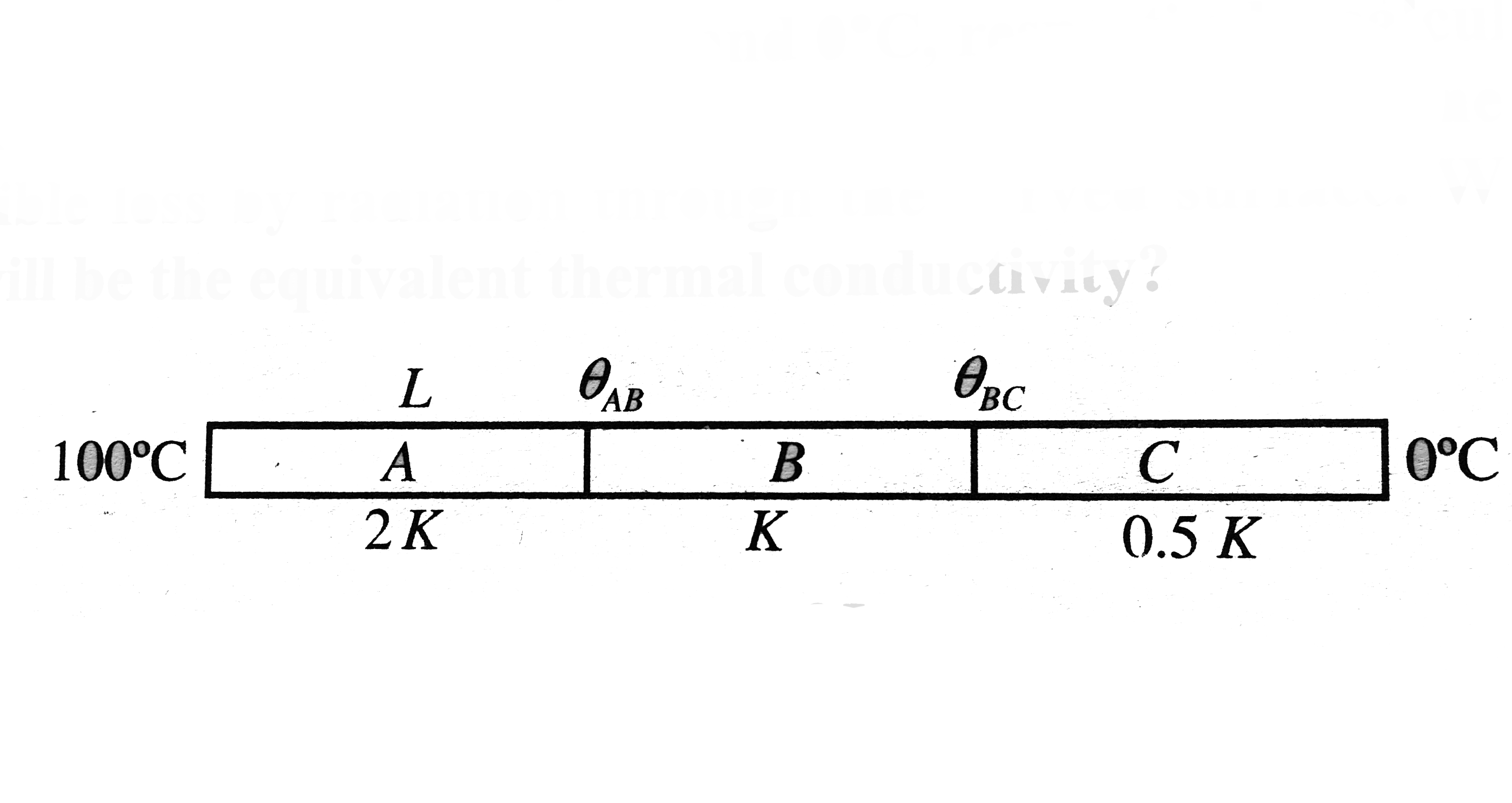
Three cylindrical rods A, B and C of equal lengths and equal diameters are joined in series as shown if Fig. Their thermal conductivities are 2K, K and 0.5K, respectively. In steady state, if the free ends of rods A and C are at 100∘C and 0∘C, respectively, calculate the temperature at the two junction points. Assume negligible loss by radiaiotn through the curved surface. What will be the equivalent thermal conductivity?
As the rods are in series, Req=RA+RB+RC with R=(LKA)
Req=L2KA+LKA+L0.5KA=7L2KA ..(i)
and hence, H=dQdt=ΔθR=(100−0)7L2KA=200KA7L
Now in series, rate of flow of heat remains same i.e.,
H=HA=HB=HC.
So for rod A, [dQdt]A=[dQdt]
i.e., (100−θAB)2KAL=200KAL
θBC=(4007)=57.1∘C
Furthermore, if Keq is equivalent thermal conductivity,
Req=L+L+LKeqA=7L2KA
Keq=(6/7)K
Topper's Solved these Questions
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Exercise 1.1
23 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Exercise 1.2
22 Videos
- BASIC MATHEMATICSBOOK - CENGAGE PHYSICSCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise 2.6
20 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
Three identical rods are joined in series as shown. Their thermal conductivities are K,K/2 and K/3 respectively. At steady, if the free ends of rods are at 100∘C and 20∘C respectively. Determine the temperature at two junction points. Also find the equivalent thermal conductivity.
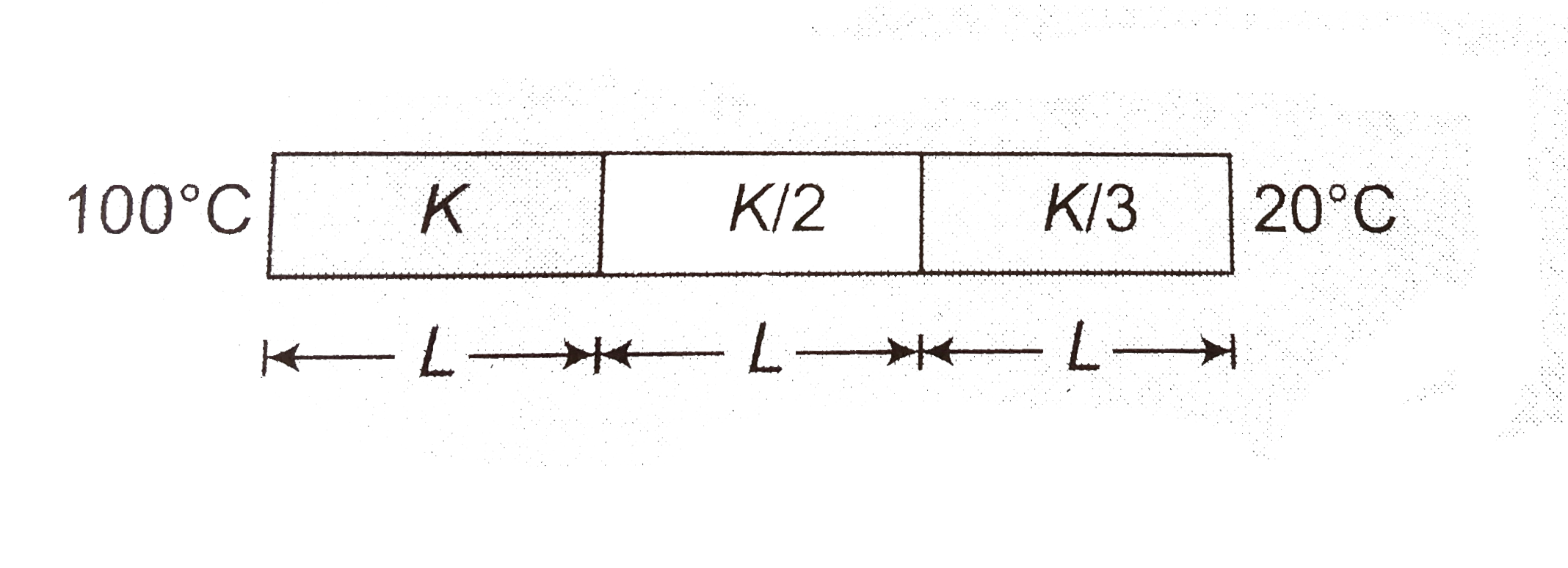
View SolutionThree bars of equal lengths and equal area of cross-section are connected in series fig. their thermal conducitives are in the ratio 2:3:4. If at the steady state the open ends of the first and the last bars are at temperature 200∘C and 20∘C respectively, find the temperature of both the junctions.
 .
.
View Solution
Knowledge Check
Three rods A, B and C of the same length and same cross-sectional area are joined as shown. Their thermal conductivities are in the ratio 1:2:3/2. If the open ends of A and C are at 200∘C and 18∘C, respectively, then the temperature at the junction of A at steady state is
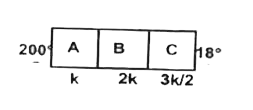 A156∘CB148∘CC116∘CD74∘C
A156∘CB148∘CC116∘CD74∘CTwelve conducting rods from the sides of a uniform cube of side l. If in steady state, B and H ends of the cube are at 100∘C and 0∘C respectively. Find the temperature of the junction 'A' :-
_E01_117_Q01.png) A80∘CB60∘CC40∘CD70∘C
A80∘CB60∘CC40∘CD70∘CThree rods A,B and C of the same length and cross- sectional area are joined in series as shown. The temperature at the junction of A and B, in equilibriu, is
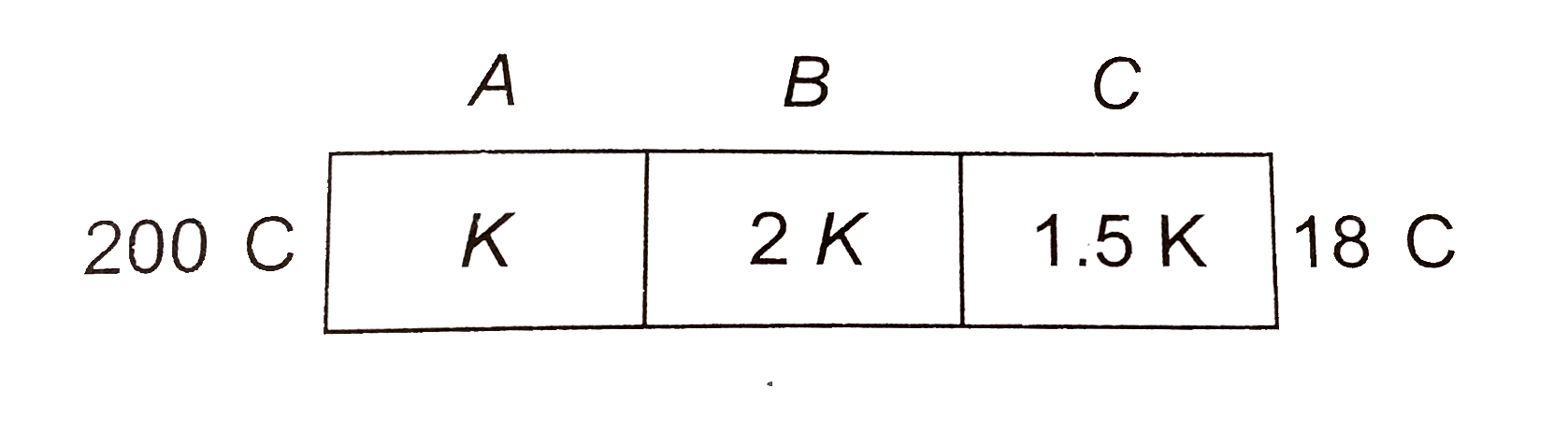 A74∘CB116∘CC156∘CD148∘C
A74∘CB116∘CC156∘CD148∘C
Three bars of equal lengths x and equal area of cross-section A are connected in series. Their thermal conductivities are in the ratio 2:4:3. If the open ends of the first and the last bars are at temperatures 200∘C and 18∘C, respectively in the steady state, calculate the temperatures of both the junctions.
View SolutionThree bars of equal lenghts and equal area of cross-section are connected in series. Their thermal conductivities are in the ratio of 2:4:3. If the open ends of the first and the last bars are at temperature 200∘C and 180∘C respectivity in the steady state, calculate the temperature of both the junctions.
View SolutionThree rods each of same length and cross - section are joined in series. The thermal conductivity of the materials are K, 2K and 3K respectively. If one end is kept at 200∘C and the other at 100∘C. What would be the temperature of the junctions in the steady state? Assume that no heat is lost due to radiation from the sides of the rods.
View SolutionThree rods of same dimension are joined in series having thermal conductivity k1 , k2 and k3. The equivalent thermal conductivity is
View SolutionIn a steady state of thermal conduction, temperature of the ends A and B of a 20 cm long rod are 100∘C and 0∘C respectively. What will be the temperature of the rod at a point at a distance of 6 cm from the end A of the rod
View Solution
