Three rods of same dimension are joined in series having thermal conductivity k1 , k2 and k3. The equivalent thermal conductivity is
k1k2k3/k2k3+k1k2+k1k3
3(k1k2k3)/k2k3+k1k2+k1k3
k1+k2+k3
(k1+k2+k3)/ 3
The correct Answer is:B
To find the equivalent thermal conductivity of three rods joined in series with thermal conductivities k1, k2, and k3, we can follow these steps:
1. Understanding the Setup:
We have three rods of the same dimensions (length L and cross-sectional area A) connected in series. The thermal conductivities of the rods are k1, k2, and k3.
2. Thermal Resistance Calculation:
The thermal resistance R for each rod can be calculated using the formula:
R=LkA
Therefore, the thermal resistances for the three rods will be:
- For rod 1: R1=Lk1A
- For rod 2: R2=Lk2A
- For rod 3: R3=Lk3A
3. Total Thermal Resistance in Series:
Since the rods are in series, the total thermal resistance Req is the sum of the individual resistances:
Req=R1+R2+R3=Lk1A+Lk2A+Lk3A
4. Factor Out Common Terms:
We can factor out LA from the equation:
Req=LA(1k1+1k2+1k3)
5. Finding Equivalent Conductivity:
The equivalent thermal conductivity keq can be defined in terms of the equivalent resistance:
Req=LkeqA
Setting the two expressions for Req equal gives:
LkeqA=LA(1k1+1k2+1k3)
6. Solving for keq:
Canceling LA from both sides, we have:
1keq=1k1+1k2+1k3
Taking the reciprocal gives:
keq=1(1k1+1k2+1k3)
7. Finding a Common Denominator:
To express keq in a more usable form, we can find a common denominator:
keq=k1k2k3k2k3+k1k3+k1k2
Final Answer:
Thus, the equivalent thermal conductivity keq for the three rods in series is:
keq=3k1k2k3k1k2+k2k3+k3k1
We have three rods of the same dimensions (length L and cross-sectional area A) connected in series. The thermal conductivities of the rods are k1, k2, and k3.
The thermal resistance R for each rod can be calculated using the formula:
R=LkA
Therefore, the thermal resistances for the three rods will be:
- For rod 1: R1=Lk1A
- For rod 2: R2=Lk2A
- For rod 3: R3=Lk3A
Since the rods are in series, the total thermal resistance Req is the sum of the individual resistances:
Req=R1+R2+R3=Lk1A+Lk2A+Lk3A
We can factor out LA from the equation:
Req=LA(1k1+1k2+1k3)
The equivalent thermal conductivity keq can be defined in terms of the equivalent resistance:
Req=LkeqA
Setting the two expressions for Req equal gives:
LkeqA=LA(1k1+1k2+1k3)
Canceling LA from both sides, we have:
1keq=1k1+1k2+1k3
Taking the reciprocal gives:
keq=1(1k1+1k2+1k3)
To express keq in a more usable form, we can find a common denominator:
keq=k1k2k3k2k3+k1k3+k1k2
Thus, the equivalent thermal conductivity keq for the three rods in series is:
keq=3k1k2k3k1k2+k2k3+k3k1
Topper's Solved these Questions
Similar Questions
Five rods of same dimensions are arranged as shown in the figure. They have thermal conductivities k1,k2,k3andk5. When points A and C are maintained at different temperature, no heat flows through the central rod if
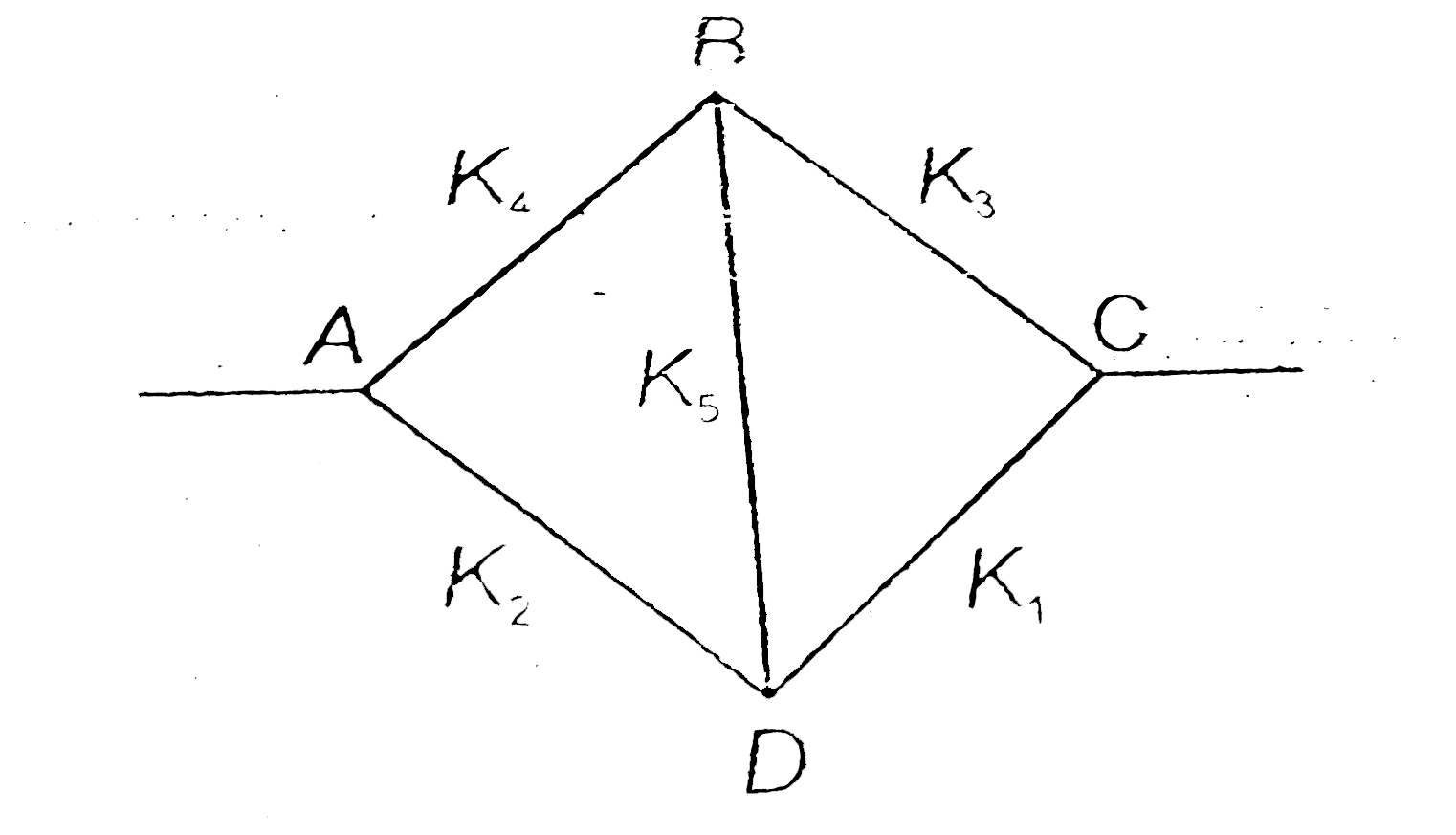
View Solution Statement I: Two solid cylindrical rods of identical size and different thermal conductivity K1 and K2 are connected in series. Then the equivalent thermal conductivity of two rods system is less than that value of thermal conductivity of either rod.
Statement I: Two solid cylindrical rods of identical size and different thermal conductivity K1 and K2 are connected in series. Then the equivalent thermal conductivity of two rods system is less than that value of thermal conductivity of either rod.
Statement II: For two cylindrical rods of identical size and different thermal conductivity K1 and K2 connected in series, the equivalent thermal conductivity K is given by 2K=1K1+1K2
View Solution
Knowledge Check
Two rods of the same length and diameter having thermal conductivities K1 and K2 are joined in parallel. The equivalent thermal conductivity of combination is
AK1K2K1+K2B(K1+K2)CK1+K22D√K1K2Two rods of the same length and diameter having thermal conductivities K1 and K2 are joined in parallel. The equivalent thermal conductivity of combination is
AK1K2K1+K2B(K1+K2)CK1+K22D√K1K2Two rods of the same length and diameter, having thermal conductivities K1 and K2, are joined in parallel. The equivalent thermal conductivity to the combinationk is
AK1K2K1+K2BK1K2CK1+K22D√K1K2
A slab consists of two layers of different materials of the same thickness and having thermal conductivities K1 and K2. The equivalent thermal conductivity of the slab is
View Solution
Three rods of same dimensions are arranged as shown in Fig. They have thermal conductivities K1,K2 and K3. The points P and Q are maintained at different temeperature for the heat to flow at the same rate along PRQ and PQ. Whi of the following options correct?
View SolutionA slab consists of two parallel layers of two different materials of same thickness having thermal conductivities K1andK2. The equivalent conductivity of the combination is
View SolutionThe thermal conductivity of a rod depends on
View SolutionConsider a compound slab consisting of two different material having equal thickness and thermal conductivities K and 2K respectively. The equivalent thermal conductivity of the slab is
View Solution