Three identical small spheres each of mass 0.1 g are suspended by three silk threads each of length 20 cm from a certain point. How much charge should be given to each sphere so that each thread will make an angle of 30∘ with the vertical? You may suppose that each sphere has equal charge.
The sphere are identical and each sphere has equal charge. They will repel each otherw with equal force. So in the positon of equilibrium they will form an equilateral triangle ABC in the horizontal plane. Here, length of the thread OA=OB=OC=20cm, mass of each sphere, m=0.1 g angle of inclination of the thread with the vertical, θ=30∘
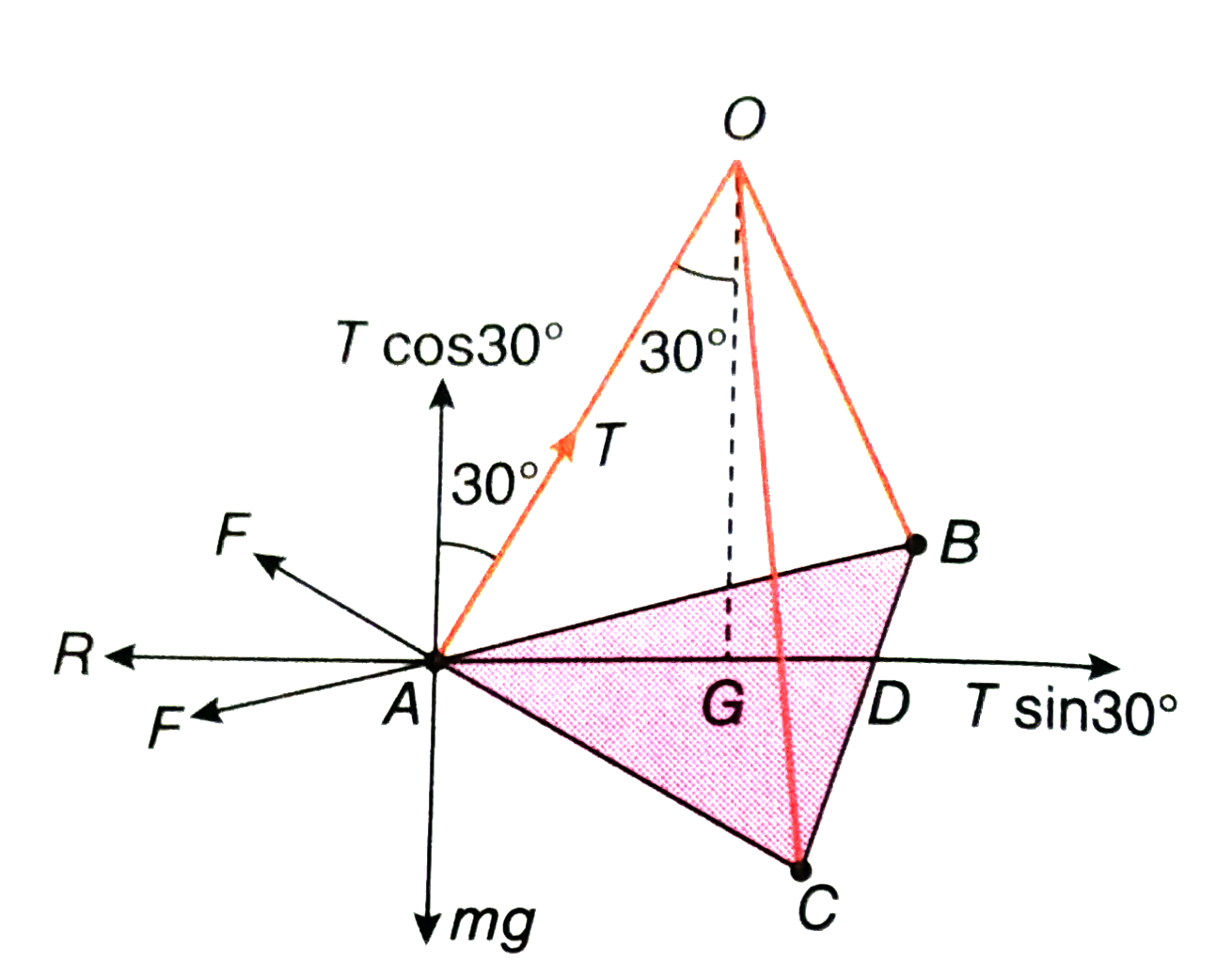
Suppose, charge of each sphere is q.
Clearly, the vertical line OG passes through the centre of gravity of the triangle ABC. Suppose , length of each side of the triangle =a
Median AD=√a2−(a24)=√32a
Now AG=23AD=23.√32a=a√3
Again sin30∘=AGOA or AG=OAsin30∘=20×12=10cm
∴a√3=10 or a=10√3cm
Force of repulsion between any two balls F=q2a2
On the sphere A two equal forces of repulsion F act due to the spheres B and C. Suppose, the resultant of these two equal forces is R.
∴R2=F2+F2+2F.Fcos60∘[∵∠BAC=602,
∴ internal angle between F and F=60∘]
=F2+F2+F2=3F2
or R=√3F=√3.q2a2
Let the tension along AO=T
∴ At equilibrium Tsin30∘=R and Tcos30∘=mg
∴tan30∘=Rmg=√3q2a2.mg
or 1√3=√3q2a2mg or q2=a2mg3
or q=a√mg3=10√3.√0.1×9803=99 esu (approx)
Topper's Solved these Questions
- ELECTRIC FIELDBOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC FIELDEXERCISE - SECTION RELATION QUESTIONS
50 Videos
- ELECTRIC FIELDBOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC FIELDEXERCISE - HIGHER ORDER THINKING SKILL QUESTIONS
33 Videos
- ELECTRIC ENERGY AND POWERBOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC ENERGY AND POWEREXERCISE - CBSE SCANNER
7 Videos
- ELECTRIC POTENTIAL BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC POTENTIAL EXERCISE - CBSE Scanner
13 Videos
Similar Questions
Three identical small balls, each of mass 0.1 g, are suspended at one point on silk thread having a length of l=20cm . What charges should be imparted to the balls for each thread to form an angle of α=30∘ with the vertical?
View SolutionThree identical small balls, each of mass 0.1 g, are suspended at one point on silk thread having a length of l=20cm . What charges should be imparted to the balls for each thread to form an angle of α=30∘ with the vertical?
View Solution
Knowledge Check
Two small balls of mass m each are suspended side by side by two equal threds to length L. If the distance between the upper ends of the threads be a, the angle θ that the threads will make with the vertical due to attraction between the balls is :
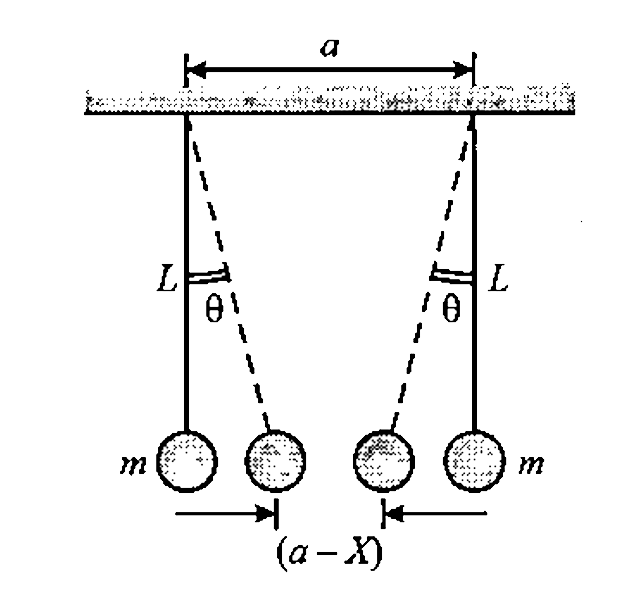 Atan−1(a−X)gmGBtan−1mG(a−X)2gCtan−1(a−X)2gmGDtan−1(a2−X2)gmG
Atan−1(a−X)gmGBtan−1mG(a−X)2gCtan−1(a−X)2gmGDtan−1(a2−X2)gmG
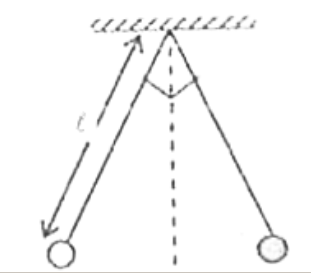
Two small metallic spheres each of mass 'm' are suspended together with strings of length 'l' and placed together. When a quantum of charge 'q' is transferred to each the strings make and angle of 90∘ with each other. The value of 'q' is
View SolutionTwo pith ball of mass 0.5 each are suspended from a common point O by means of silk threads, each of length 20 cm. When the balls are given equal and similar charges, they repel each other so that the two threads make an angle of 60∘ with each-other. Determine the charge on each ball.
View SolutionTwo small balls of mass m each are suspended side by side by two equal threds to length L. If the distance between the upper ends of the threads be a, the angle θ that the threads will make with the vertical due to attraction between the balls is :

View SolutionTwo small spheres each of mass 10−6 kg are suspended from a point by silkk threads 50cm long. They are equally chareged and repel each other to a distance 20cm apart. Calculate charege on each Take g=9.8ms−2.
View SolutionTwo small spheres each of mass m and charge q are tied from the same rigid support with the help of silk threads of length L. They make angle θ with the vertical as shown in the fig. If length L is decreased, then angle θ with the vertical.
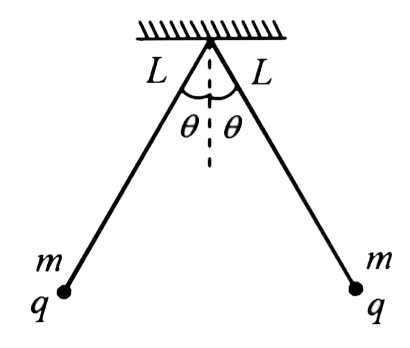
View SolutionTwo small spheres each of mass m and charge q are tied from the same rigid support with the help of silk threads of length L. They make angle θ with the vertical as shown in the fig. If length L is decreased, then angle θ with the vertical.

View Solution2 small spheres each of mass m and carrying +q coulomb, are suspended by massles insulating threads, each of length l. Prove that q2=(4mgl2sin2θtanθ)4πε0, where θ is angle made of strings with the vertical at equilibrium.
View Solution
