2 small spheres each of mass m and carrying +q coulomb, are suspended by massles insulating threads, each of length l. Prove that , where is angle made of strings with the vertical at equilibrium.
To solve the problem, we will analyze the forces acting on the two charged spheres and derive the required equation step by step.
Step 1: Analyze the Forces
Each sphere has a mass m and carries a charge +q. The forces acting on each sphere are:
- The gravitational force mg acting downwards.
- The tension T in the thread acting upwards at an angle θ with the vertical.
- The electrostatic repulsive force F between the two spheres.
Step 2: Set Up the Equilibrium Conditions
At equilibrium, the forces in both the vertical and horizontal directions must balance.
Vertical Direction:
The vertical component of the tension must balance the weight of the sphere:
Tcosθ=mg(1)
Horizontal Direction:
The horizontal component of the tension must balance the electrostatic repulsive force:
Tsinθ=F(2)
Step 3: Calculate the Electrostatic Force
The electrostatic force F between two charges is given by Coulomb's law:
F=kq2r2
where k=14πϵ0 and r is the distance between the two charges.
From geometry, the distance r between the two spheres can be expressed as:
r=2lsinθ
Thus, the electrostatic force becomes:
F=kq2(2lsinθ)2=kq24l2sin2θ(3)
Step 4: Substitute F into the Horizontal Force Equation
Substituting equation (3) into equation (2):
Tsinθ=kq24l2sin2θ
Step 5: Divide Equation (2) by Equation (1)
Now, we divide equation (2) by equation (1):
TsinθTcosθ=kq24l2sin2θmg
This simplifies to:
tanθ=kq24l2sin2θmg
Step 6: Rearranging to Find q2
Rearranging the above equation gives:
q2=4mgl2sin2θtanθk
Step 7: Substitute k
Substituting k=14πϵ0:
q2=4mgl2sin2θtanθ⋅4πϵ0
Thus, we arrive at the final result:
q2=(4mgl2sin2θtanθ)⋅4πϵ0
Final Result
We have proved that:
q2=4mgl2sin2θtanθ⋅4πϵ0
Each sphere has a mass m and carries a charge +q. The forces acting on each sphere are:
- The gravitational force mg acting downwards.
- The tension T in the thread acting upwards at an angle θ with the vertical.
- The electrostatic repulsive force F between the two spheres.
At equilibrium, the forces in both the vertical and horizontal directions must balance.
The vertical component of the tension must balance the weight of the sphere:
Tcosθ=mg(1)
The horizontal component of the tension must balance the electrostatic repulsive force:
Tsinθ=F(2)
The electrostatic force F between two charges is given by Coulomb's law:
F=kq2r2
where k=14πϵ0 and r is the distance between the two charges.
r=2lsinθ
Thus, the electrostatic force becomes:
F=kq2(2lsinθ)2=kq24l2sin2θ(3)
Substituting equation (3) into equation (2):
Tsinθ=kq24l2sin2θ
Now, we divide equation (2) by equation (1):
TsinθTcosθ=kq24l2sin2θmg
This simplifies to:
tanθ=kq24l2sin2θmg
Rearranging the above equation gives:
q2=4mgl2sin2θtanθk
Substituting k=14πϵ0:
q2=4mgl2sin2θtanθ⋅4πϵ0
Thus, we arrive at the final result:
q2=(4mgl2sin2θtanθ)⋅4πϵ0
We have proved that:
q2=4mgl2sin2θtanθ⋅4πϵ0
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - EVALUATE YOURSELF-110videos
ELECTRIC CHARGES AND FIELDS
- BOOK - NARAYNACHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - EVALUATE YOURSELF-29videos
ELECTRIC CHARGES AND FIELDS
- BOOK - NARAYNACHAPTER - DUAL NATUREEXERCISE - LEVEL-II (H.W)17videos
DUAL NATURE
- BOOK - NARAYNACHAPTER - ELECTRO MAGNETIC INDUCTIONEXERCISE - Level-II (H.W)23videos
ELECTRO MAGNETIC INDUCTION
Similar Questions
Two small spheres each of mass 'm' kg and charge q coulomb are suspended from a point by insulating threads each of 1 metre length, but of negliglible mass. If θ is the angle which each string makes with the verticle vertical when equilbrium has been reached, show that
q2=4mgl2sin2θtanθ(4π∈0)View SolutionProve that tan(π4+θ2)=secθ+tanθ
View Solution
Knowledge Check
- Question 1 - Select One
∫π/404sin2θdθsin4θ+cos4θ=
Aπ4Bπ2CπDNone of these
Prove that: cos2θ1+sin2θ=tan(π4−θ)
View SolutionTwo small spheres each of mass m and charge q are tied from the same rigid support with the help of silk threads of length L. They make angle θ with the vertical as shown in the fig. If length L is decreased, then angle θ with the vertical.
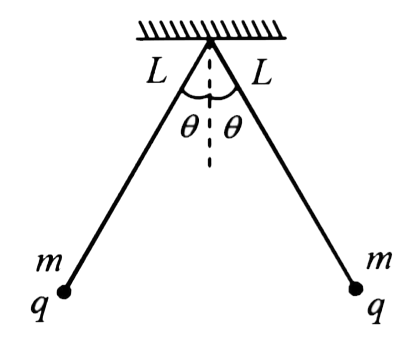 View Solution
View SolutionTwo similar balls, each of mass m and charge q, are hung from a common point by two slik threads, each of length l. Prove that separation between the ball is x=[q2l2πε0mg]1/3, if θ is small
Find the rate dqdt with which the charge should leak off each sphere if the velocity of approach varies as v=a/√x, where a is a constant.
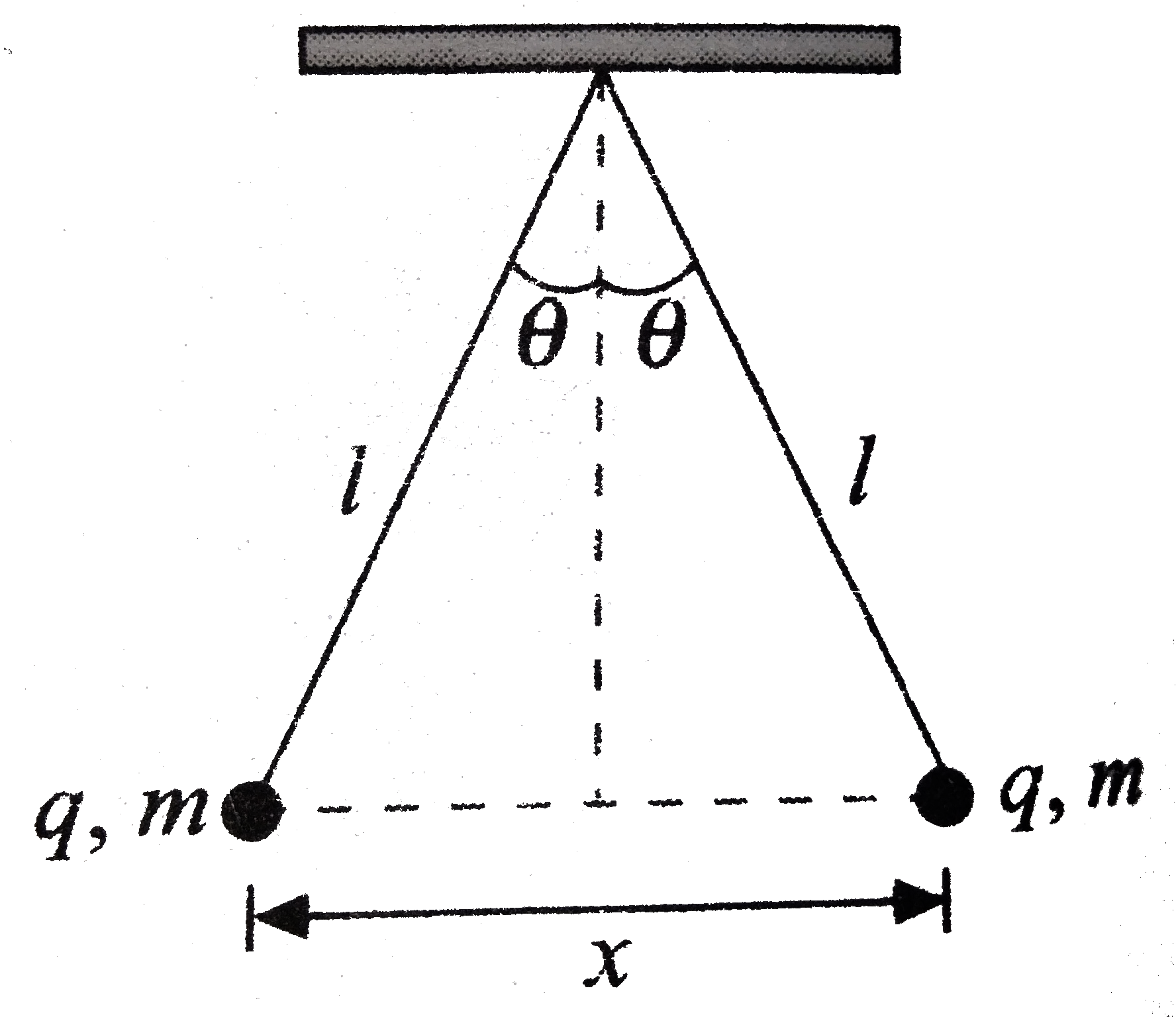 View Solution
View SolutionProve that secθ+tanθ=tan(π4+θ2)
View SolutionProve that 1+sinθ1−sinθ=tan2(π4+θ2)
View SolutionProve that sinθ<θ<tanθ for θ∈(0,π2).
View SolutionProve that:cos2(π4−θ)−sin2(π4−θ)=s∈2θ
View Solution

