Three particles each of 'm' are kept at the three vertices of an equilateral triangle of side 'a' . Moment of inertia of the system about an axis passing through the centroid and perpendicular to its plane is
3ma2
ma2
ma2/3
2/3ma2
The correct Answer is:B
To find the moment of inertia of a system of three particles each of mass 'm' located at the vertices of an equilateral triangle of side 'a', we follow these steps:
Step 1: Identify the Centroid of the Triangle
The centroid of an equilateral triangle is located at a point where the medians intersect. For an equilateral triangle, the centroid divides each median in a 2:1 ratio.
Step 2: Calculate the Distance from the Centroid to Each Vertex
For an equilateral triangle with vertices A, B, and C, the distance from the centroid (G) to any vertex (say A) can be calculated using the formula:
d=a√3
This is derived from the geometry of the triangle, where the median length is √32a and the distance from the centroid to a vertex is 23 of the median.
Step 3: Write the Moment of Inertia Formula
The moment of inertia I of a system of point masses is given by:
I=∑mir2i
where mi is the mass of each particle and ri is the distance from the axis of rotation (in this case, the centroid).
Step 4: Substitute Values into the Moment of Inertia Formula
Since all three masses are equal and the distances from the centroid to each vertex are the same, we can simplify the moment of inertia calculation:
I=3⋅m⋅d2
Substituting d=a√3:
I=3⋅m⋅(a√3)2
Step 5: Simplify the Expression
Calculating d2:
d2=(a√3)2=a23
Now substituting this back into the moment of inertia equation:
I=3⋅m⋅a23=m⋅a2
Final Result
Thus, the moment of inertia of the system about an axis passing through the centroid and perpendicular to its plane is:
I=ma2
The centroid of an equilateral triangle is located at a point where the medians intersect. For an equilateral triangle, the centroid divides each median in a 2:1 ratio.
For an equilateral triangle with vertices A, B, and C, the distance from the centroid (G) to any vertex (say A) can be calculated using the formula:
d=a√3
This is derived from the geometry of the triangle, where the median length is √32a and the distance from the centroid to a vertex is 23 of the median.
The moment of inertia I of a system of point masses is given by:
I=∑mir2i
where mi is the mass of each particle and ri is the distance from the axis of rotation (in this case, the centroid).
Since all three masses are equal and the distances from the centroid to each vertex are the same, we can simplify the moment of inertia calculation:
I=3⋅m⋅d2
Substituting d=a√3:
I=3⋅m⋅(a√3)2
Calculating d2:
d2=(a√3)2=a23
Now substituting this back into the moment of inertia equation:
I=3⋅m⋅a23=m⋅a2
Thus, the moment of inertia of the system about an axis passing through the centroid and perpendicular to its plane is:
I=ma2
Topper's Solved these Questions
Similar Questions
Three particles each of mass 12 g are located at the vertices of an equilateral triangle of side 10 cm. Calculate the moment of inertia of the system about an axis passing through the centroid and perpendicular to the plane of the triangle?
View SolutionThree particles, each of mass m are situated at the vertices of an equilateral triangle ABC of side L figure. Find thee moment of inertia of the system about the line AX perpendicular to AB in the plane of ABC

View Solution
Knowledge Check
The moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
Aincreases if its temperature is increasedBchanges if its axis of rotation is changedCincreases if its angular velocity is increasedDboth (a) and (b) are correctMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
A1/2MR2BMR2C1/4MR2D3/4MR2Three point masses each of mass m are placed at the corners of an equilateral triangle of side 'a'. Then the moment of inertia of this system about an axis passing along one side of the triangle is
Ama2B3ma2C34ma2D23ma2
Three particles each of mass m are placed on the vertices of an equilateral triangle of length L. Find the M.I.
(a) about an axis passing through
(i) one particle and perpendicular to the plane
(ii) mid-point of the side of triangle and ⊥ar to the plane
(iii) center of triangle and ⊥ar to the plane
(b) (i) an axis coinciding with side of triangle
(ii) about median of triangle
View SolutionFind the moment of inertia of a disk about an axis passing through a point on its circumference perpendicular to its plane.
View SolutionThree particles, each of mass m are situated at the vertices of an equilateral triangle ABC of side l (as shown in the figure).
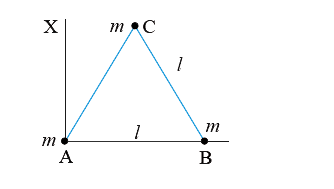
The moment of inertia of the system about a line AX perpendicular to AB and in the plane of ABC, will be:
View SolutionThree particles, each of mass 200 g are kept at the corners of an equilateral triangle of side 10 cm. Find the moment of inertia of the system about an axis
a. joining two of the particles and
passing through lone of the particle and perpendicular to the plane of the particles.
View SolutionThree identical uniform thin metal rods form the three sides of an equilateral triangle. If the moment of inertia of the system of these three rods about an axis passing through the centroid of the triangle and perpendicular to the plane of the triangle is 'n' times the moment of inertia of one rod separately about an axis passing through the centre of the rod and perpendicular to its length, the value of 'n' is
View Solution
