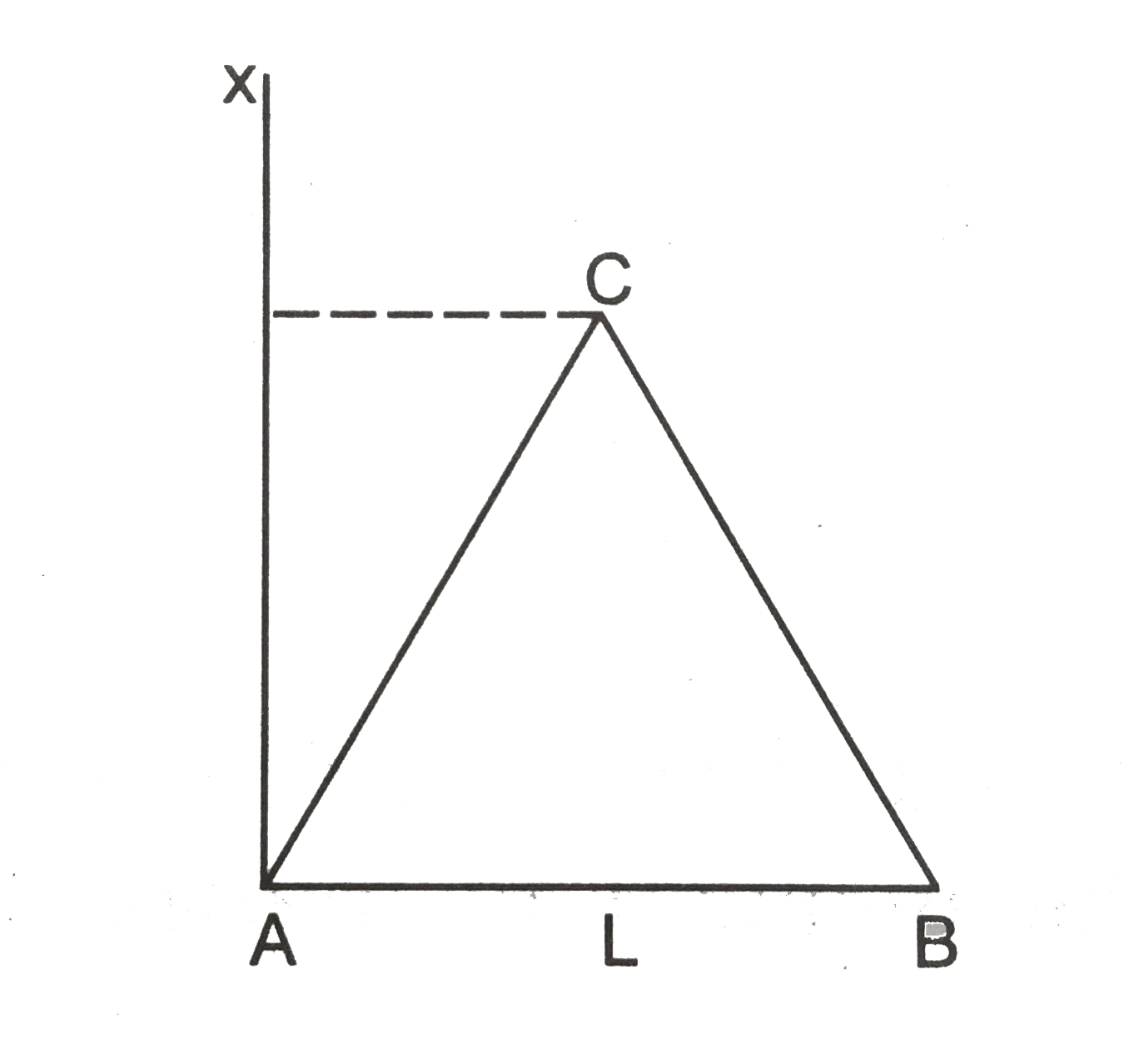
Three particles each of mass m gram are situated at the vertices of an equilateral triangle ABC of side L cm as shown in the figure.
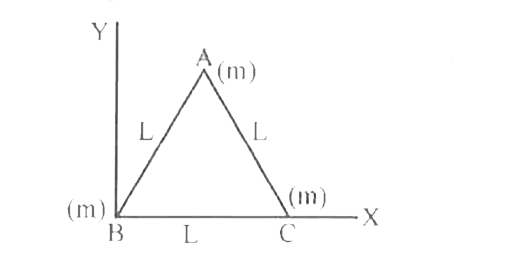
The moment of inertia of the system about a line BY perpendicular to BC and in the plane ABC is
32mL2gram - cm2
32mL2gram - cm2
54mL2gram - cm2
2 mL2gram - cm2
The correct Answer is:C
IB=mB(0)+mC(L2)+mA(BD)2
=mL2+m(L2)2=54mL2
Topper's Solved these Questions
Similar Questions
Three particles, each of mass m grams situated at the vertices of an equilateral triangle AbC of side I cm (as shown in the figure). The moment of inertia of the system about a line AX perpendicular to AB and in the plane of ABC, in gram-cm^2 units will be.
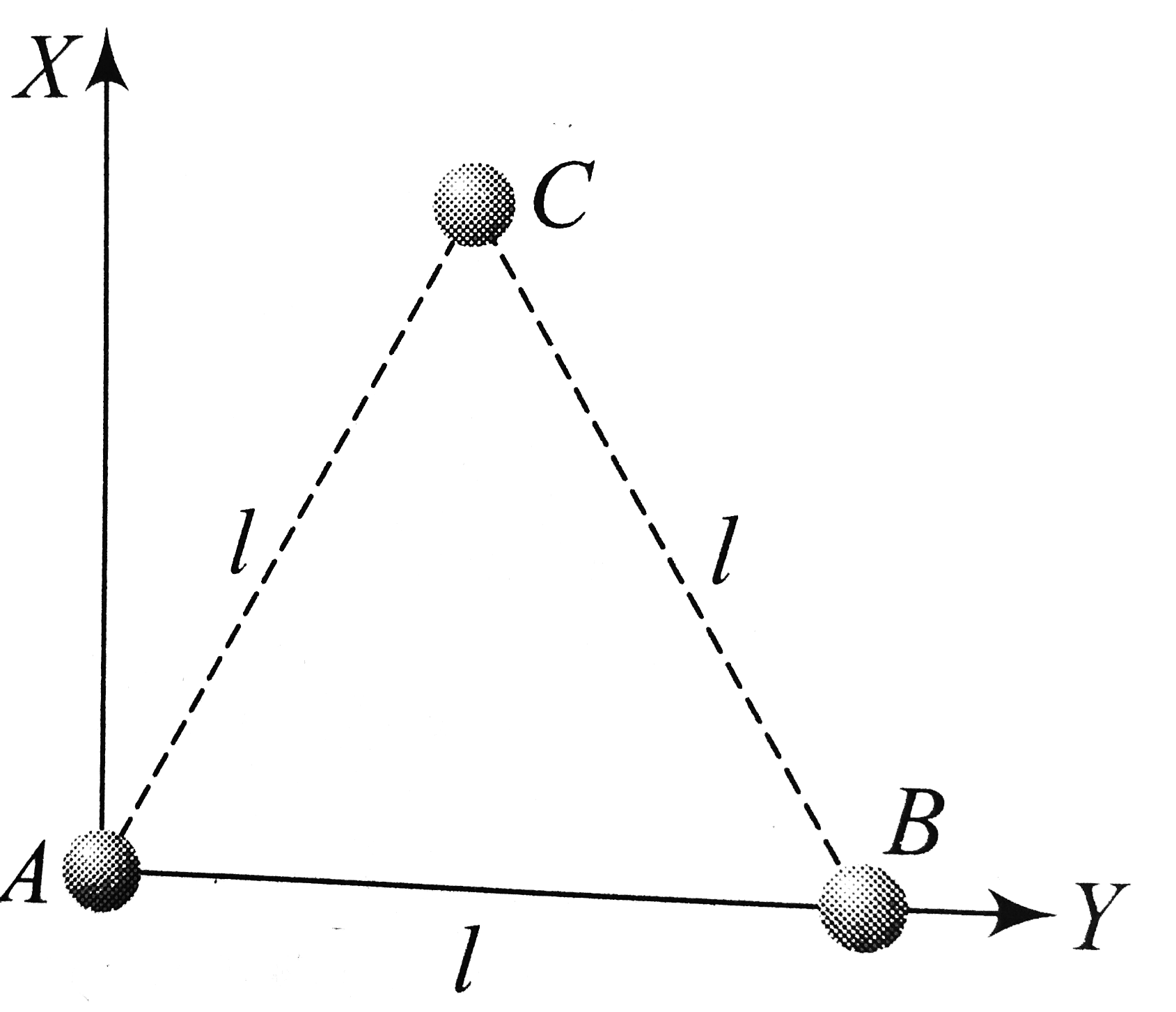 .
.
View SolutionThree particles, each of mass m are situated at the vertices of an equilateral triangle ABC of side l (as shown in the figure).
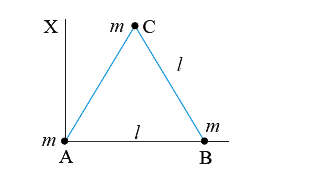
The moment of inertia of the system about a line AX perpendicular to AB and in the plane of ABC, will be:
View Solution
Knowledge Check
Three particles, each of mass m grams situated at the vertices of an equilateral triangle AbC of side I cm (as shown in the figure). The moment of inertia of the system about a line AX perpendicular to AB and in the plane of ABC, in gram-cm^2 units will be.
 .A(3/4)ml2B2ml2C(5/4)ml2D(3/2)ml2
.A(3/4)ml2B2ml2C(5/4)ml2D(3/2)ml2Three particles of equal mass 'm' are situated at the vertices of an equilateral triangle of side L. The work done in increasing the side of the triangle to 2L is
A2G2m2LBGm22LC3Gm22LD3Gm2LThree particles each of 'm' are kept at the three vertices of an equilateral triangle of side 'a' . Moment of inertia of the system about an axis passing through the centroid and perpendicular to its plane is
A3ma2Bma2Cma2/3D2/3ma2
Three particles, each of mass m are situated at the vertices of an equilateral triangle ABC of side l (as shown in the figure).

The moment of inertia of the system about a line AX perpendicular to AB and in the plane of ABC, will be:
View SolutionThree particles, each of mass m are situated at the vertices of an equilateral triangle ABC of side L as shown in the figure. Find the moment of inertia of the system about the line AX perpendicular to AB in the plane of ABC
View SolutionThree particles, each of mass m are situated at the vertices of an equilateral triangle ABC of side L figure. Find thee moment of inertia of the system about the line AX perpendicular to AB in the plane of ABC

View SolutionThree particles each of mass 12 g are located at the vertices of an equilateral triangle of side 10 cm. Calculate the moment of inertia of the system about an axis passing through the centroid and perpendicular to the plane of the triangle?
View SolutionThree particles of equal mass 'm' are situated at the vertices of an equilateral triangle of side L. The work done in increasing the side of the triangle to 2L is
View Solution
