Three particles of equal mass 'm' are situated at the vertices of an equilateral triangle of side L. The work done in increasing the side of the triangle to 2L is
5.0×10−12J
2.25×10−10J
4.0×x10−11J
6.0×10−15J
The correct Answer is:A
To find the work done in increasing the side of an equilateral triangle formed by three particles of equal mass 'm' from length L to 2L, we need to calculate the change in gravitational potential energy of the system.
1. Understanding the System:
We have three particles of mass m at the vertices of an equilateral triangle with side length L. The gravitational potential energy (U) between any two masses is given by the formula:
\(
U = -\frac{G m_1 m_2}{r}
\)
where \( G \) is the gravitational constant, \( m_1 \) and \( m_2 \) are the masses, and \( r \) is the distance between them.
2. Calculating Initial Potential Energy (U_initial):
For three particles, the potential energy due to the pairwise interactions is:
\(
U_{\text{initial}} = U_{12} + U_{13} + U_{23}
\)
Each pair has a distance of L, so:
\(
U_{12} = -\frac{G m m}{L}, \quad U_{13} = -\frac{G m m}{L}, \quad U_{23} = -\frac{G m m}{L}
\)
Therefore, the total initial potential energy is:
\(
U_{\text{initial}} = 3 \left(-\frac{G m^2}{L}\right) = -\frac{3G m^2}{L}
\)
3. Calculating Final Potential Energy (U_final):
When the side length is increased to 2L, the potential energy for each pair becomes:
\(
U_{12} = -\frac{G m m}{2L}, \quad U_{13} = -\frac{G m m}{2L}, \quad U_{23} = -\frac{G m m}{2L}
\)
Thus, the total final potential energy is:
\(
U_{\text{final}} = 3 \left(-\frac{G m^2}{2L}\right) = -\frac{3G m^2}{2L}
\)
4. Calculating the Work Done (W):
The work done in changing the configuration of the system is equal to the change in potential energy:
\(
W = U_{\text{final}} - U_{\text{initial}}
\)
Substituting the values we calculated:
\(
W = \left(-\frac{3G m^2}{2L}\right) - \left(-\frac{3G m^2}{L}\right)
\)
Simplifying this gives:
\(
W = -\frac{3G m^2}{2L} + \frac{3G m^2}{L} = \frac{3G m^2}{L} - \frac{3G m^2}{2L} = \frac{3G m^2}{2L}
\)
5. Final Result:
Therefore, the work done in increasing the side of the triangle from L to 2L is:
\(
W = \frac{3G m^2}{2L}
\)
We have three particles of mass m at the vertices of an equilateral triangle with side length L. The gravitational potential energy (U) between any two masses is given by the formula:
\(
U = -\frac{G m_1 m_2}{r}
\)
where \( G \) is the gravitational constant, \( m_1 \) and \( m_2 \) are the masses, and \( r \) is the distance between them.
For three particles, the potential energy due to the pairwise interactions is:
\(
U_{\text{initial}} = U_{12} + U_{13} + U_{23}
\)
Each pair has a distance of L, so:
\(
U_{12} = -\frac{G m m}{L}, \quad U_{13} = -\frac{G m m}{L}, \quad U_{23} = -\frac{G m m}{L}
\)
Therefore, the total initial potential energy is:
\(
U_{\text{initial}} = 3 \left(-\frac{G m^2}{L}\right) = -\frac{3G m^2}{L}
\)
When the side length is increased to 2L, the potential energy for each pair becomes:
\(
U_{12} = -\frac{G m m}{2L}, \quad U_{13} = -\frac{G m m}{2L}, \quad U_{23} = -\frac{G m m}{2L}
\)
Thus, the total final potential energy is:
\(
U_{\text{final}} = 3 \left(-\frac{G m^2}{2L}\right) = -\frac{3G m^2}{2L}
\)
The work done in changing the configuration of the system is equal to the change in potential energy:
\(
W = U_{\text{final}} - U_{\text{initial}}
\)
Substituting the values we calculated:
\(
W = \left(-\frac{3G m^2}{2L}\right) - \left(-\frac{3G m^2}{L}\right)
\)
Simplifying this gives:
\(
W = -\frac{3G m^2}{2L} + \frac{3G m^2}{L} = \frac{3G m^2}{L} - \frac{3G m^2}{2L} = \frac{3G m^2}{2L}
\)
Therefore, the work done in increasing the side of the triangle from L to 2L is:
\(
W = \frac{3G m^2}{2L}
\)
Topper's Solved these Questions
Similar Questions
Three particles, each of mass m are situated at the vertices of an equilateral triangle ABC of side L as shown in the figure. Find the moment of inertia of the system about the line AX perpendicular to AB in the plane of ABC

View SolutionThree particles each of mass m are kept at vertices of an equilateral triangle of side L. The gravitational field at centre due to these particle is
View SolutionThree particles, each of mass m are situated at the vertices of an equilateral triangle ABC of side l (as shown in the figure).
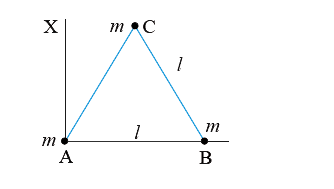
The moment of inertia of the system about a line AX perpendicular to AB and in the plane of ABC, will be:
View SolutionFind the coordinates of the vertices of an equilateral triangle of side 2a as shown in Figure.
View SolutionThree particles, each of mass m are fixed at the vertices of an equilateral triangle of side length a. The only forces acting on the particles are their mutual gravitational forces. Then answer the following questions.
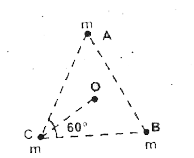
Force acting on particle C, due to particle A and B
View SolutionThree particles, each of mass m are fixed at the vertices of an equilateral triangle of side length a. The only forces acting on the particles are their mutual gravitational forces. Then answer the following questions.

The gravitational potential at O is
View SolutionThree particles, each of mass m grams situated at the vertices of an equilateral triangle AbC of side I cm (as shown in the figure). The moment of inertia of the system about a line AX perpendicular to AB and in the plane of ABC, in gram-cm^2 units will be.
 .
.
View SolutionThree particle each of mass m are placed at the corners of equilateral triangle of side l

Which of the following is/are correct ?
View SolutionThree particle of mass m each are placed at the three corners of an equilateral triangle of side a. Find the work which should be done on this system to increase the sides of the triangle to 2a.
View SolutionThree particle of mass m each are placed at the three corners of an equilateral triangle of side a. Find the work which should be done on this system to increase the sides of the triangle to 2a.
View Solution
