Three particles, each of the mass are situated at the vertices of an equilateral triangle of side . The only forces acting on the particles are their mutual gravitational forces. It is desired that each particle moves in a circle while maintaining the original mutual separation . Find the initial velocity that should be given to each particle and also the time period of the circular motion.
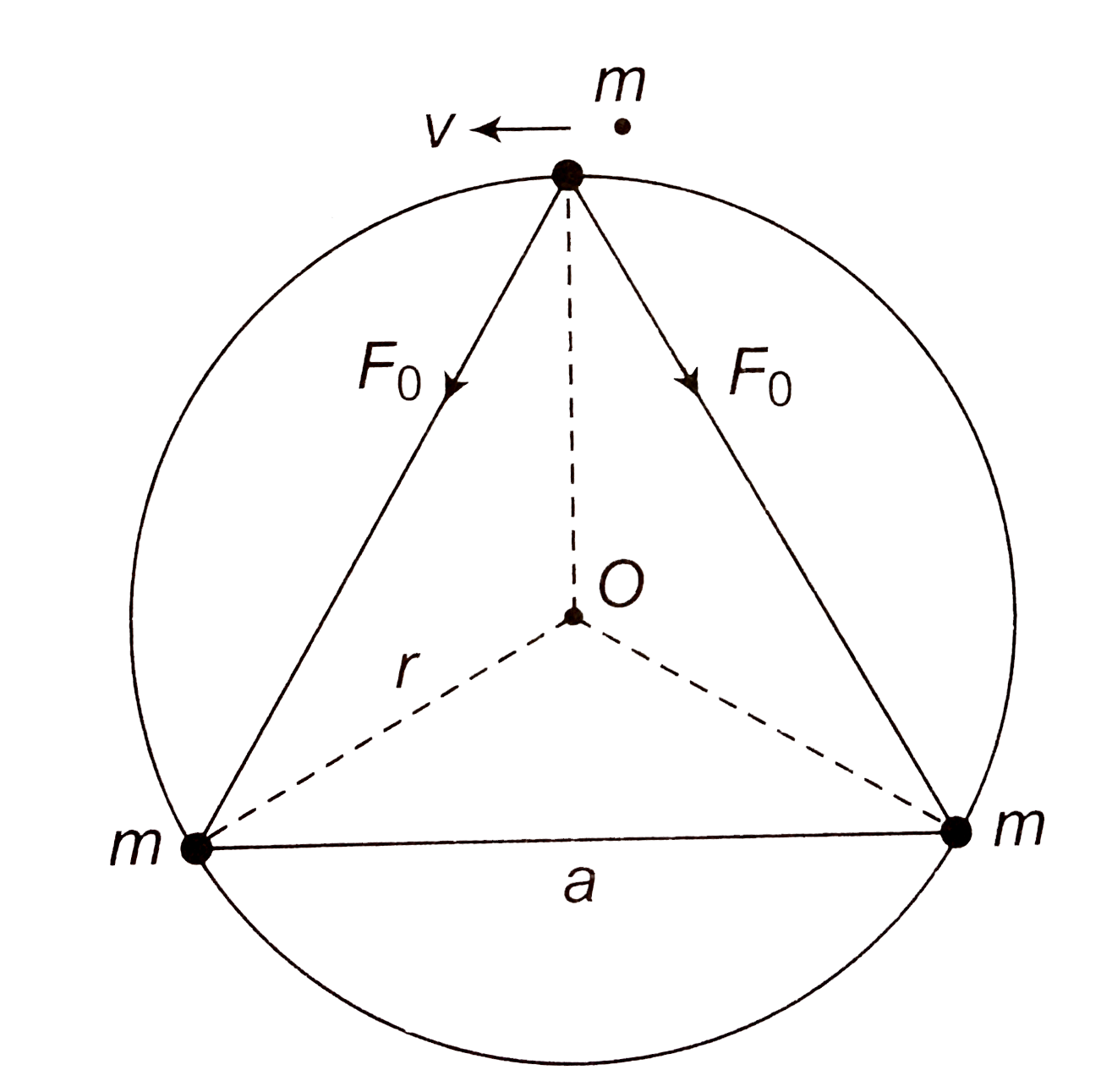
The resultant gravitational force acting on the particle
To move in circle, necesary centripetal force is provided by gravitational force
Time period of circular motion
Topper's Solved these Questions
Similar Questions
Three parties, each of mass m, are situated at the vertices of an equilateral triangle of side length a . The only forces acting on the pariclaes are th eir mutual gravitational forces. It is desired that each particles moves ina a circle while maintaining the original mutual separation a. Find the initial velocity that should be given to each particle and also the time period of teh circular motion.
View SolutionThree particles, each of mass m, are situated at the situated at the vertices of an equilateral triangle of side 'a'. The only forces acting on the particles are their mutual gravitational forces. It is intended that each particle moves along a circle while maintaining their original separation 'a'. Determine the initial velocity that should be given to each particle and the time period of the circular motion. The resultant force on particle at A due to other two particles is
View Solution
Knowledge Check
- Question 1 - Select One
Three particles each of mass m are kept at vertices of an equilateral triangle of side L. The gravitational field at centre due to these particle is
AzeroB3GML2C9GML2D12GM√3L2 - Question 2 - Select One
Three particles each of mass m are kept at the vertices of an euilateral triangle of side L. The gravitational field at the centre due to these particle is
AzeroB3GML2C9GML2D2GML2 - Question 3 - Select One
Three particles of equal mass 'm' are situated at the vertices of an equilateral triangle of side L. The work done in increasing the side of the triangle to 2L is
A2G2m2LBGm22LC3Gm22LD3Gm2L
Three particles, each of mass m, are situated at the vertices of equilateral triangle of side length a. The only forces. It is desired that each particle moves in a circle while maintaining the original mutual speration a. Find the intial velocity that should be given to each particle and also the time period of the circular motion.
View SolutionThree particles, each of mass m are fixed at the vertices of an equilateral triangle of side length a. The only forces acting on the particles are their mutual gravitational forces. Then answer the following questions.

The gravitational potential at O isView SolutionThree particles, each of mass m are fixed at the vertices of an equilateral triangle of side length a. The only forces acting on the particles are their mutual gravitational forces. Then answer the following questions.
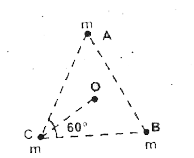
Force acting on particle C, due to particle A and BView SolutionThree particles each of mass m are palced at the corners of an equilateral triangle of side b. The gravitational potential energy of the system of particle is
View SolutionThree particles each of mass m are kept at the vertices of an euilateral triangle of side L. The gravitational field at the centre due to these particle is
View Solution

