Three particles of masses 1kg,32kg,and2kg are located at the vertices of an equilateral triangle of side a. The x,y coordinates of the centre of mass are.
(5a9,2a3√3)
(2a33,5a9)
(5a9,2a√3)
(2a√3,5a9)
The correct Answer is:A
To find the coordinates of the center of mass of the three particles located at the vertices of an equilateral triangle, we can follow these steps:
1. Identify the Masses and Their Positions:
- Let the masses be:
- m1=1kg at vertex A (0, 0)
- m2=32kg at vertex B (a, 0)
- m3=2kg at vertex C (a/2, √32a)
2. Calculate the Total Mass:
M=m1+m2+m3=1+32+2=72kg
3. Calculate the x-coordinate of the Center of Mass:
The formula for the x-coordinate of the center of mass is:
xcm=1M∑mixi
Substituting the values:
xcm=172(1⋅0+32⋅a+2⋅a2)
Simplifying:
xcm=27(0+3a2+a)=27(3a2+2a2)=27(5a2)=5a7
4. Calculate the y-coordinate of the Center of Mass:
The formula for the y-coordinate of the center of mass is:
ycm=1M∑miyi
Substituting the values:
ycm=172(1⋅0+32⋅0+2⋅√32a)
Simplifying:
ycm=27(0+0+√3a)=2√3a7
5. Final Result:
The coordinates of the center of mass are:
(5a7,2√3a7)
- Let the masses be:
- m1=1kg at vertex A (0, 0)
- m2=32kg at vertex B (a, 0)
- m3=2kg at vertex C (a/2, √32a)
M=m1+m2+m3=1+32+2=72kg
The formula for the x-coordinate of the center of mass is:
xcm=1M∑mixi
Substituting the values:
xcm=172(1⋅0+32⋅a+2⋅a2)
Simplifying:
xcm=27(0+3a2+a)=27(3a2+2a2)=27(5a2)=5a7
The formula for the y-coordinate of the center of mass is:
ycm=1M∑miyi
Substituting the values:
ycm=172(1⋅0+32⋅0+2⋅√32a)
Simplifying:
ycm=27(0+0+√3a)=2√3a7
The coordinates of the center of mass are:
(5a7,2√3a7)
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Displacement , Velocity And Acceleration Of Centre Of Mass30videos
ROTATIONAL DYNAMICS
- BOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Moment Of Inertia39videos
ROTATIONAL DYNAMICS
- BOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Chapter Test29videos
PROPERTIES OF MATTER
- BOOK - A2ZCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Chapter Test30videos
THERMAL PROPERTIES OF MATTER
Similar Questions
Three masses 2 kg , 3kg and 4kg are lying at the corners of an equilateral triangle of side I. The X coordinate of center of mass is
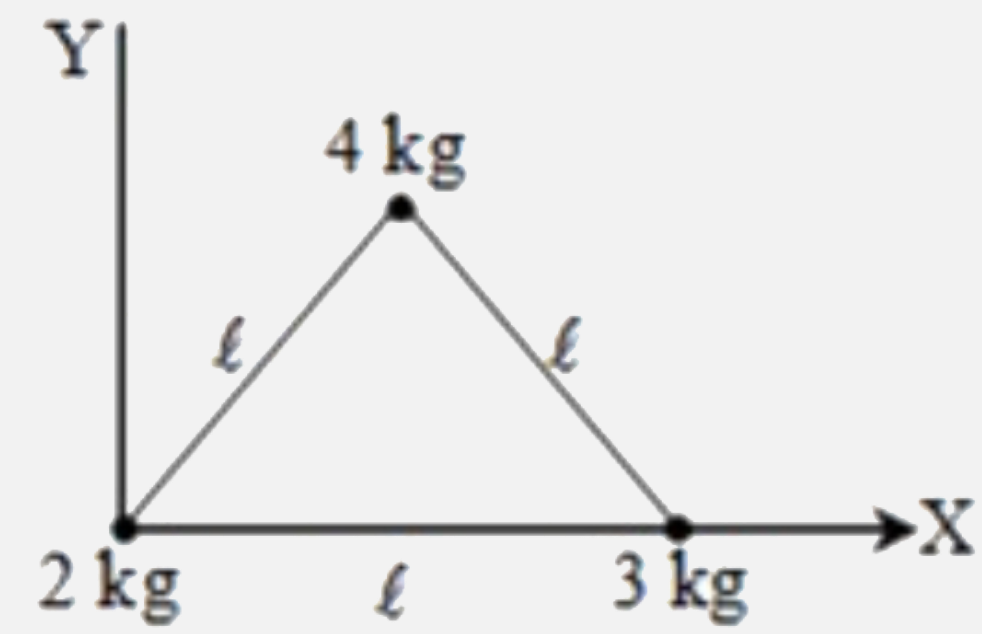 View Solution
View SolutionIf three point masses m1,m2andm3 are situated at the vertices of an equilateral triangle of side a, then what will be the co-ordinates of the centre of mass of this system ?
View Solution
Knowledge Check
- Question 1 - Select One
Three particles of masses 1kg,32kg,and2kg are located at the vertices of an equilateral triangle of side a. The x,y coordinates of the centre of mass are.
A(5a9,2a3√3)B(2a33,5a9)C(5a9,2a√3)D(2a√3,5a9) - Question 2 - Select One
Three particles of masses m1=1kg,m2=2kg and m3=3kg are kept at the vertices of an equilateral triangle of side 1 m. What is the x co-ordinate of its centre of mass?
A34mB45mC67mD712m - Question 3 - Select One
The PE of three objects of masses 1kg,2kg and 3kg placed at the three vertices of an equilateral triangle of side 20cm is
A25GB35GC45GD55G
Three masses 3,4 and 5 kg are located at the corners of an equilateral triangle of side 1m. Locate to centre of mass of the system.
View SolutionThe coordinates of a triangle ABC are A(1,2), B(4,6) and C(−3,−2). Three particles of masses 1kg, 2kg and mkg are placed the vertices of the triangle. If the coordinate of the centre of mass are (35,2), calculate the mass m.
View SolutionThree particles of msses 1.0 kg 2.0 kg and 3.0 kg are placed at the corners A,B and C respectively of an equilateral triangle ABC of edge 1m. Locate the centre ofmass of the system.
View SolutionThree particles of massses 50 g, 100 g and 150 g are placed at the vertices of an equilateral triangle of side 1m ( as shown in the figure ) . The ( x, y) coordinates of the centre of mass will be :
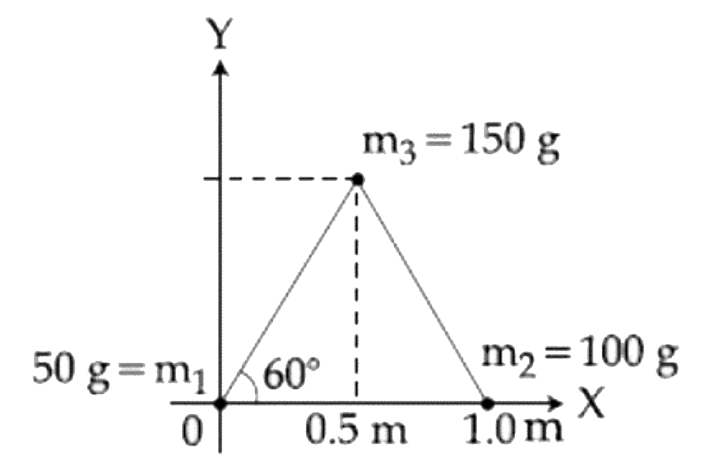 View Solution
View SolutionThree particles of masses 1 kg, 2 kg and 3 kg are situated at the corners of an equilateral triangle of side b in the x-y plane with mass 1 kg at the origin and 2 kg on the x-axis. The coordinates of the centre of mass are
View Solution

