The coordinates of a triangle ABC are A(1,2), B(4,6) and C(−3,−2). Three particles of masses 1kg, 2kg and mkg are placed the vertices of the triangle. If the coordinate of the centre of mass are (35,2), calculate the mass m.
To find the mass m of the third particle placed at vertex C(−3,−2) of triangle ABC, we can use the formula for the center of mass (COM) of a system of particles. The coordinates of the center of mass (xcm,ycm) for three particles with masses m1,m2,m3 located at coordinates (x1,y1),(x2,y2),(x3,y3) are given by:
xcm=m1x1+m2x2+m3x3m1+m2+m3
ycm=m1y1+m2y2+m3y3m1+m2+m3
Step 1: Identify the given values
- Masses:
- m1=1kg at A(1,2)
- m2=2kg at B(4,6)
- m3=mkg at C(−3,−2)
- Coordinates of the center of mass:
- xcm=35
- ycm=2
Step 2: Set up the equations for the center of mass
Using the formula for xcm:
1⋅1+2⋅4+m⋅(−3)1+2+m=35
This simplifies to:
1+8−3m3+m=35
Using the formula for ycm:
1⋅2+2⋅6+m⋅(−2)1+2+m=2
This simplifies to:
2+12−2m3+m=2
Step 3: Solve the equations
For the x-coordinate:
Cross-multiplying gives:
5(1+8−3m)=3(3+m)
Expanding both sides:
5(9−3m)=9+3m
45−15m=9+3m
Rearranging gives:
45−9=15m+3m
36=18m
m=2
For the y-coordinate:
Cross-multiplying gives:
2(3+m)=2+12−2m
Expanding both sides:
6+2m=14−2m
Rearranging gives:
6+2m+2m=14
6+4m=14
4m=8
m=2
Conclusion
The mass m of the third particle at vertex C is 2kg.
- Masses:
- m1=1kg at A(1,2)
- m2=2kg at B(4,6)
- m3=mkg at C(−3,−2)
- xcm=35
- ycm=2
Using the formula for xcm:
The mass m of the third particle at vertex C is 2kg.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Illustration4videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - AAKASH INSTITUTECHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - A) Objective Type Questions (One option is correct)62videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - AAKASH INSTITUTECHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))5videos
SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITS
- BOOK - AAKASH INSTITUTECHAPTER - TEST 1EXERCISE - EXERCISE9videos
TEST 1
Similar Questions
Knowledge Check
- Question 1 - Select One
Three particles of masses 1kg,32kg,and2kg are located at the vertices of an equilateral triangle of side a. The x,y coordinates of the centre of mass are.
A(5a9,2a3√3)B(2a33,5a9)C(5a9,2a√3)D(2a√3,5a9) - Question 2 - Select One
Three particles of masses m1=1kg,m2=2kg and m3=3kg are kept at the vertices of an equilateral triangle of side 1 m. What is the x co-ordinate of its centre of mass?
A34mB45mC67mD712m - Question 3 - Select One
Four particles of masses 1kg, 2kg, 3kg and 4kg are placed at the four vertices A, B, C and D of a square of side 1m. Find the position of centre of mass of the particles.
A(0.5,0.3)B(0.4,0.3)C(0.5,0.8)D(0.7,0.3)
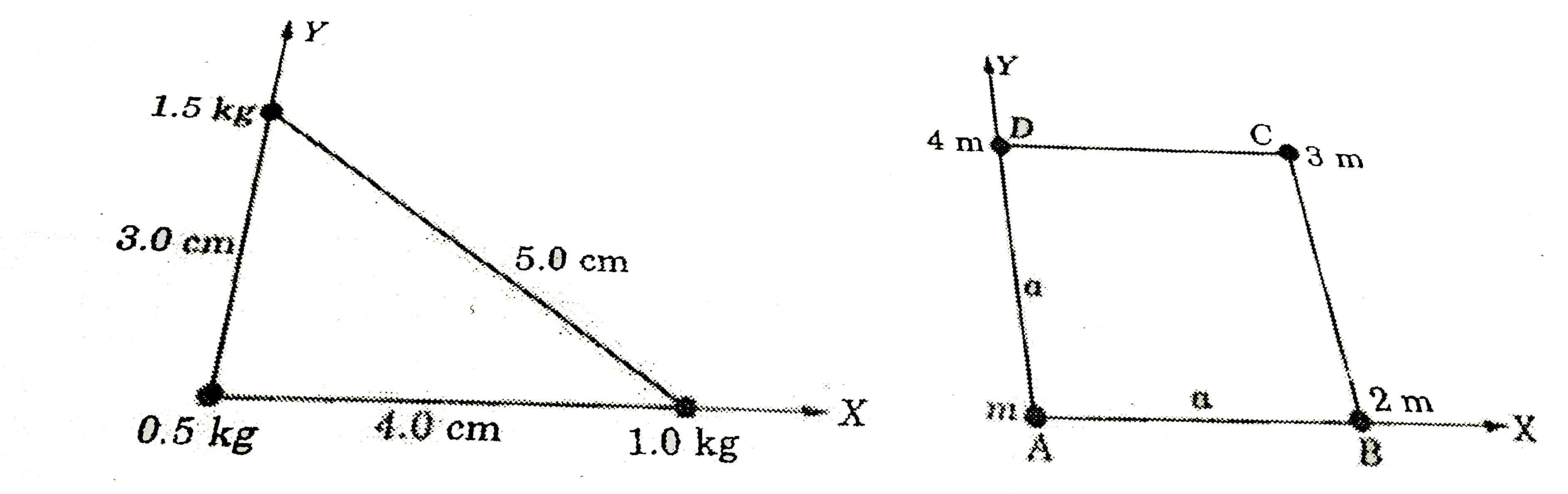
Three particles of masses 0.50 kg, 1.0 kg and are placed at the corners of a right angle triangle, as shown in fig. Locate the centre of mass of the system.
 View Solution
View SolutionThree masses 3,4 and 5 kg are located at the corners of an equilateral triangle of side 1m. Locate to centre of mass of the system.
View SolutionTwo bodies of masses 1 kg and 2 kg are located at (1,2) and (-1,3), respectively. Calculate the coordinates of center of mass.
View SolutionThree particles of masses 1kg, 2kg and 3kg are placed at the corners A, B and C respectively of an equilateral triangle ABC of edge 1m. Find the distance of their centre of mass from A.
View SolutionFind the PE of three objects of masses 1kg,2kg and 3kg placed at the three vertices of an equilateral triangle of side 50cm ?
View Solution