Three point charges q are placed at three vertices of an equilateral triangle of side a. Find magnitude of electric force on any charge due to the other two.
(√34πε0)(qa)2
(√24πε0)(qa)2
(√34πε0)(q2a)2
(√24πε0)(2qa)2
The correct Answer is:A
To find the magnitude of the electric force on any charge due to the other two charges placed at the vertices of an equilateral triangle, we can follow these steps:
Step 1: Understand the Configuration
Consider three point charges, each with charge q, placed at the vertices A, B, and C of an equilateral triangle with side length a. We will calculate the net electric force acting on charge q at vertex A due to the other two charges at vertices B and C.
Step 2: Calculate the Force Between Charges
According to Coulomb's Law, the electric force F between two point charges is given by:
F=k|q1q2|r2
where:
- k is Coulomb's constant (k≈8.99×109N m2/C2),
- q1 and q2 are the magnitudes of the charges,
- r is the distance between the charges.
In our case, the distance r between any two charges is a. Therefore, the force between any two charges q at distance a is:
FAB=FAC=kq2a2
Step 3: Determine the Direction of Forces
Since we are assuming that all charges have the same sign, the forces will be repulsive. Thus:
- The force FAB acts on charge A due to charge B and points away from B towards A.
- The force FAC acts on charge A due to charge C and points away from C towards A.
Step 4: Resolve Forces into Components
To find the net force on charge A, we need to resolve the forces FAB and FAC into their components. The angle between the lines connecting A to B and A to C is 60∘.
The horizontal component (x-direction) and vertical component (y-direction) of the forces can be calculated as follows:
- The x-component of FAB:
FABx=FABcos(60∘)=FAB⋅12=12kq2a2
- The y-component of FAB:
FABy=FABsin(60∘)=FAB⋅√32=√32kq2a2
Similarly, for FAC:
- The x-component of FAC:
FACx=FACcos(60∘)=12kq2a2
- The y-component of FAC:
FACy=FACsin(60∘)=√32kq2a2
Step 5: Calculate the Net Force Components
Now, we can find the net force components acting on charge A:
- The total x-component:
FAx=FABx+FACx=12kq2a2+12kq2a2=kq2a2
- The total y-component:
FAy=FABy−FACy=√32kq2a2+√32kq2a2=√3kq2a2
Step 6: Calculate the Magnitude of the Net Force
The magnitude of the net force FA on charge A can be calculated using the Pythagorean theorem:
FA=√(FAx)2+(FAy)2
Substituting the values:
FA=√(kq2a2)2+(√3kq2a2)2
FA=√k2q4a4+3k2q4a4=√4k2q4a4=2kq2a2
Final Result
Thus, the magnitude of the electric force on any charge due to the other two charges is:
F=2kq2a2
Consider three point charges, each with charge q, placed at the vertices A, B, and C of an equilateral triangle with side length a. We will calculate the net electric force acting on charge q at vertex A due to the other two charges at vertices B and C.
According to Coulomb's Law, the electric force F between two point charges is given by:
F=k|q1q2|r2
where:
- k is Coulomb's constant (k≈8.99×109N m2/C2),
- q1 and q2 are the magnitudes of the charges,
- r is the distance between the charges.
FAB=FAC=kq2a2
Since we are assuming that all charges have the same sign, the forces will be repulsive. Thus:
- The force FAB acts on charge A due to charge B and points away from B towards A.
- The force FAC acts on charge A due to charge C and points away from C towards A.
To find the net force on charge A, we need to resolve the forces FAB and FAC into their components. The angle between the lines connecting A to B and A to C is 60∘.
- The x-component of FAB:
FABx=FABcos(60∘)=FAB⋅12=12kq2a2
- The y-component of FAB:
FABy=FABsin(60∘)=FAB⋅√32=√32kq2a2
- The x-component of FAC:
FACx=FACcos(60∘)=12kq2a2
- The y-component of FAC:
FACy=FACsin(60∘)=√32kq2a2
Now, we can find the net force components acting on charge A:
- The total x-component:
FAx=FABx+FACx=12kq2a2+12kq2a2=kq2a2
- The total y-component:
FAy=FABy−FACy=√32kq2a2+√32kq2a2=√3kq2a2
The magnitude of the net force FA on charge A can be calculated using the Pythagorean theorem:
FA=√(FAx)2+(FAy)2
Substituting the values:
FA=√(kq2a2)2+(√3kq2a2)2
FA=√k2q4a4+3k2q4a4=√4k2q4a4=2kq2a2
Thus, the magnitude of the electric force on any charge due to the other two charges is:
F=2kq2a2
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.3
5 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.4
4 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Exercise 24.1
4 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEYCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - All Questions
120 Videos
Similar Questions
Three points charges are placed at the corners of an equilateral triangle of side L as shown in the figure:
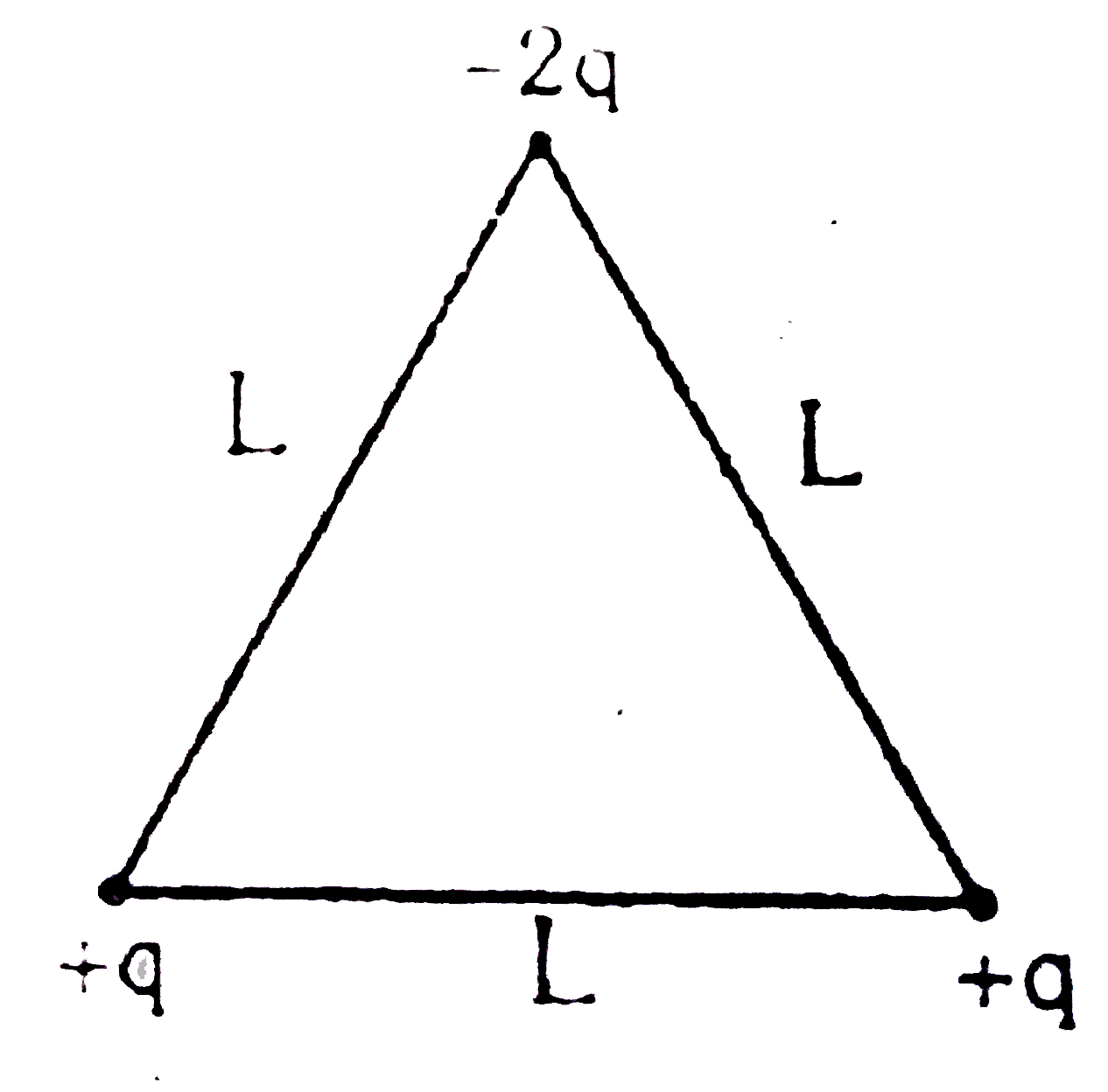
View Solution(i) Three equak charge q0 each are placed at three corners of an equilateral triangle of side 'a'. Find out dorce acting on one of the charge due to other two charges ?
(ii) In the above question, if one of the charge is replaced by negative charge then find out force acting on it due to other charges ?
(iii) Repeat the part (i) if magnitude of each charge is doubled and side of triangle is reduced to half.
View Solution
Knowledge Check
Equal charges q are placed at the vertices A and B of an equilatral triangle ABC of side a. The magnitude of electric field at the point C is
Aq4πε0a2B√2q4πε0a2C√3q4πε0a2Dq2πε0a2Three point charges + q each are kept at the vertices of an equilateral triangle of side l. Determine the magnitude and sign of charge to be kept at the centroid so that charges at the vertices remain in equillibrium.
AQ=2q√3BQ=q√2CQ=3q√3DQ=q√3Three charge −q,+q and −q are placed at the cornors of an equilateral triangle of side a The resultant electric froce an a charge +q placed at a the centroid O of the triangle is
A3q24πε0a2Bq24πε0a2Cq22πε0a2D3q22πε0a2
Three identical point charges Q are placed at the three corners of an equilateral triangle of side length a. Find the electric potential at points O and M due to the three charges.
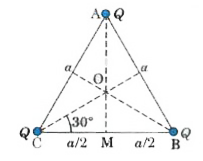
View SolutionConsider the charges q,q and -q placed at the vertices of an equilateral triangle of each side l. What is the force on each charge ?
View SolutionTwo charge +Q each are placed at the two verticles of an equilateral triangle of side a .The intensity of electric field at the third vertex is
View SolutionThree point masses 'm' each are placed at the three vertices of an equilateral traingle of side 'a'. Find net gravitational force on any point mass.
View SolutionElectric charges q,q,–2q are placed at the corners of an equilateral triangle ABC of side l. The magnitude of electric dipole moment of the system is
View Solution
