Question

Three point masses each of mass 'm' are kept at the corners of an equilateral triangle of side L. The system rotates about the centre of the triangle without any change in the separation of masses during the rotation. If T is the periodic time of rotatio then

Options

A. `T prop (1)/(L^(2))`
B. `T prop (1)/(m^(2))`
C. `T prop m^(1//2)`
D. `T prop L^(3//2)`

Answer

D

Explanation

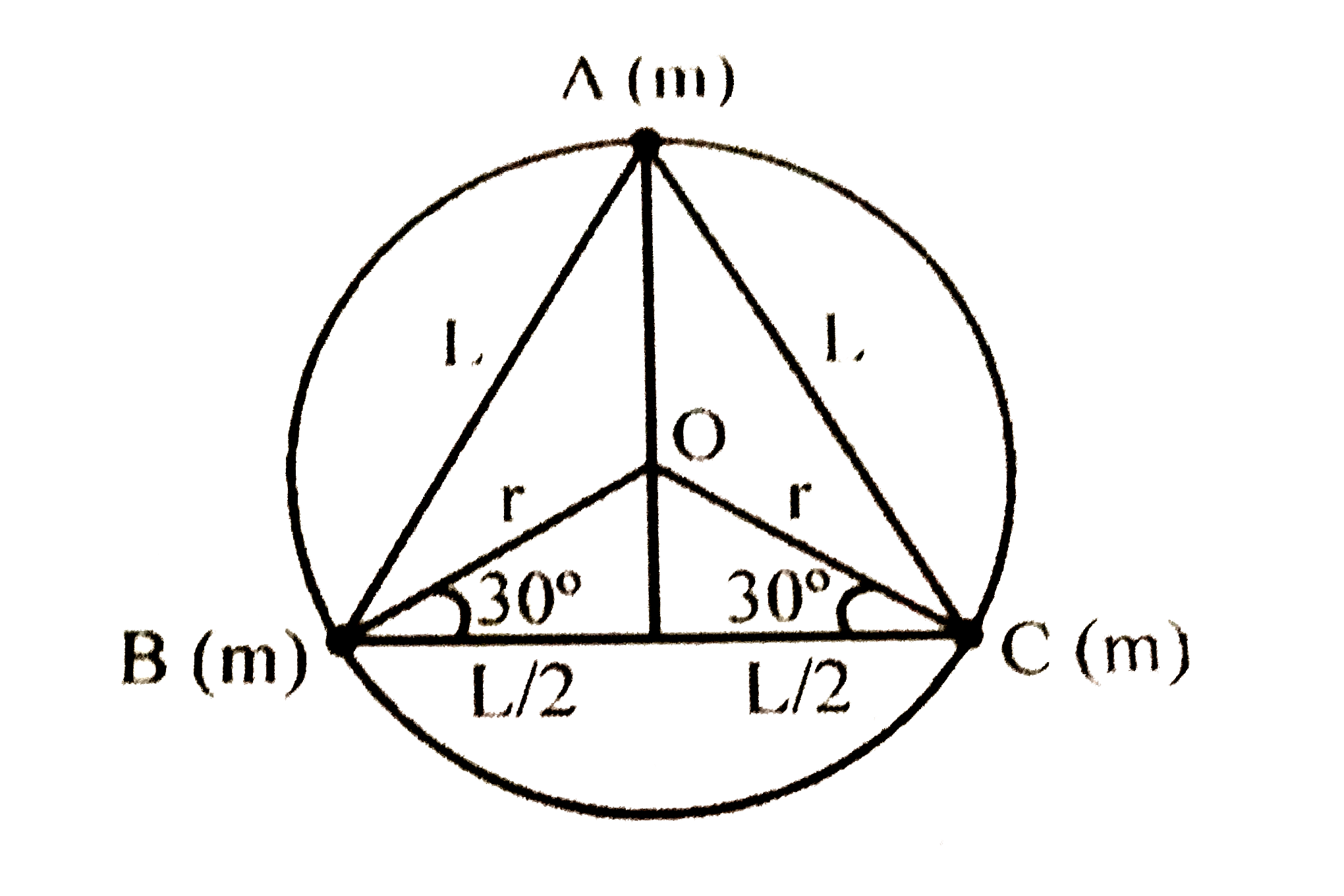
The masses are situated at the vertices of the `Delta ABC`.
From the figure,
`cos 30^(@)=(L//2)/(r ) therefore (sqrt(3))/(2)=(L)/(2r) therefore r = (L)/(sqrt(3)) " "` …..(1)
The gravitational force of attraction between any two masses provides the necessary C.P. force for the masses to revolve in a circle of radius r.
`therefore (Gmm)/(L^(2))=mr omega^(2) = mr.(4pi^(2))/(T^(2))`
`therefore T^(2)=(4pi^(2)mrL^(2))/(Gm^(2))=(4pi^(2)L^(3))/(sqrt(3)Gm)`
`therefore T = 2pi sqrt((L^(3))/(sqrt(3)Gm))" "` ...... Using (1)
But `2pi, sqrt(3)` and G are constant.
`therefore T prop L^(3//2)` and `T prop m^(-1//2)`
Thus `T prop L^(3//2)` is the correct option.