Three rods of same cross sectional area are made of same material and form the sides of a right-angled isosceles triangle PQR, right angled at Q. P and Q are maintained at temperature T and 2T, respectively. If the temperature of end R is T', then what is the ratio of T'/T. Assume that only heat conduction takes place.
To solve the problem, we need to analyze the heat conduction through the three rods forming the sides of a right-angled isosceles triangle PQR, where P and Q are at temperatures T and 2T, respectively, and we need to find the temperature T' at point R.
1. Understanding the Setup:
- We have three rods forming a right-angled isosceles triangle PQR, with P at temperature T and Q at temperature 2T.
- The rod PQ is vertical, QR is horizontal, and PR is the hypotenuse.
2. Heat Transfer in Steady State:
- In steady state, the heat flow from Q to P must equal the heat flow from P to R.
- We denote the thermal conductivity of the material as K and the cross-sectional area as A.
3. Heat Transfer from Q to P:
- The rate of heat transfer from Q to P can be expressed as:
QQP=KA(2T−T′)L
- Here, L is the length of the rod QP.
4. Heat Transfer from P to R:
- The rate of heat transfer from P to R (along the hypotenuse) is:
QPR=KA(T′−T)L√2
- The factor of √2 comes from the geometry of the triangle.
5. Setting the Heat Transfers Equal:
- Since the heat transfer rates are equal in steady state:
KA(2T−T′)L=KA(T′−T)L√2
- We can cancel K, A, and L from both sides:
2T−T′=1√2(T′−T)
6. Rearranging the Equation:
- Multiply both sides by √2 to eliminate the fraction:
√2(2T−T′)=T′−T
- Expanding gives:
2√2T−√2T′=T′−T
- Rearranging terms leads to:
2√2T+T=T′+√2T′
T′(1+√2)=(2√2+1)T
7. Solving for T':
- Now, we can solve for T′:
T′=(2√2+1)T(1+√2)
8. Finding the Ratio T'/T:
- The ratio T′T is:
T′T=2√2+11+√2
Final Answer:
The ratio T′T is 2√2+11+√2.
---
- We have three rods forming a right-angled isosceles triangle PQR, with P at temperature T and Q at temperature 2T.
- The rod PQ is vertical, QR is horizontal, and PR is the hypotenuse.
- In steady state, the heat flow from Q to P must equal the heat flow from P to R.
- We denote the thermal conductivity of the material as K and the cross-sectional area as A.
- The rate of heat transfer from Q to P can be expressed as:
QQP=KA(2T−T′)L
- Here, L is the length of the rod QP.
- The rate of heat transfer from P to R (along the hypotenuse) is:
QPR=KA(T′−T)L√2
- The factor of √2 comes from the geometry of the triangle.
- Since the heat transfer rates are equal in steady state:
KA(2T−T′)L=KA(T′−T)L√2
- We can cancel K, A, and L from both sides:
2T−T′=1√2(T′−T)
- Multiply both sides by √2 to eliminate the fraction:
√2(2T−T′)=T′−T
- Expanding gives:
2√2T−√2T′=T′−T
- Rearranging terms leads to:
2√2T+T=T′+√2T′
T′(1+√2)=(2√2+1)T
- Now, we can solve for T′:
T′=(2√2+1)T(1+√2)
- The ratio T′T is:
T′T=2√2+11+√2
The ratio T′T is 2√2+11+√2.
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - REVISION EXERCISE (VERY SHORT ANSWER QUESTION)
33 Videos
- THERMAL PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - REVISION EXERCISE (ADDITIONAL QUESTION)
3 Videos
- THERMAL PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - NCERT FILE (TEXTBOOK EXERCISE)
25 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Chapter Practice Test (for Board Examination)
16 Videos
- UNITS AND MEASUREMENTBOOK - MODERN PUBLICATIONCHAPTER - UNITS AND MEASUREMENTEXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
Four rods of identical cross-sectional area and made from the same metal form the sides of square. The temperature of two diagonally opposite points are T and√2T respectively in the steady state. Assuming that only heat conduction takes place, what will be the temperature difference between other two points
View SolutionThree rods of identical area of cross-section and made from the same metal from the sides of an isosceles triangle. ABC, right angled at B. The points A and B are maintained at temperatures T and √2T respectively. In the steady state the temperature of the point C is TC.
Assuming that only heat conduction takes place , TCT is equal to
View Solution
Knowledge Check
Three rods of identical cross-sectional area and made from the same metal form the sides of an isosceles triangle ABC right angled at B as shown in the figure. The points A and B are maintained at temperature T and (√2)T respectively in the steady state. Assuming that only heat conduction takes place, temperature of point C will be
 AT(√2)−1BT(√2)+1C3T(√2)+1DT(√3)(√2−1)
AT(√2)−1BT(√2)+1C3T(√2)+1DT(√3)(√2−1)Three rods of identical cross-sectional area and made from the same metal form the sides of an isosceles triangle ABC right angled at B as shown in the figure. The points A and B are maintained at temperature T and (√2)T respectively in the steady state. Assuming that only heat conduction takes place, temperature of point C will be
 AT√2+1BT√2−1C3T√2+1D√3T(√2+1)
AT√2+1BT√2−1C3T√2+1D√3T(√2+1)Three rods of identical cross-sectional area and made from the same metal form the sides of an insosceles triangle ABC right angled at B The pints A and B are maintained at temperatures T and √T respectively in the steady state Assuming that only heat conduction takes place, temperature of point C is .
 .A3T√2+1BT√2+1CT3(√2−1)DT√2−1
.A3T√2+1BT√2+1CT3(√2−1)DT√2−1
Three rods of identical cross-sectional area and made from the same metal form the sides of an equilateral triangle ABC The points A and B are maintained at temperature √3T and T respectively In the steady state, the temperature of the point C is TC Assuming that only heat conduction takes place, the value of TC/T is equal to .
View SolutionThree rods of identical cross-sectional area and made from the same metal, from the sides of an isosceles triangle ABC right angled at B, as shown in Fig .7(CF).23. The points A and B are maintained at temperature T and √2T respectively in the steady. Assuming that only heat conduction takes place, temperature of point C will be
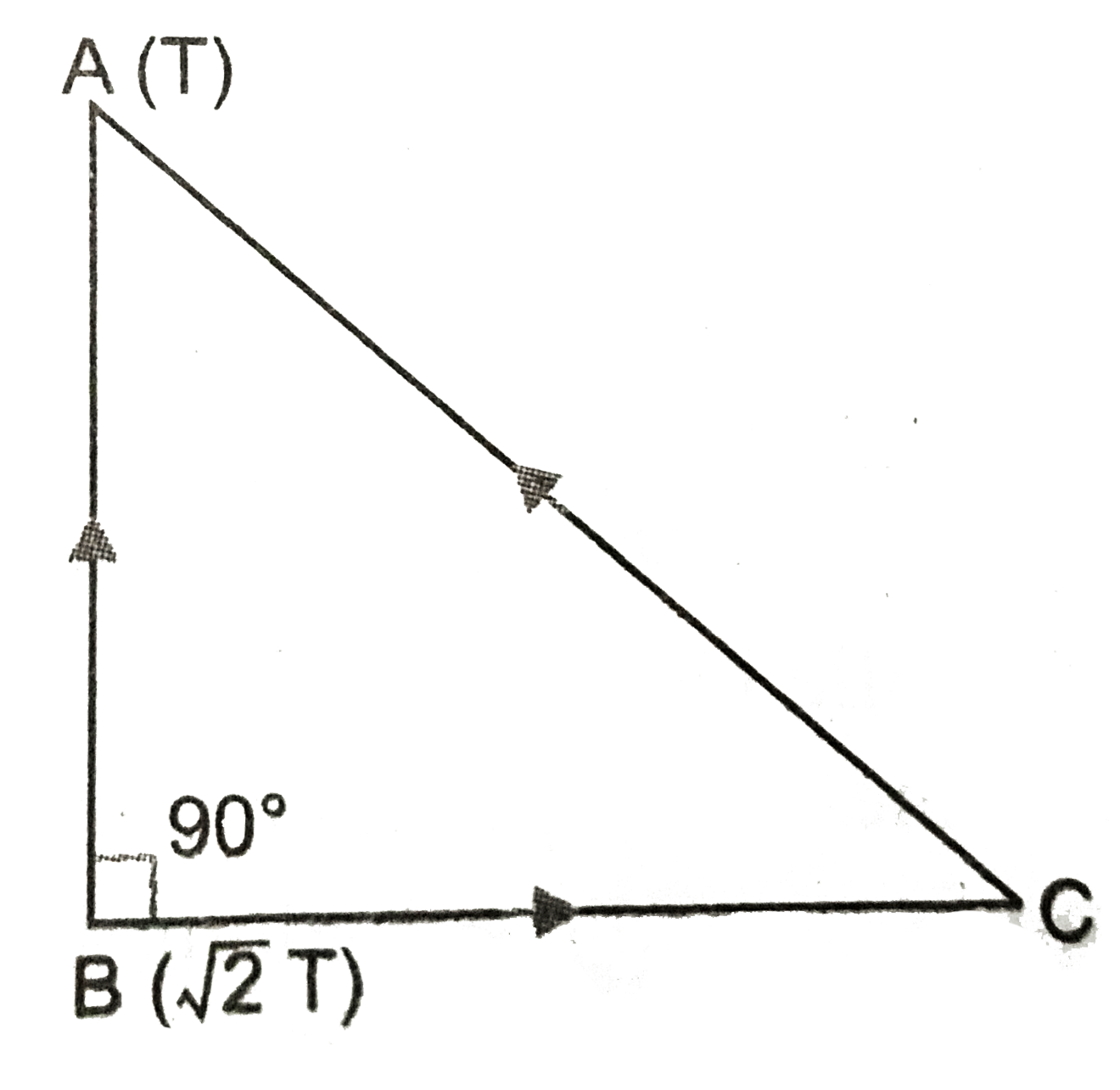
View Solution
Three rods of identical cross-sectional area and made from the same metal form the sides of an isosceles Delta ABC right angled at B. The points A and B are maintained at temperetures T and √2T, respectively in the steady state. Assuming that only heat conduction takes place, temperature of point C is
View SolutionThree very large plates of same area are kept parallel and close to each other. They are considered as ideal black surface and have very high thermal conductivity The first and third plates are maintained at temperatures 2T and 3T respectively Find the temperature of the middle (i.e second) plate under steady state .
View SolutionThe three rods of same meterial and crosssectional area from the sides of a triangle ABC The points A,B and C are maintained at temperature TT√2 and 3T(√2+1) respectively Assuming that only heat conducting takes place the system is in steady state, find the angle at B The temperature difference per unit length along SB and CA is equal
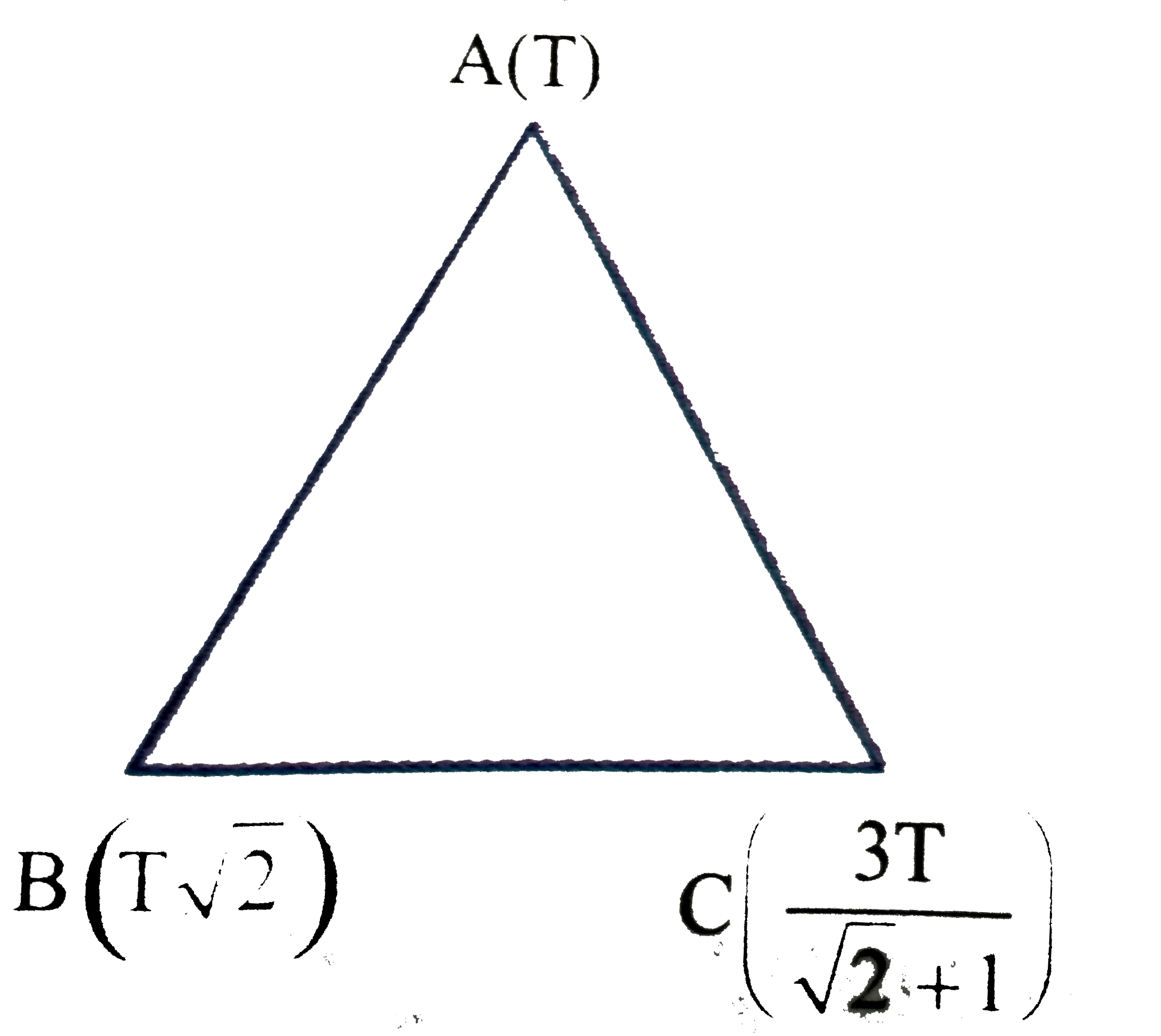 .
.
View Solution