A heater of resistance R maintains a room at T0∘C and is connected to a mains supply of V volt. The heat is transmitted through a glass window of area A and thickness d. If the thermal conductivity of the glass is K, find the expression for the outside temperature.
To solve the problem, we need to find the expression for the outside temperature T given the parameters of the heater and the glass window. Let's break down the solution step by step.
Step 1: Determine the Power of the Heater
The power P generated by the heater can be calculated using the formula for electrical power:
P=V2R
where V is the voltage of the mains supply and R is the resistance of the heater.
Step 2: Apply the Law of Thermal Conductivity
According to the law of thermal conductivity, the rate of heat transfer dQdt through the glass window can be expressed as:
dQdt=KA(T0−T)d
where:
- K is the thermal conductivity of the glass,
- A is the area of the glass window,
- T0 is the inside temperature (room temperature),
- T is the outside temperature,
- d is the thickness of the glass.
Step 3: Set the Heat Generated Equal to the Heat Lost
At thermal equilibrium, the heat generated by the heater equals the heat lost through the glass window:
V2R=KA(T0−T)d
Step 4: Rearrange the Equation to Solve for T
We can rearrange the equation to isolate T:
T0−T=V2dKAR
T=T0−V2dKAR
Final Expression for the Outside Temperature
Thus, the expression for the outside temperature T is:
T=T0−V2dKAR
The power P generated by the heater can be calculated using the formula for electrical power:
P=V2R
where V is the voltage of the mains supply and R is the resistance of the heater.
According to the law of thermal conductivity, the rate of heat transfer dQdt through the glass window can be expressed as:
dQdt=KA(T0−T)d
where:
- K is the thermal conductivity of the glass,
- A is the area of the glass window,
- T0 is the inside temperature (room temperature),
- T is the outside temperature,
- d is the thickness of the glass.
At thermal equilibrium, the heat generated by the heater equals the heat lost through the glass window:
V2R=KA(T0−T)d
We can rearrange the equation to isolate T:
T0−T=V2dKAR
T=T0−V2dKAR
Thus, the expression for the outside temperature T is:
T=T0−V2dKAR
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - REVISION EXERCISE (VERY SHORT ANSWER QUESTION)
33 Videos
- THERMAL PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - REVISION EXERCISE (ADDITIONAL QUESTION)
3 Videos
- THERMAL PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - NCERT FILE (TEXTBOOK EXERCISE)
25 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Chapter Practice Test (for Board Examination)
16 Videos
- UNITS AND MEASUREMENTBOOK - MODERN PUBLICATIONCHAPTER - UNITS AND MEASUREMENTEXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
A heater of resistance 20 Ω is used to heat a room at 10∘C and is connected to 220 V mains. The temperature is uniform inside the room and heat is transmitted outside the room through a glass window of area 1.2m2 and thickness 0.1 cm. If T∘C is the temperature outside and thermal conductivity of glass is0.2cals−1m−1∘C−1 , then find the value of 10T - 75 close to nearest integer.
View SolutionA room is to be maintained at a constant temperature of 30∘C and is heated by a heater of resistance 10Ω connected to 210 V mains supply. Heat is transmitted outside through a window of thickness 0.3 cm and area 2m2 What will be temperature outside the window?
Thermal conductivity of glass =0.3cals−1m−1∘C−1
View Solution
Knowledge Check
A room at 20∘C is heated by a heater of resistence 20 ohm connected to 200 VV mains. The temperature is uniform throughout the room and the heati s transmitted through a glass window of area 1m2 and thickness 0.2 cm. Calculate the temperature outside. Thermal conductivity of glass is 0.2cal/mC∘ s and mechanical equivalent of heat is 4.2J/cal.
A13.69∘CB15.24∘CC17.85∘CD19.96∘CA room at 20∘C is heated by a heater of resistence 20 ohm connected to 200 VV mains. The temperature is uniform throughout the room and the heati s transmitted through a glass window of area 1m2 and thickness 0.2 cm. Calculate the temperature outside. Thermal conductivity of glass is 0.2cal/mC∘ s and mechanical equivalent of heat is 4.2J/cal.
A13.69∘CB15.24∘CC17.85∘CD19.96∘CA heating element has a resistance of 100 Ω at room temperature. When it is connected to a supply of 220 V, a steady current of 2A passes in it and temperature is 500∘C more than room temperature. What is the temperature coefficient of resistance of the heating element ?
A2×10−4.∘C−1B0.5×10−4.∘C−1C1×10−4.∘C−1D5×10−4.∘C−1
Steam at 373 K is passed through a tube of radius 10cm and length10cm and length 2m. The thickness of the tube is 5mm and thermal conductivity of the material is390Wm−1K−1, calculate the heat lost per second. The outside temperature is 0∘C.
View SolutionA heat source at T = 103 K is connected to another heat reservoir at T = 102 K by a copper slab which is 1 m thick. Given that the thermal conductivity of copper is 0.1 WK−1m−1, the energy flux through it in steady state is :
View SolutionThe temperature of the filament of 100−watt lamp is 4000∘C in the steady state and the radius of the glass bulb is 4 cm and the thickness of the wall is 0.4mm. Assuming that there is no convection, calculate the thermal conductivity of glass. The temperature of the outside air is 27∘C.
View Solution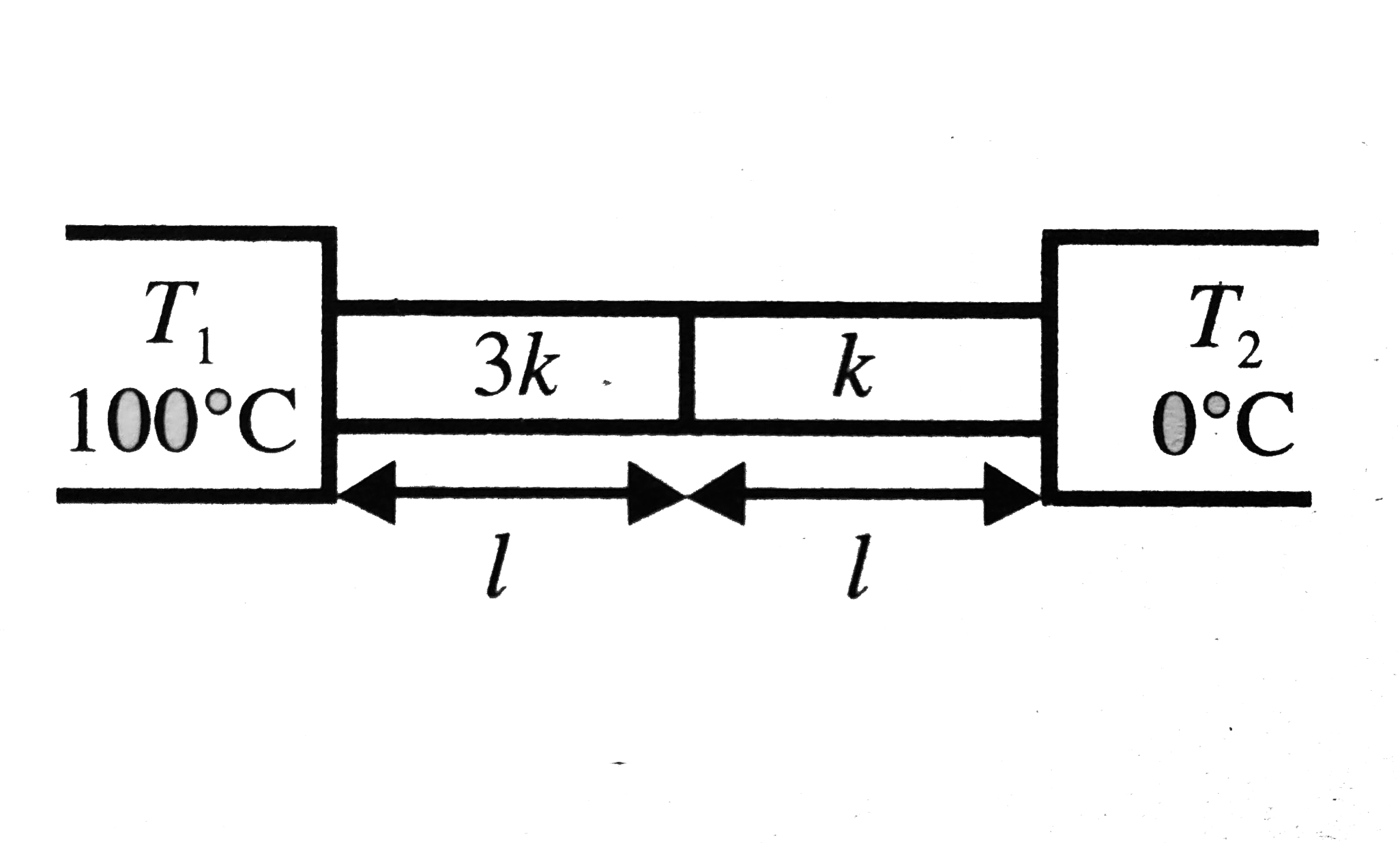
Two rods A and B of same length and cross-sectional area are connected in series and a temperature difference of 100∘C is maintained across the combination as shoen in Fig. If the thermal conductivity of the rod A is 3 k and that of rod B is k, Then
i.Determine the thermal resistance of each rod.
ii. determine the heat current flowing through each rod.
iii. determine the heat current flowing through each rod.
iv. plot the variation of temperature along the length of the rod.
View SolutionA solid body X of heat capacity C is kept in an atmosphere whose temperature is TA=300K. At time t=0 the temperature of X is T0=400K. It cools according to Newton's law of cooling. At time t1, its temperature is found to be 350K. At this time (t1), the body X is connected to a large box Y at atmospheric temperature is T4, through a conducting rod of length L, cross-sectional area A and thermal conductivity K. The heat capacity Y is so large that any variation in its temperature may be neglected. The cross-sectional area A of hte connecting rod is small compared to the surface area of X. Find the temperature of X at time t=3t1.
View Solution
