Three samples , and of the same gas have equal volumes and temperatures. The volume of each sample is doubled, the process being isothermal for , adiabatic for and isobaric for . If the final pressures are equal for the three samples, Find the ratio of the initial pressures.
= Initial pressure,
= Initial volume ,
=Final pressure,
= Final volume
Given ,
Isothermal work done
Adiabatic work done
Given that work done at both clases are same.
Hence,
...(1)
At adiabatic process,
From the equation (1)
and
So
or
Topper's Solved these Questions
Similar Questions
Three samples of the same gas A,B and C (γ=3/2) have initially equal volume. Now the volume of each sample is doubled. The process is adiabatic for A. Isobaric for B and isothermal for C. If the final pressures are equal for all three samples, find the ratio of their initial pressures
View SolutionThree samples A, B and C of the same gas (γ=1.5) have equal volumes and temperatures. The volume of each sample is doubled, the process being isothermal for A, adiabatic for B and isobaric for C. If the final pressures are equal for the three samples, Find the ratio of the initial pressures.
View Solution
Knowledge Check
Three samples of the same gas A,B and C (γ=3/2) have initially equal volume. Now the volume of each sample is doubled. The process is adiabatic for A. Isobaric for B and isothermal for C. If the final pressures are equal for all three samples, find the ratio of their initial pressures
A2:1:√2B2√2:1:2C√2:1:2D√2:2:1Three samples of the same gas A,B and C (γ=3/2) have initially equal volume. Now the volume of each sample is doubled. The process is adiabatic for A. Isobaric for B and isothermal for C. If the final pressures are equal for all three samples, find the ratio of their initial pressures
A2:1:√2B2√2:1:2C√2:1:2D√2:2:1
Two gases have the same initial pressure, volume and temperature. They expand to the same final volume, one adiabatically and the other isothermally
View SolutionThe absorption spectra of three samples A,B,C is given:
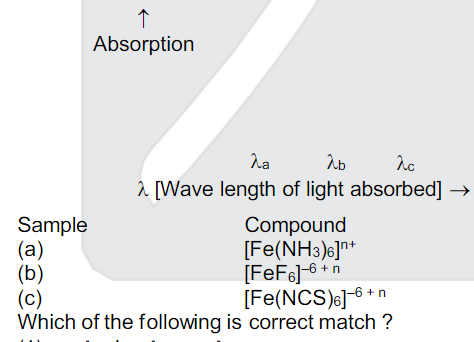
View SolutionIn a process on a system, the initial pressure and volume are equal to final pressure and volume, then
View SolutionA gas for which γ=1.5 is suddenly compressed to 1/4 th of the initial volume. Then the ratio of the final to initial pressure is
View SolutionThe volume of an ideal gas (γ=1.5) is changed adiabatically from 4.00 liters to 3.00 liters . Find the ratio of (a) the final pressure to the initial pressure and (b) the final temperature to the initial temperature.
View SolutionFor an ideal gas of fixed amount, the initial pressure and volume are equal to the final pressure and volume
View Solution
