Three solids of masses m1,m2 and m3 are connected with weightless string in succession and are placed on a frictionless table. If the mass m3 is dragged with a force T , the tension in the string between m2 and m3 is
m2m1+m2+m3T
m3m1+m2+m3T
m1+m2m1+m2+m3T
m2+m3m1+m2+m3T
The correct Answer is:C
To find the tension in the string between masses m2 and m3 when mass m3 is dragged with a force T, we can follow these steps:
Step 1: Understand the System
We have three masses m1, m2, and m3 connected by weightless strings on a frictionless table. When a force T is applied to m3, the entire system accelerates.
Step 2: Write the Equation for Total Acceleration
The total mass being accelerated is m1+m2+m3. According to Newton's second law, the net force applied to the system is equal to the total mass times the acceleration a:
T=(m1+m2+m3)⋅a
From this, we can express the acceleration a as:
a=Tm1+m2+m3
Step 3: Analyze the Forces on Each Mass
1. For mass m1:
The only force acting on m1 is the tension T1 in the string connected to it. Thus, we can write:
T1=m1⋅a
2. For mass m2:
The forces acting on m2 are the tension T2 from the string connected to m3 and the tension T1 from the string connected to m1. The equation becomes:
T2−T1=m2⋅a
3. For mass m3:
The forces acting on m3 are the applied force T and the tension T2 in the string connected to m2:
T−T2=m3⋅a
Step 4: Substitute a into the Equations
We can substitute a from Step 2 into the equations for T1, T2, and the equation for m3:
1. From T1:
T1=m1⋅Tm1+m2+m3
2. Substitute T1 into the equation for m2:
T2−m1⋅Tm1+m2+m3=m2⋅Tm1+m2+m3
Rearranging gives:
T2=m1⋅Tm1+m2+m3+m2⋅Tm1+m2+m3
T2=(m1+m2)Tm1+m2+m3
Final Result
Thus, the tension in the string between m2 and m3 is:
T2=(m1+m2)Tm1+m2+m3
We have three masses m1, m2, and m3 connected by weightless strings on a frictionless table. When a force T is applied to m3, the entire system accelerates.
The total mass being accelerated is m1+m2+m3. According to Newton's second law, the net force applied to the system is equal to the total mass times the acceleration a:
T=(m1+m2+m3)⋅a
From this, we can express the acceleration a as:
a=Tm1+m2+m3
1. For mass m1:
The only force acting on m1 is the tension T1 in the string connected to it. Thus, we can write:
T1=m1⋅a
The forces acting on m2 are the tension T2 from the string connected to m3 and the tension T1 from the string connected to m1. The equation becomes:
T2−T1=m2⋅a
The forces acting on m3 are the applied force T and the tension T2 in the string connected to m2:
T−T2=m3⋅a
We can substitute a from Step 2 into the equations for T1, T2, and the equation for m3:
1. From T1:
T1=m1⋅Tm1+m2+m3
T2−m1⋅Tm1+m2+m3=m2⋅Tm1+m2+m3
Rearranging gives:
T2=m1⋅Tm1+m2+m3+m2⋅Tm1+m2+m3
T2=(m1+m2)Tm1+m2+m3
Thus, the tension in the string between m2 and m3 is:
T2=(m1+m2)Tm1+m2+m3
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBOOK - ERRORLESS CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Critical Thinking
19 Videos
- NEWTONS LAWS OF MOTIONBOOK - ERRORLESS CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Graphical Questions
11 Videos
- NEWTONS LAWS OF MOTIONBOOK - ERRORLESS CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Equilibrium of Force
18 Videos
- MOTION IN TWO DIMENSIONBOOK - ERRORLESS CHAPTER - MOTION IN TWO DIMENSIONEXERCISE - Exercise
319 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on motion of connected mass)
10 Videos
Similar Questions
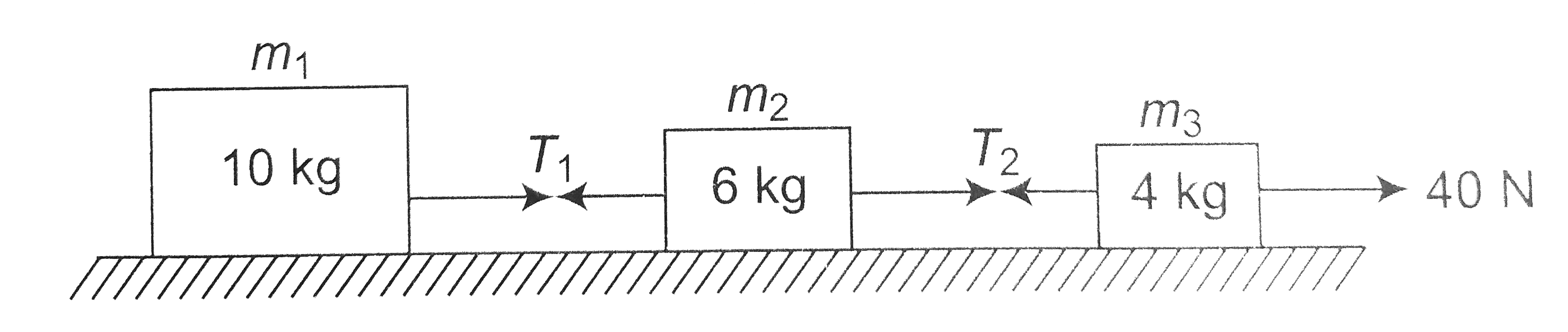
Three blocks of masses m1,m2andm3 are connected by mass less string as shown kept on a frictionless table.

They are pulled with a force T3=40N. If m1=10kg,m2=6kgandm3=4kg, the tension T2 will be
View SolutionThree blocks of masses m1,m2andm3 are connected by mass less string as shown kept on a frictionless table.

They are pulled with a force T3=40N. If m1=10kg,m2=6kgandm3=4kg, the tension T2 will be
View Solution
Knowledge Check
Three blocks of masses m1,m2and m3 are connected by massless strings as shown on a frictionless table. They are pulled with a force T3=40N. If m1=10kg,m2=6kg and m3=4kg the tension T2 will be
 A20 NB40 NC10 ND32 N
A20 NB40 NC10 ND32 NTwo bodies of masses m1 and m2 are connected a light string which passes over a frictionless massless pulley. If the pulley is moving upward with uniform acceleration g2, then tension in the string will be
A3m1m2m1+m2gBm1+m24m1m2gC2m1m2m1+m2gDm1m2m1+m2gThere blocks of masses m1 , m2 and m3 are connected by may less unstretchable strings on a smooth surface. Tension T2 is.
 A2.3NB32NC23ND3.2N
A2.3NB32NC23ND3.2N
Three blocks of masses m1,m2andm3 are connected by a massless string as shown in figure on a frictionless table. They are pulled with a force T3=40N. If m1=10kg,m2=6kgandm3=4kg, then tension T2 will be

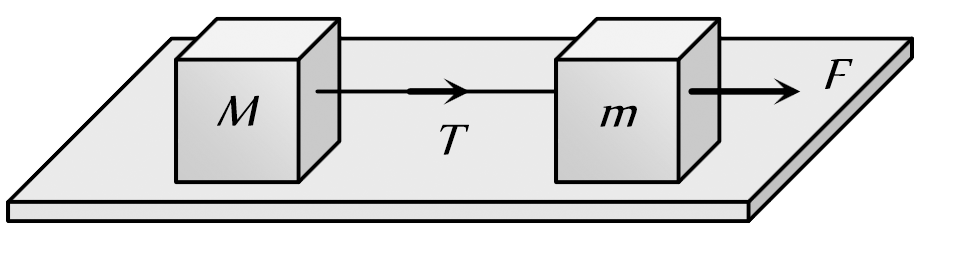
View SolutionTwo masses M and m are connected by a weightless string. They are pulled by a force F on a frictionless horizontal surface. The tension in the string will be
View SolutionThree masses M1,M2 and M3 are lying on a frictionless table. The masses are connected by massless threads as shown. The mass M3 is pulled by a constant force F as shown. The tension in the thread between masses M2 and M3 is

View SolutionThree block of masses m1,m2&M3 are connected by mass less stings as shown on a frictionless table.
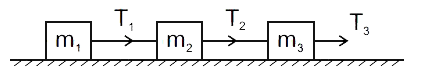
They are pulled with a force T3=40N, If m1=10kg,m2=6kg&m3=4kg, then tension T2 will be
View SolutionThree block of masses m1,m2 and m3 kg are placed in contact with each other on a frictionless table. A force F is applied on the heaviest mass m1, the acceleration of m2 will be

View Solution
