Three stars have surface temperatures and . A appaears bluish, B appears reddish and C appears yellowish. We can conclude that
The correct Answer is:A
To solve the problem regarding the surface temperatures of the stars A, B, and C based on their colors, we can follow these steps:
1. Identify the Color and Wavelength Relationship:
- The colors of the stars are given as follows:
- Star A appears bluish.
- Star B appears reddish.
- Star C appears yellowish.
- In terms of wavelength, blue light has a shorter wavelength, red light has a longer wavelength, and yellow light has a medium wavelength.
2. Understanding Wien's Displacement Law:
- Wien's Displacement Law states that the wavelength at which the emission of a black body spectrum is maximized (λ_max) is inversely proportional to the temperature (T) of the black body:
λmax⋅T=b
where b is Wien's displacement constant.
- This implies that:
λmax∝1T
- Therefore, a shorter wavelength corresponds to a higher temperature.
3. Assigning Temperatures Based on Color:
- Since star A appears bluish (shortest wavelength), it has the highest temperature TA.
- Star C appears yellowish (medium wavelength), so it has a temperature TC that is lower than TA but higher than TB.
- Star B appears reddish (longest wavelength), thus it has the lowest temperature TB.
4. Establishing the Temperature Order:
- From the above analysis, we can conclude:
TA>TC>TB
- This means:
- TA (blue star) is the highest.
- TC (yellow star) is in the middle.
- TB (red star) is the lowest.
Conclusion:
The final conclusion we can draw is that:
TA>TC>TB
- The colors of the stars are given as follows:
- Star A appears bluish.
- Star B appears reddish.
- Star C appears yellowish.
- In terms of wavelength, blue light has a shorter wavelength, red light has a longer wavelength, and yellow light has a medium wavelength.
- Wien's Displacement Law states that the wavelength at which the emission of a black body spectrum is maximized (λ_max) is inversely proportional to the temperature (T) of the black body:
λmax⋅T=b
where b is Wien's displacement constant.
- This implies that:
λmax∝1T
- Therefore, a shorter wavelength corresponds to a higher temperature.
- Since star A appears bluish (shortest wavelength), it has the highest temperature TA.
- Star C appears yellowish (medium wavelength), so it has a temperature TC that is lower than TA but higher than TB.
- Star B appears reddish (longest wavelength), thus it has the lowest temperature TB.
- From the above analysis, we can conclude:
TA>TC>TB
- This means:
- TA (blue star) is the highest.
- TC (yellow star) is in the middle.
- TB (red star) is the lowest.
The final conclusion we can draw is that:
TA>TC>TB
Topper's Solved these Questions
Similar Questions
The correct order for Ti,TB and TC is
View SolutionBoyle's temperature Tb is equal to
View SolutionFigure shows the isotherms of a fixed mass of an ideal gas at three temperatures TA,TB and TC , then
 View Solution
View SolutionThree bodies A,B and C have equal surface area and thermal emissivities in the ratio eA:eB:eC=1:12:14. All the three bodies are radiating at same rate. Their wavelengths corresponding to maximum intensity are αA,αB and αC respectively and their temperatures are TA,TB and TC on kelvin scale , then select the incorrect statement
View SolutionThree isothermal plots (P versus V) A, B and C are plotted at three temperature T1,T2andT3 respectively
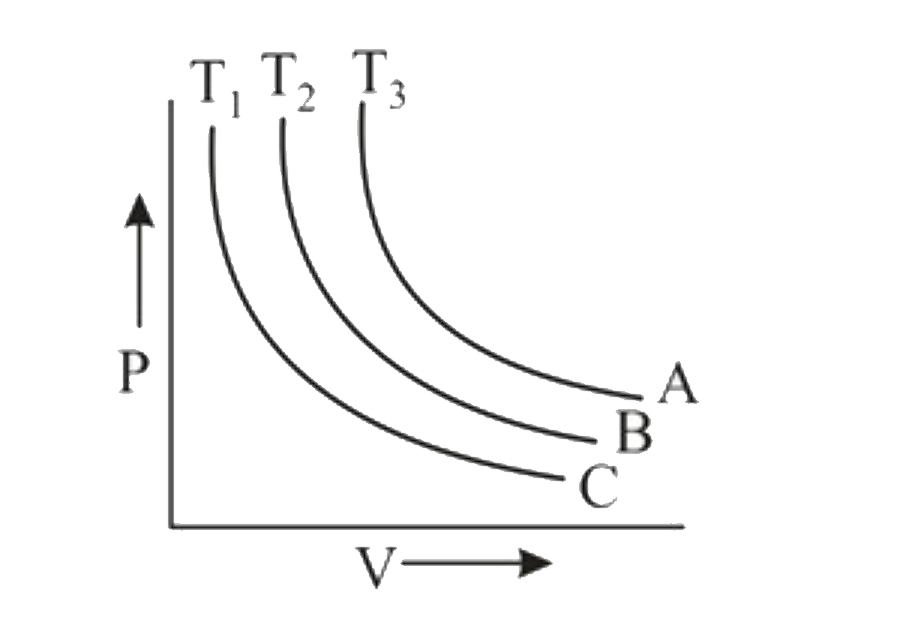
The correct order of the temperature will beView SolutionIf A- B = A and B- A=B , then what can we conclude ?
View SolutionTwo long ,thin,solid cylinders are identical in size, by they are made of different substances with two different thermal conductivities. The two cylinders are connected in series between a reservoir at temperature Thot and a reservoir at temperature Tcold.The temperature at the boundary between the two cylinders is Tb. One can conclude that:-
View SolutionCO2 at 600 bar and a temperature above Tc(Tc=304.15K) is called
View SolutionThree rods of equal length, area of cross section and thermal conductivity are connected as shown in the figure.

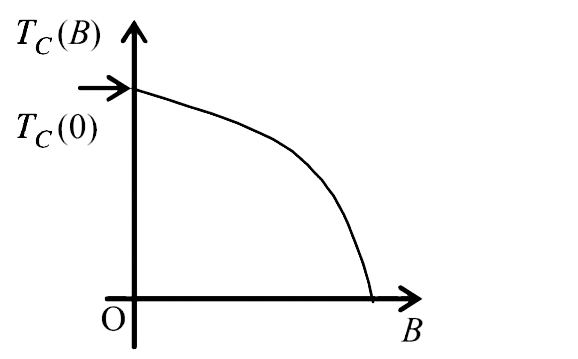
There is no heat loss through lateral surface of the rods and temperature of ends are TA=100∘C,TB=70∘C and TC=50∘C. Find the temperature of junction.View SolutionElectrical resistance of certain materials, known as superconductors, changes abruptly from a nonzero value of zero as their temperature is lowered below a critical temperature TC(0). An interesting property of super conductors is that their critical temperature becomes smaller than TC(0) if they are placed in a magnetic field, i.e., the critical temperature TC(B) is a function of the magnetic field strength B. The dependence of TC(B) on B is shown in the figure.
 .
.
A superconductor has TC(0)=100K. When a magnetic field of 7.5 Tesla is applied , its TC decreases to 75 K. For this material one can difinitely say that whenView Solution

