Three uniform spheres, A, B and C each of mass M and radius R are kept in such a way that each sphere touches the other two. What is the magnitude of the gravitational force acting on A due to B and C ?
√3GM24R2
√3GM2R2
3GM24R2
√3GM22R
The correct Answer is:A
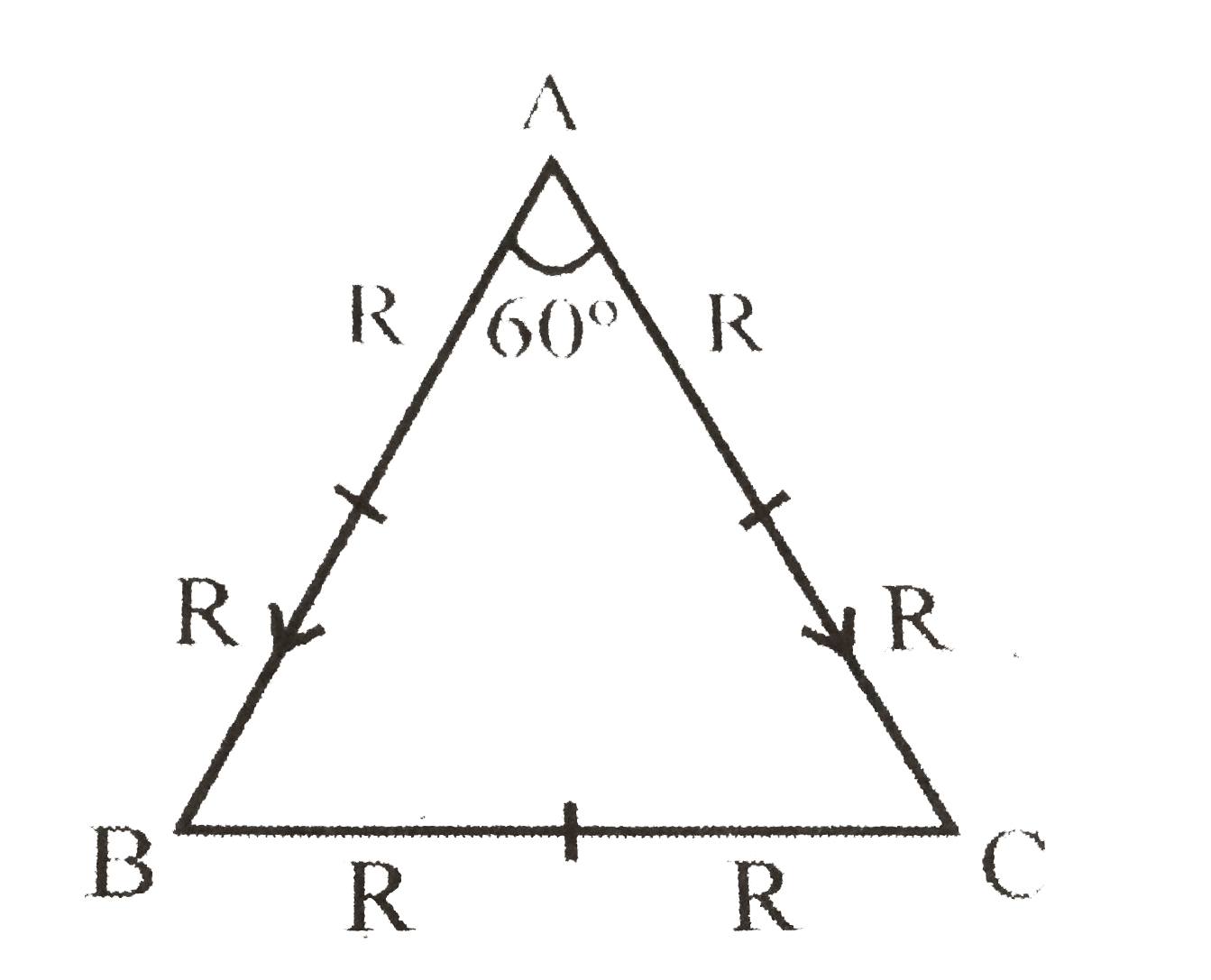
Assume that the mass of each sphere is concentrated at this centre. Then we have a system of three point masses situated at the vertices of an equilateral triangle. This force of attraction on A, due to sphere B is
F1=GM×M(2R)2=GM24R2 along −−→AB and the force on A due to sphere C is F2=GM24R2 along AC. Thus F1=F2 in magnitude, As angule between →F1 and →F2 is 60∘, the magnitude of the resultant force,
F=√F21+F22+2F1F2cos60∘
F=√F21+F21+2F1F1×12=√2F21+F21
∴F=√3F1=√3×GM24R2
Topper's Solved these Questions
- GRAVITATION BOOK - MARVEL PUBLICATIONCHAPTER - GRAVITATION EXERCISE - TEST YOUR GRASP -2
20 Videos
- ELECTROSTATICSBOOK - MARVEL PUBLICATIONCHAPTER - ELECTROSTATICSEXERCISE - TEST YOUR GRASP
20 Videos
- INTERFERENCE AND DIFFRACTIONBOOK - MARVEL PUBLICATIONCHAPTER - INTERFERENCE AND DIFFRACTIONEXERCISE - TEST YOUR GRASP
20 Videos
Similar Questions
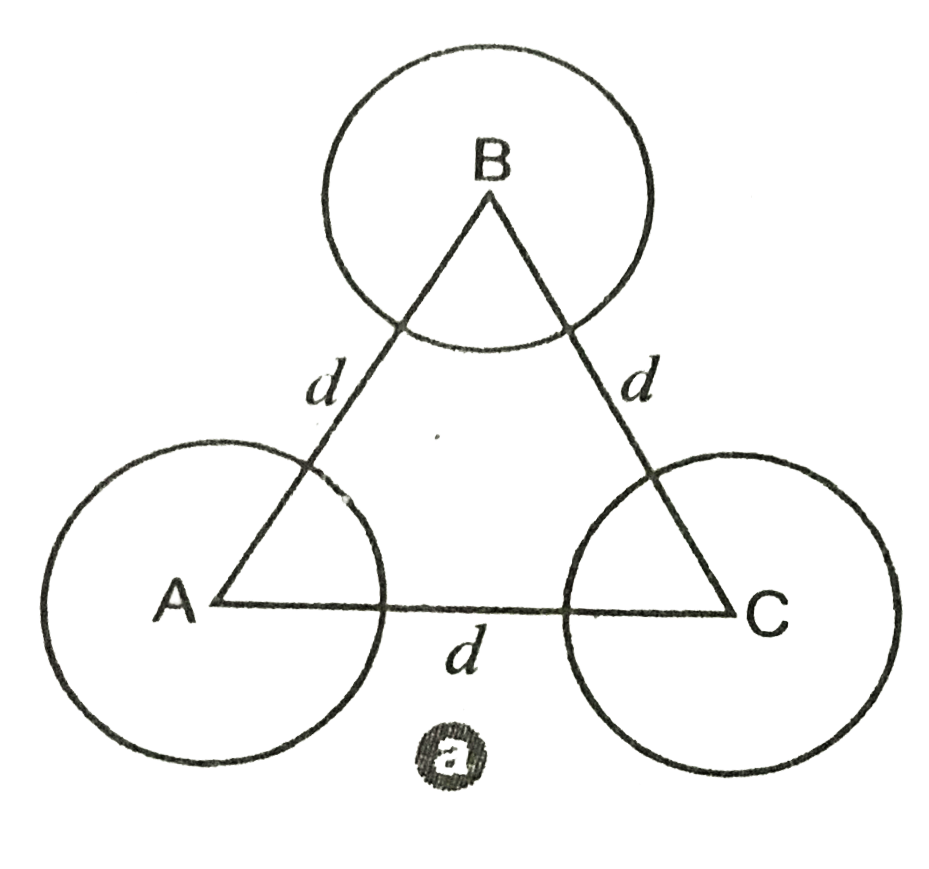
Thee uniform spheres each having a mass M and raius a are kept in such a way that each touches the other two. Find the magnitude of the gravitational force on any of the spheres due to the other two.
View SolutionThree uniform spheres, each having a mass M=5kg and radius a=2.5m are kept in such a way that each touches the other two. Find the magnitude of the gravitational force in GN on any of the spheres due to the other two.
View Solution
Knowledge Check
Three uniform spheres each of mass m and diameter D are kept in such a way that each touches the other two, then magnitudes of the gravitational force on any one sphere due to the other two is
A3Gm2D2B2√3Gm2D2C√3Gm24D2D√3Gm2D2Three identical spheres, each having a charge q and radius R. are kept in such a way that each touches the other two. The magnitude of the electric force on any sphere due to the other two is
A14πε0(qR)2B√34πε0(qR)2C√316πε0(qR)2D√516πε0(qR)2Two metal spheres each of radius r are kept in contact with each other. If d is the density of the material of the sphere,then the gravitational force between those spheres is proportional to
Ad2r6Bd2r4Cd2r4Dr2d2
Draw circles with centres A,B and C each of radius 3 cm, such that each circle touches the other two circles.
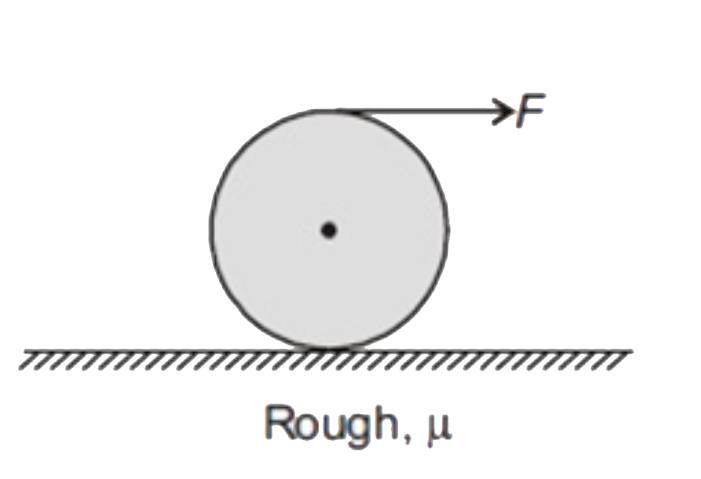
View SolutionA solid sphere of mass M and radius R is pulled by a force F as shown in figure . If the sphere does not slip over the surface , then frictional force acting on the sphere is
View SolutionThree solid spheres each of mass m and radius R are released from the position shown in Fig. What is the speed of any one sphere at the time of collision?
View SolutionThree spheres, each mass M and radius R, are arranged as shown in the figure . The moment of inertia of the system will be

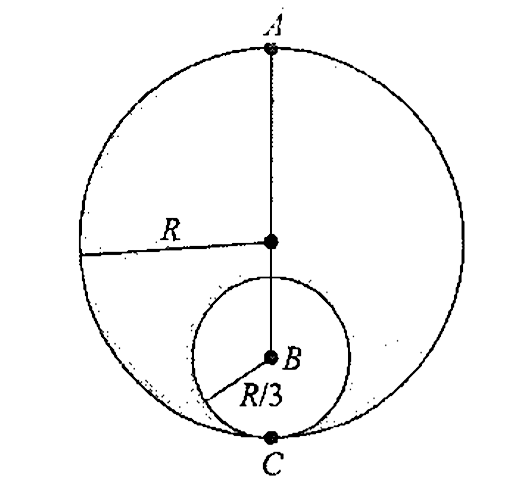
View SolutionInside a uniform sphere of mass M and radius R, a cavity of radius R/3, is made in the sphere as shown :
View Solution
