To double the torque acting on a coil of n-turns, when placed in a magnetic field
area of the coil and the magnetic induction should be doubled
area and current through the coil should be doubled
only area of coil should be doubled
number of turns are to be halved
The correct Answer is:C
To solve the problem of how to double the torque acting on a coil of n turns when placed in a magnetic field, we start with the formula for torque (τ) acting on a coil:
Step 1: Understand the formula for torque
The torque (τ) acting on a coil in a magnetic field is given by the formula:
τ=n×i×A×B×sin(θ)
where:
- n = number of turns in the coil
- i = current flowing through the coil
- A = area of the coil
- B = magnetic field strength
- θ = angle between the magnetic field and the normal to the coil
Step 2: Determine the condition for doubling the torque
To double the torque, we need to find a way to modify the parameters in the torque formula such that:
τ′=2τ
where τ′ is the new torque after modifications.
Step 3: Analyze the options
We will analyze each option provided in the question to see which one leads to doubling the torque.
Option 1: Area of the coil and magnetic induction should be doubled
If we double both the area (A) and magnetic field (B), the new torque becomes:
τ′=n×i×(2A)×(2B)×sin(θ)=4n×i×A×B×sin(θ)=4τ
This results in quadrupling the torque, so this option is incorrect.
Option 2: Area and current through the coil should be doubled
If we double both the area (A) and current (i), the new torque becomes:
τ′=n×(2i)×(2A)×B×sin(θ)=4n×i×A×B×sin(θ)=4τ
Again, this results in quadrupling the torque, so this option is also incorrect.
Option 3: Only area of the coil should be doubled
If we only double the area (A), the new torque becomes:
τ′=n×i×(2A)×B×sin(θ)=2n×i×A×B×sin(θ)=2τ
This results in exactly doubling the torque, so this option is correct.
Option 4: Number of turns are to be halved
If we halve the number of turns (n), the new torque becomes:
τ′=(n2)×i×A×B×sin(θ)=12n×i×A×B×sin(θ)=12τ
This results in halving the torque, so this option is incorrect.
Conclusion
The only option that correctly doubles the torque is:
Option 3: Only area of the coil should be doubled.
---
The torque (τ) acting on a coil in a magnetic field is given by the formula:
τ=n×i×A×B×sin(θ)
where:
- n = number of turns in the coil
- i = current flowing through the coil
- A = area of the coil
- B = magnetic field strength
- θ = angle between the magnetic field and the normal to the coil
To double the torque, we need to find a way to modify the parameters in the torque formula such that:
τ′=2τ
where τ′ is the new torque after modifications.
We will analyze each option provided in the question to see which one leads to doubling the torque.
If we double both the area (A) and magnetic field (B), the new torque becomes:
τ′=n×i×(2A)×(2B)×sin(θ)=4n×i×A×B×sin(θ)=4τ
This results in quadrupling the torque, so this option is incorrect.
If we double both the area (A) and current (i), the new torque becomes:
τ′=n×(2i)×(2A)×B×sin(θ)=4n×i×A×B×sin(θ)=4τ
Again, this results in quadrupling the torque, so this option is also incorrect.
If we only double the area (A), the new torque becomes:
τ′=n×i×(2A)×B×sin(θ)=2n×i×A×B×sin(θ)=2τ
This results in exactly doubling the torque, so this option is correct.
If we halve the number of turns (n), the new torque becomes:
τ′=(n2)×i×A×B×sin(θ)=12n×i×A×B×sin(θ)=12τ
This results in halving the torque, so this option is incorrect.
The only option that correctly doubles the torque is:
Option 3: Only area of the coil should be doubled.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IB71videos
MOVING CHARGES AND MAGNETISM
- BOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-II79videos
MOVING CHARGES AND MAGNETISM
- BOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-III49videos
MOVING CHARGES AND MAGNETISM
- BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question15videos
MOTION IN A STRAIGHT LINE
- BOOK - AAKASH SERIESCHAPTER - NUCLEAR PHYSICSEXERCISE - ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED) Integer Type Questions3videos
NUCLEAR PHYSICS
Similar Questions
(a) Derive the expression for the torque acting on a current carrying placed in a magnetic field.
(b) Explain the significance of a radial magnetic when current carrying coil is kept in it.View SolutionDeduce an expression for torque acting on a bar magnet placed in uniform external magnetic field.
View SolutionTorque acting on a current loop in a uniform magnetic field is equal to
View SolutionA circular coil of 20turns and radius 10cm carries a current of 5A. It is placed in a uniform magnetic field of 0⋅10T. Find the torque acting on the coil when the magnetic field is applied (a) normal to the plane of the coil (b) in the plane of coil. Also find out the total force acting on the coil.
View SolutionThe rectangular coil having 100 turns is placed in a uniform magnetic field of (0.05√2)ˆj tesla as shown in Fig. 1.84. Find the torque acting on the loop.
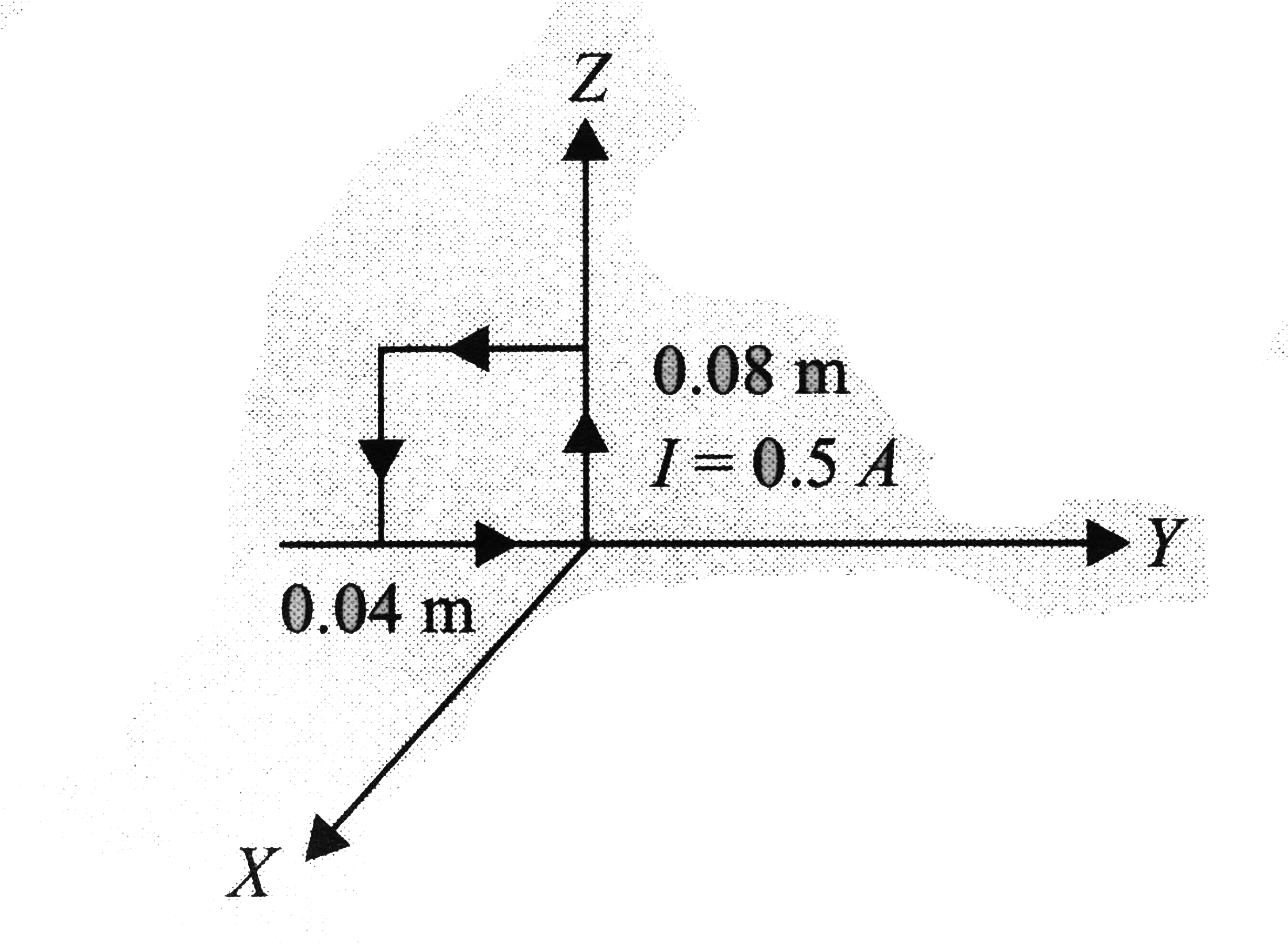 View Solution
View SolutionCurrent I is flowing through a circular coil of radius r. It is placed in a magnetic field B in such a way that the plane of the circular coil is perpendicular to B. The force acting on it will be -
View SolutionA coil of cross-sectional area A having n turns is placed in uniform magnetic field B. When it is rotated with an angular velocity ω, the maximum e.m.f. induced in the coil will be :
View SolutionThe magnetic field at the centre of a circular coil carrying current I ampere is B. It the coil is bent into smaller circular coil of n turns then its magnetic field at the centre is B, the ratio between B' and B is
View SolutionA coil carrying electric current is placed in uniform magnetic field
View SolutionA long wire carrying a steady current is bent into a circular loop of one turn. The magnetic field at the centre of the loop is B. it is then bent into a circular coil of n turns. The magnetic field at the centre of this coil of n turns will be
View Solution

