Torque acting on a particle about an arbitrary origin is zero, What can be said about the angular momentum of the particle about the origin ?
To solve the question regarding the relationship between torque and angular momentum, let's break it down step by step.
1. Understanding the Given Information:
- We are given that the torque acting on a particle about an arbitrary origin is zero.
- Mathematically, this can be expressed as:
τ=0
where τ is the torque.
2. Recall the Relationship Between Torque and Angular Momentum:
- The relationship between torque and angular momentum (L) is given by the equation:
τ=dLdt
This means that the torque is equal to the rate of change of angular momentum with respect to time.
3. Substituting the Given Value of Torque:
- Since we know that the torque τ is zero, we can substitute this into the equation:
0=dLdt
4. Analyzing the Equation:
- The equation 0=dLdt implies that the rate of change of angular momentum is zero.
- This means that the angular momentum L is not changing with time.
5. Conclusion:
- If the angular momentum is not changing, it must be constant. Therefore, we can conclude that:
L=constant
This means that the angular momentum of the particle about the origin remains constant when the torque is zero.
Final Answer:
When the torque acting on a particle about an arbitrary origin is zero, the angular momentum of the particle about that origin is constant.
---
- We are given that the torque acting on a particle about an arbitrary origin is zero.
- Mathematically, this can be expressed as:
τ=0
where τ is the torque.
- The relationship between torque and angular momentum (L) is given by the equation:
τ=dLdt
This means that the torque is equal to the rate of change of angular momentum with respect to time.
- Since we know that the torque τ is zero, we can substitute this into the equation:
0=dLdt
- The equation 0=dLdt implies that the rate of change of angular momentum is zero.
- This means that the angular momentum L is not changing with time.
- If the angular momentum is not changing, it must be constant. Therefore, we can conclude that:
L=constant
This means that the angular momentum of the particle about the origin remains constant when the torque is zero.
When the torque acting on a particle about an arbitrary origin is zero, the angular momentum of the particle about that origin is constant.
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - PROBLEMS TOUGH & TRICKY
8 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - NCERT FILE ( NCERT TEXTBOOK EXERCISES )
21 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - PRACTICE PROBLEMS
26 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
- THERMAL PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
The moment of Inertia of a particle about an axis of rotation is 0.2kgm2 .If the angular momentum of the particle about the axis is 0.4kgm2s ,then what is the rotational kinetic energy of the particle?
View SolutionA particle is acted on by two torques about the origin: →τ1 has a magnitude of 2.0N⋅m and is directed in the positive direction of the x axis, and →τ2 has a magnitude of 3.0N⋅m and is directed in the nagative direction of the y axis. In unit-vector notation, find →dl/dt, where →l is the angular momentum of the particle about the origin.
View Solution
Knowledge Check
A particle is moving parallel to x-axis as shown in the figure. The angular velocity of the particle about the origin is
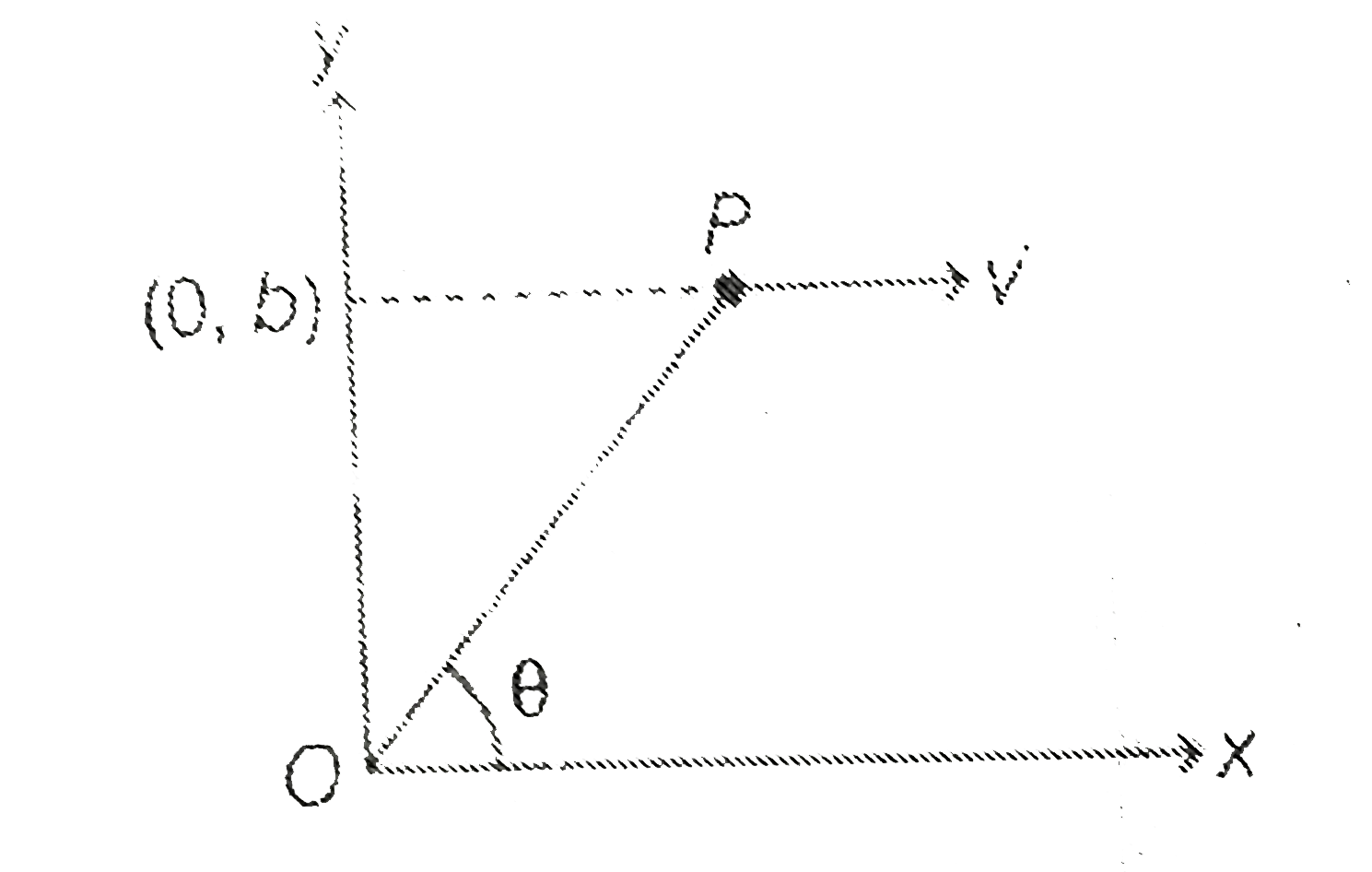 A(v/b)sin2θB(v/b)C(v/b)sinθDvbsinθ
A(v/b)sin2θB(v/b)C(v/b)sinθDvbsinθA particle of mass m moves along line PC with velocity v as shown. What is the angular momentum of the particle about O?
 AmvLBmvlCmvrDZero
AmvLBmvlCmvrDZeroA particle is moving in a horizontal uniform circular motion. The angular momentum of the particle is conserved about the point :
ACentre of the circleBOutside the circleCInside the circleDPoint on circumference
A particle of mass m moves along line PC with velocity v as shown. What is the angular momentum of the particle about P?
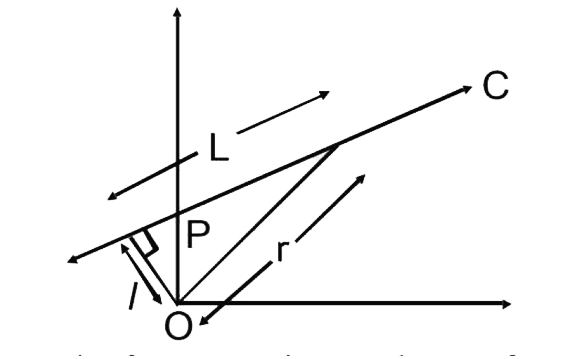
View SolutionA particle of mass m moves along line PC with velocity v as shown. What is the angular momentum of the particle about O?

View SolutionA particle of mass m=5 unit is moving with a uniform speed v=3√2 unit in the XOY plane along the line y=x+4 the magnitude of the angular momentum of the particle about the origin is
View SolutionA particle of mass m=5 unit is moving with a uniform speed v=3√2 unit in the XOY plane along the line y=x+4 the magnitude of the angular momentum of the particle about the origin is
View SolutionA particle of mass m = 5 units is moving with a uniform speed v=3√2 units in the XOY plane along the line Y = X + 4. The magnitude of the angular momentum of the particle about the origin is
View Solution
