Question

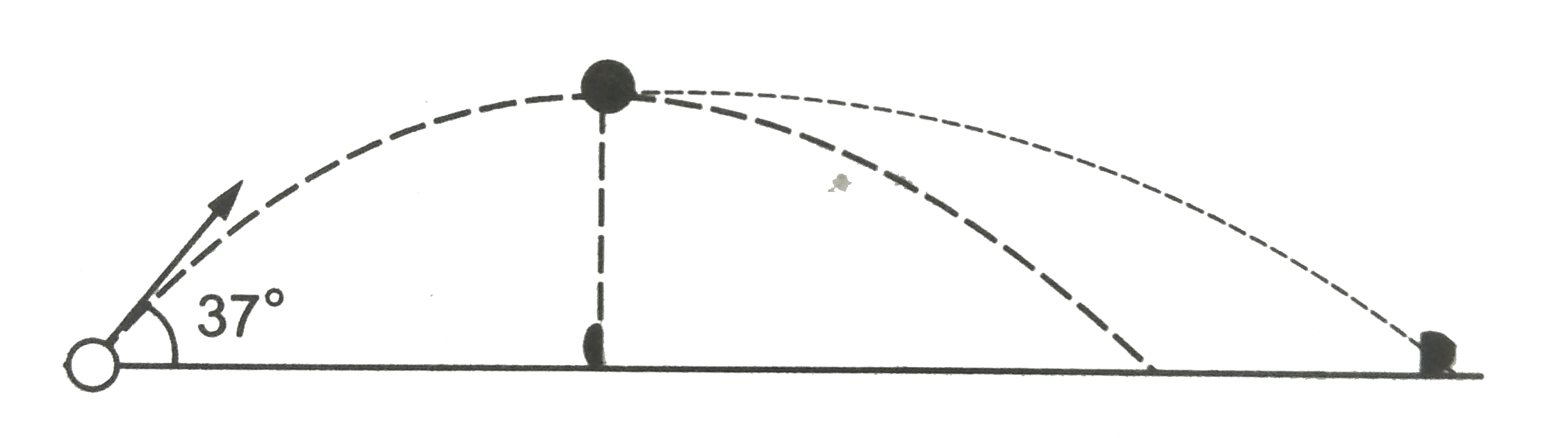
A body is projected with a speed 160 m/s at an angle ${53}^{\circ }$ with the horizontal, At the highest point, body explodes into two pieces with mass ratio 1:3. Smaller piece comes to rest immediately after explosion. Find the distance of point from point of projection where heavier piece strikes the horizontal surface.

Explanation

To solve the problem step by step, we will follow the procedure outlined in the video transcript.

Step 1: Identify the given data
- Initial speed \( u = 160 \, \text{m/s} \)
- Angle of projection \( \theta = 53^\circ \)
- Mass ratio of the two pieces after explosion \( m_1:m_2 = 1:3 \)

Step 2: Calculate the range of the projectile before the explosion
The formula for the range \( R \) of a projectile is given by:
\( R = \frac{u^2 \sin(2\theta)}{g} \)
Where:
- \( g = 10 \, \text{m/s}^2 \) (acceleration due to gravity)

First, we calculate \( \sin(2\theta) \):
\( \sin(2 \times 53^\circ) = \sin(106^\circ) \approx 0.961 \)

Now substituting the values into the range formula:
\( R = \frac{(160)^2 \cdot 0.961}{10} \)
\( R = \frac{25600 \cdot 0.961}{10} = 2456.96 \, \text{m} \approx 2160 \, \text{m} \)

Step 3: Understand the explosion and the motion of the pieces
At the highest point of the projectile's motion, the body explodes into two pieces:
- The smaller piece (mass \( m_1 \)) comes to rest immediately after the explosion.
- The heavier piece (mass \( m_2 \)) continues to move.

Step 4: Calculate the center of mass of the system
Since the smaller piece comes to rest, the center of mass of the system will continue to follow the same trajectory as before the explosion. The center of mass \( X_{cm} \) can be calculated as:
\( X_{cm} = \frac{m_1 x_1 + m_2 x_2}{m_1 + m_2} \)
Where:
- \( m_1 = \frac{M}{4} \) (smaller piece)
- \( m_2 = \frac{3M}{4} \) (heavier piece)
- \( x_1 = R/2 = 1080 \, \text{m} \) (distance covered by the smaller piece)

Step 5: Solve for the distance \( x_2 \) of the heavier piece
Substituting the known values into the center of mass equation:
\( 2160 = \frac{\left(\frac{M}{4}\right) \cdot 1080 + \left(\frac{3M}{4}\right) x_2}{M} \)
This simplifies to:
\( 2160 = \frac{270M + \frac{3M}{4} x_2}{M} \)
\( 2160 = 270 + \frac{3}{4} x_2 \)
Now, isolating \( x_2 \):
\( 2160 - 270 = \frac{3}{4} x_2 \)
\( 1890 = \frac{3}{4} x_2 \)
Multiplying both sides by \( \frac{4}{3} \):
\( x_2 = 1890 \cdot \frac{4}{3} = 2520 \, \text{m} \)

Final Result
The distance from the point of projection where the heavier piece strikes the horizontal surface is:
\( \boxed{2520 \, \text{m}} \)