Tow identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrum position by a distance x towards right, find the restoring force.

Consider the diagram in which the block is displaced right through x.
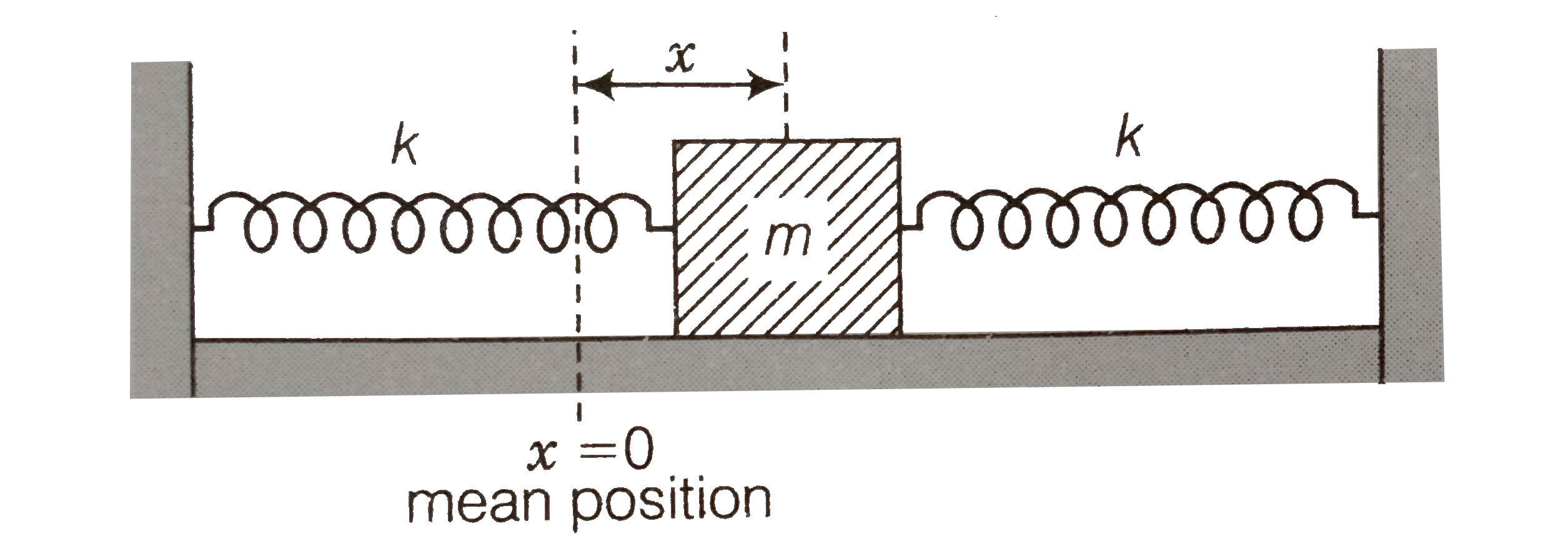
The right spring gets compressed by x developing a restoring force k x towards left on the block. The left speing is stretched by an amout x developing a restoring force k x towards left on the block as gven in the free body diagram of the block.

Hence, total force (restoring) =(kx+kx) [∵Both forces are in same direction]
2kx towardsleft
Topper's Solved these Questions
Similar Questions
Two identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure. When the mass is displaced from equilibrium position by a distance x towards right, find the restoring force.

View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View Solution
Knowledge Check
A block of mass m is connected to two indentical springs of spring constant k which are in turn connected to fixed supports as shown in the figure. Find the time period for small oscillations of the block.
 A2π√mkB2π√m2kC2π√2mkDπ√m2k
A2π√mkB2π√m2kC2π√2mkDπ√m2kSpring of spring constant k is attached with a block of mass m1, as shown in figure. Another block of mass m2 is placed angainst m1, and both mass masses lie on smooth incline plane.

Find the compression in the spring when lthe system is in equilibrium.A(m1+m2)gsinθ2kB(m1+m2)gsinθkC(m1+m2)gkD2(m1+m2)gsinθkTwo springs, each of spring constant k, are attached to a block of mass m as shown in the figure. The block can slide smoothly alongs a horizontal platform clamped to the oppsite walls of the trolley of mass M. If the block is displaced by xcm and released, the period of oscillaion is :
 AT=2π√Mm2kBT=2π√(M+m)kmMCT=2π√mM2k(M+m)DT=2π(M+m)k
AT=2π√Mm2kBT=2π√(M+m)kmMCT=2π√mM2k(M+m)DT=2π(M+m)k
Two identical springs of spring constant k are attached to a block of mass m and to fixed supports as shwon in figure . Show that when the mass is displaced from its equilibrium position on either side, it executes a simple harmonic motion. Find th eperiod of oscillation.

View SolutionTwo identical springs of spring constant '2k' are attached to a block of mass m and to fixed support (see figure).When the mass is displaced from equilibrium position on either side, it executes simple harmonic motion. The time period of oscillations of this sytem is :

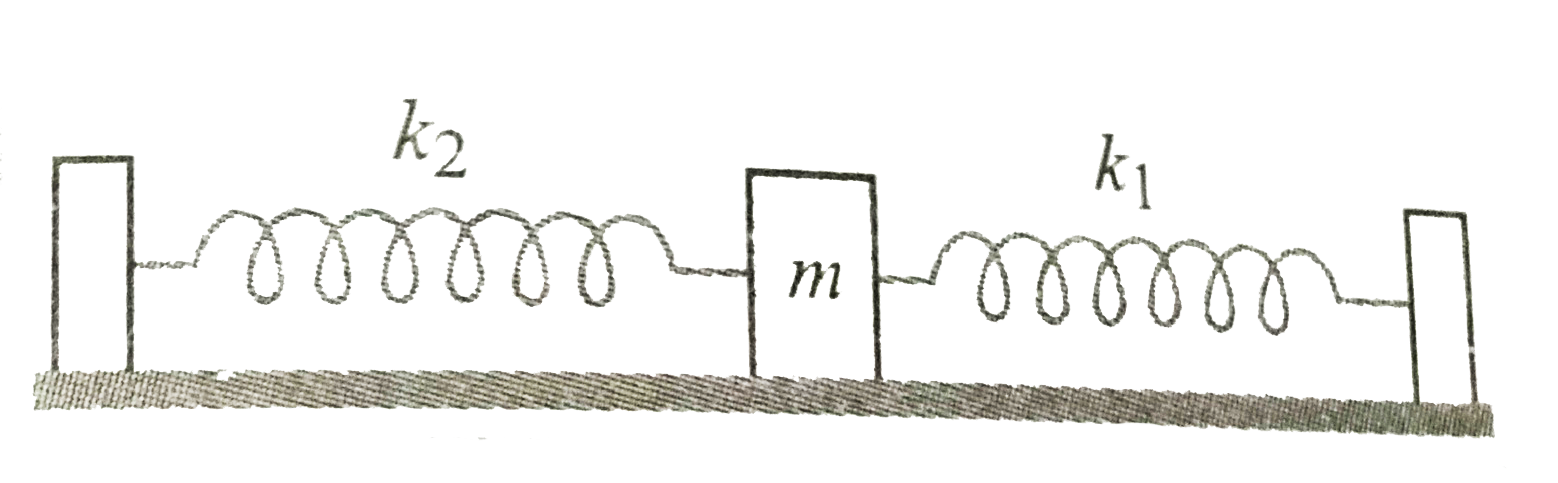
View SolutionTwo spring have force constants k1 and k2 respectively. They are attached to a mass m and two fixed supports as shwon in figure. If the surface is frictionless, fing the time period of oscillations. What is the spring factore of this combination.
View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionA mass 1 kg is attaced to the hook of a spring and the spring is suspended vertically from a ceiling (see Fig. 5.12a). The spring is displaced from its equilibrium position by a distance x. The spring constant of the spring is 2.0×102 N/m. Calculate the displacement x.
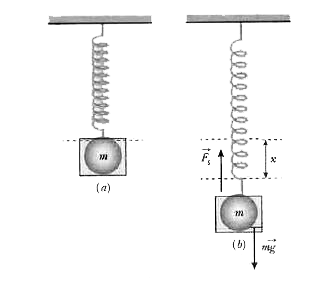
Figure 5-12 (a) Mass of 1 kg attached to a spring is suspended vertically. (b) Spring displace from equilibrium position by a distance x.
View Solution
