Twelve identical resistances arranged on all edges of a cube. The resistors are all the same. Then find the equivalent resistance between the edges A and B as shown in figure.

Video Solution
Text Solution
a. Between 1 and 4: Points 2 and 5 are symmetrically located w.r.t points 1 and 4. so, they are at same potentials
similarly points 3 and 8 also symmetircally located w.r.t point 1 and 4. So they are again at same potential. Now, we have 12 resistors each of resistance r connected across 1 and 2, 2 and 3,...., etc. So redrawing them wiht the assumption that 2 and 5 are at same ptential and 3 and 8 are at same potential. The new figure is a shown in figure.
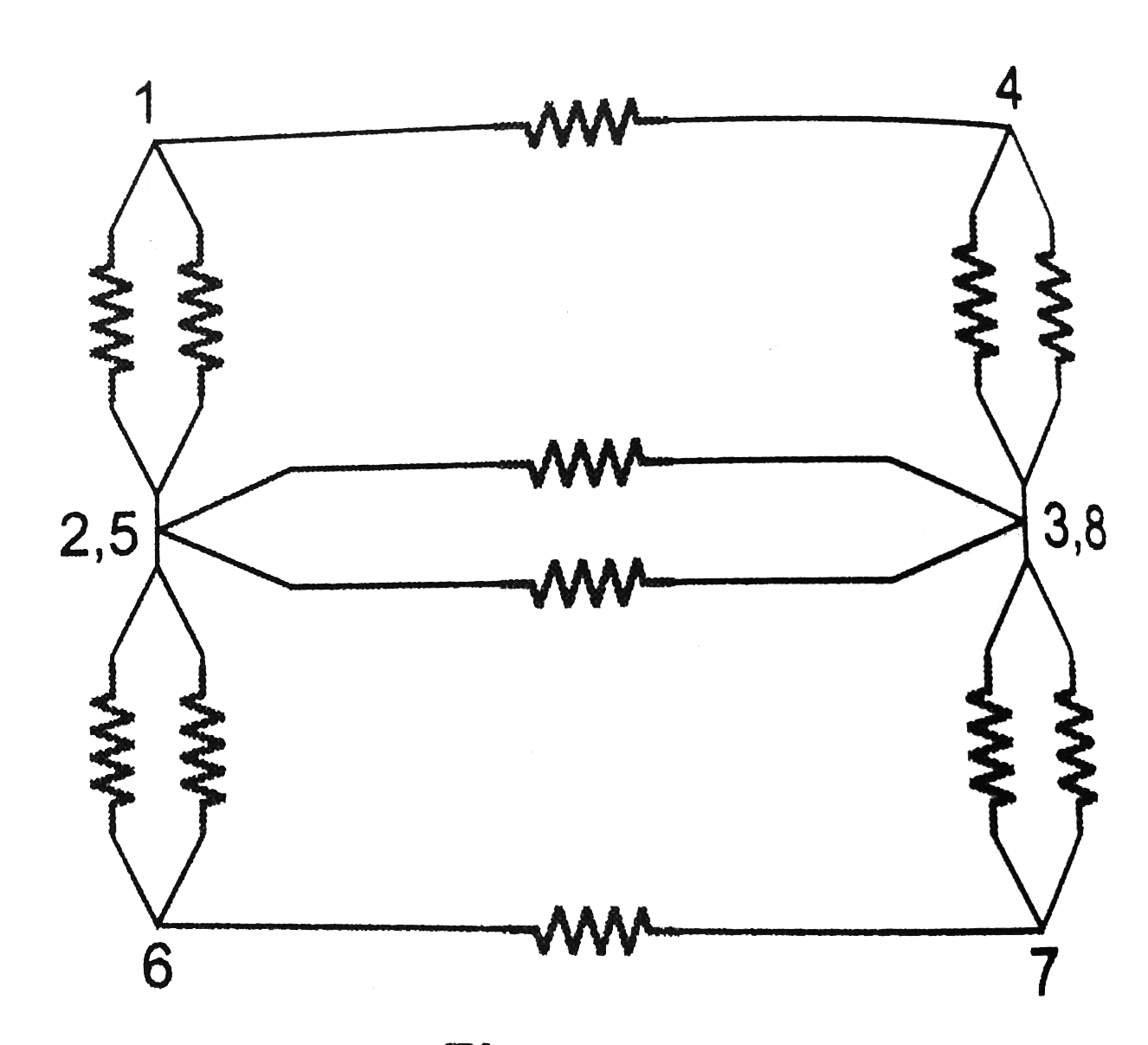
Now we had to find the equivalent resistance between ltbr> 1 and 4. We can now simplify the circuit as
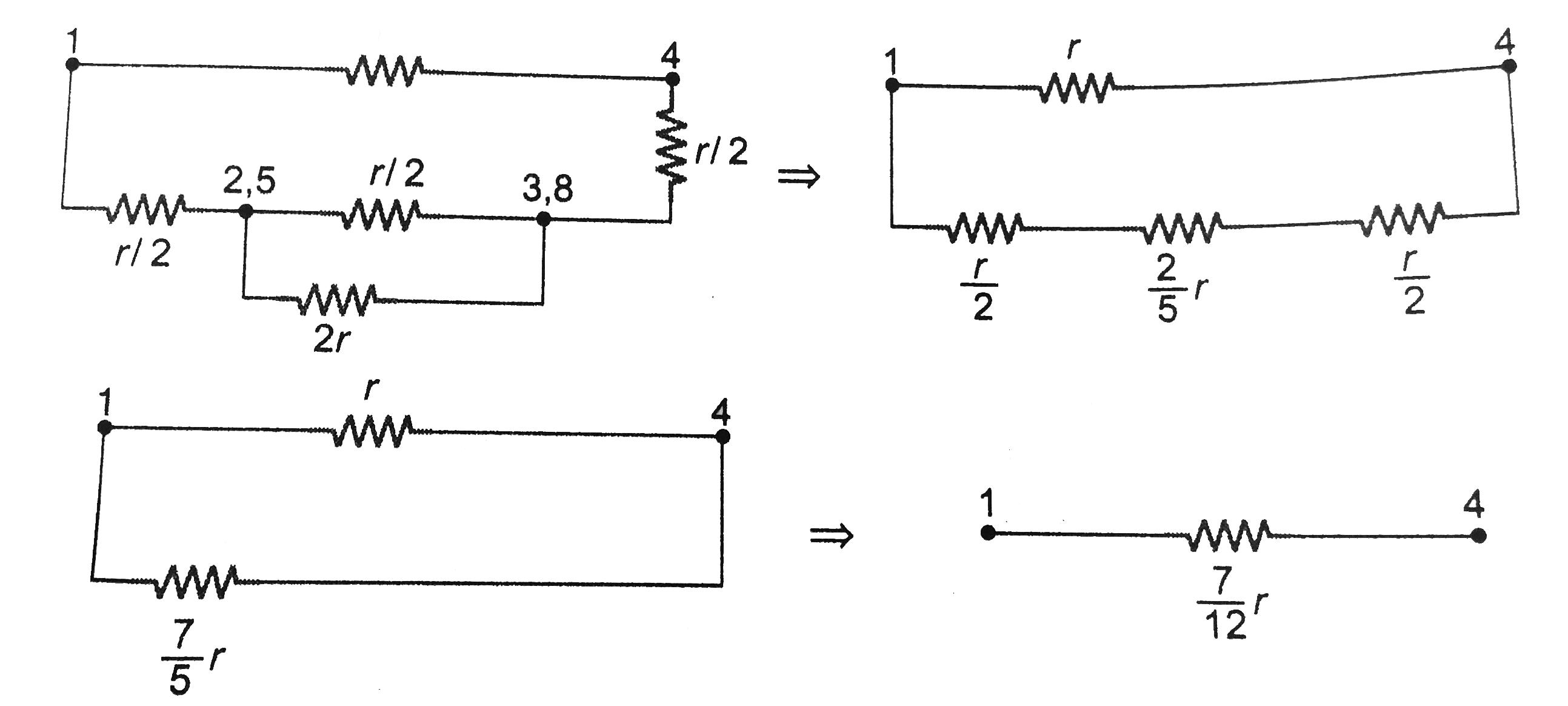
Thus, the equivalent resistance between points 1 and 4 is 712r.
b. Between 1 and 3: Points 6 and 8 are symmetrically located w.r.t points 1 and 3. Similarly points 2 and 4 are located symmetrically w.r.t points 1 and 3. So, points 6 and 8 are at the same potential. similarly 2 and 4 are at same potentials. Redrawing the simple circuit we have figure. 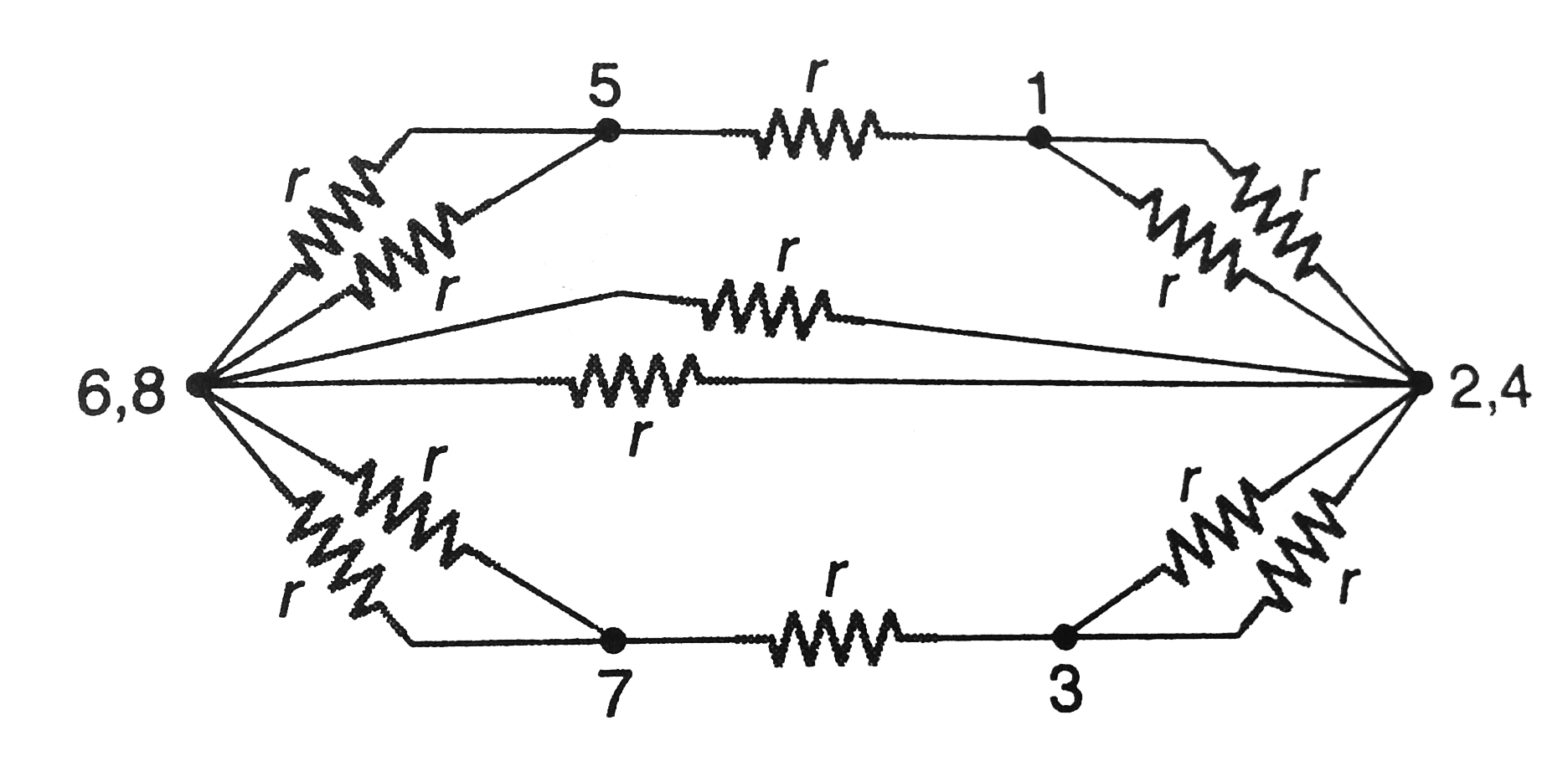
Between 1 and 3, a balanced Wheatstone bridge is formed as shown in figure. So, the resistance betwen 2 and 6 and between 4 and 8 can be removed.
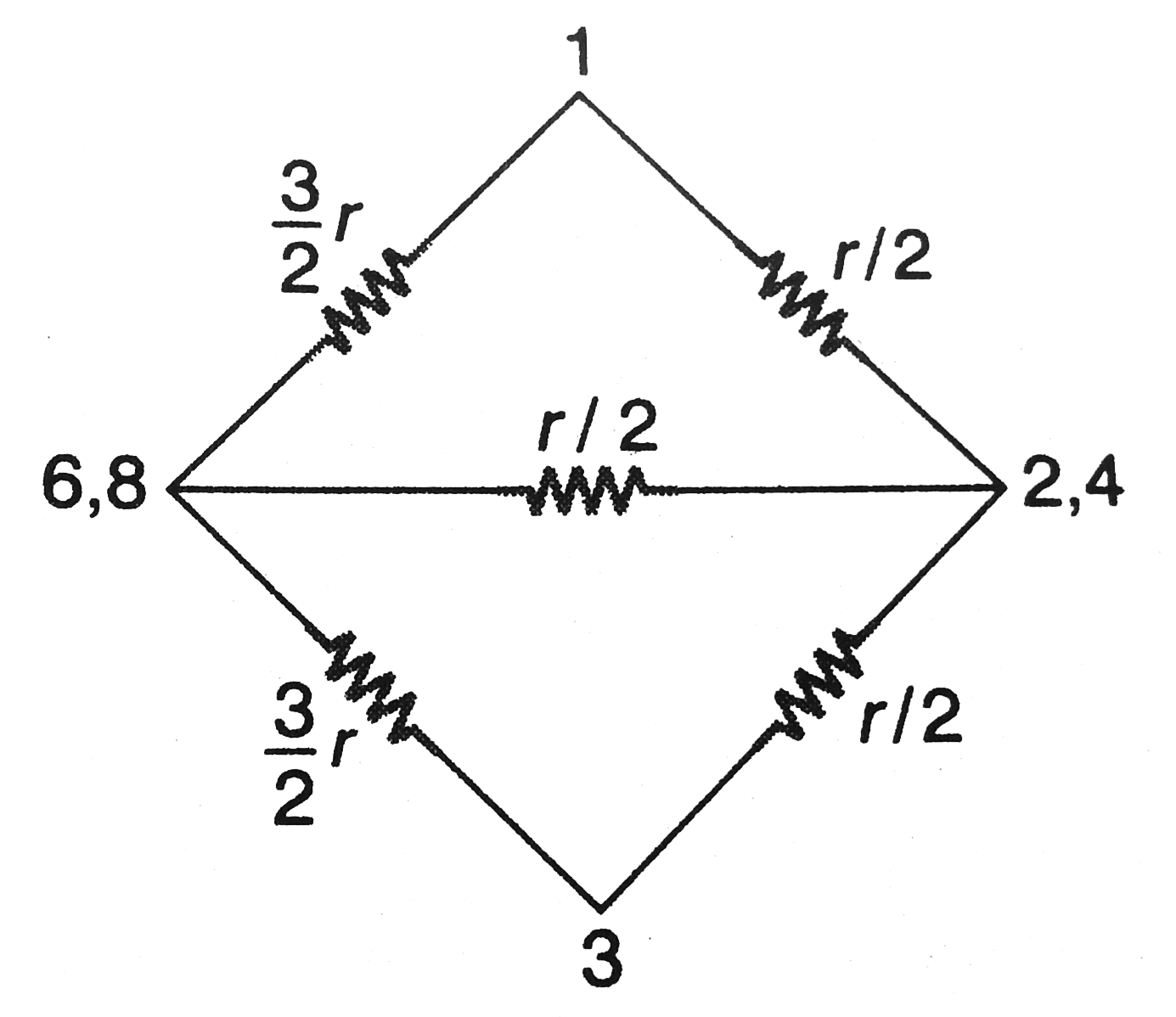
Thus, the equivalent resistance between 1 and 3 is 34r
|
Topper's Solved these Questions
- CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - Exercise
155 Videos
- CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Videos
- ATOMSBOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY
42 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
Similar Questions
Knowledge Check
The equivalent resistance between A and B for . the circuit shown in this figure is
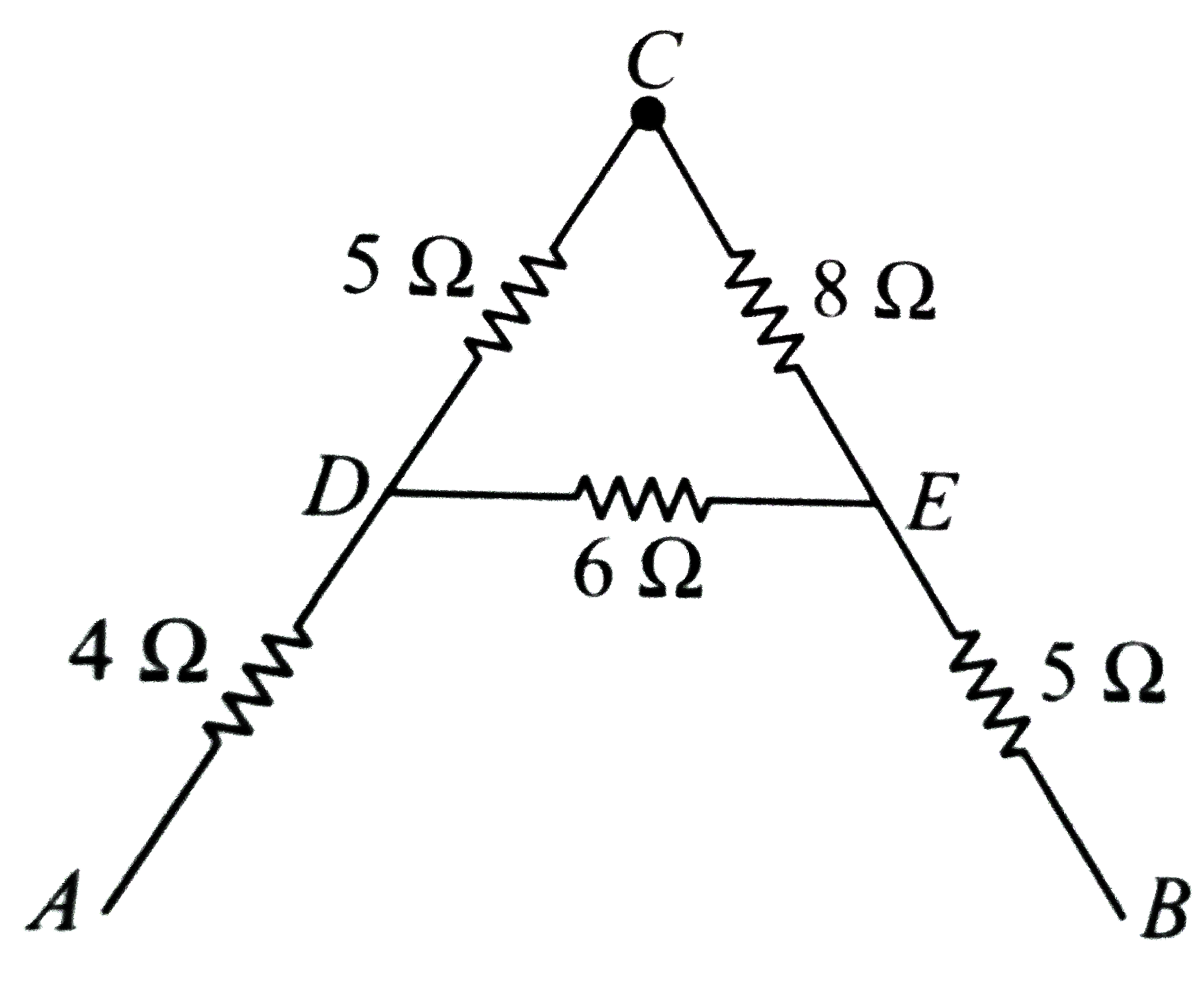 A13.1ΩB15.1ΩC17.1ΩD19.1Ω
A13.1ΩB15.1ΩC17.1ΩD19.1Ω
Find the equivalent resistance between A and B in the given figure.
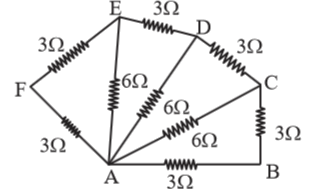
View SolutionFind the equivalent resistance between A and B in the give figure .
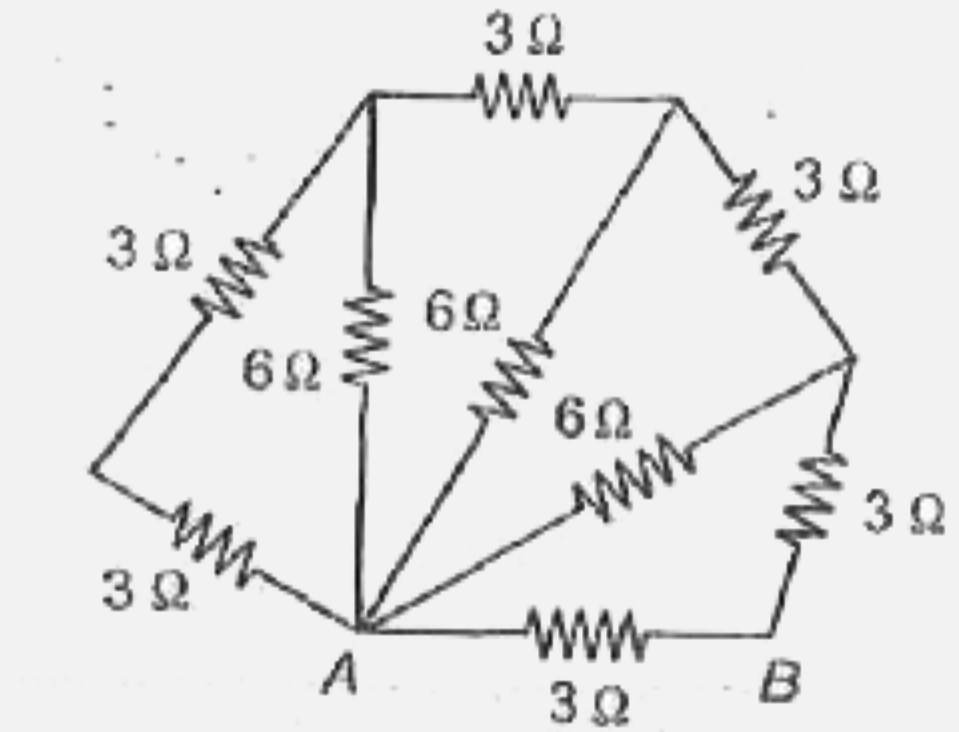
View SolutionThe equivalent resistance between point A and B in the circuit shown in figure is
_PHY_E05_041_Q01.png)
View SolutionThe equivalent resistance between points A and B in the circuit shown in figure is
_PHY_E05_095_Q01.png)
View SolutionIn the same figure, equivalent resistance between points A and D is
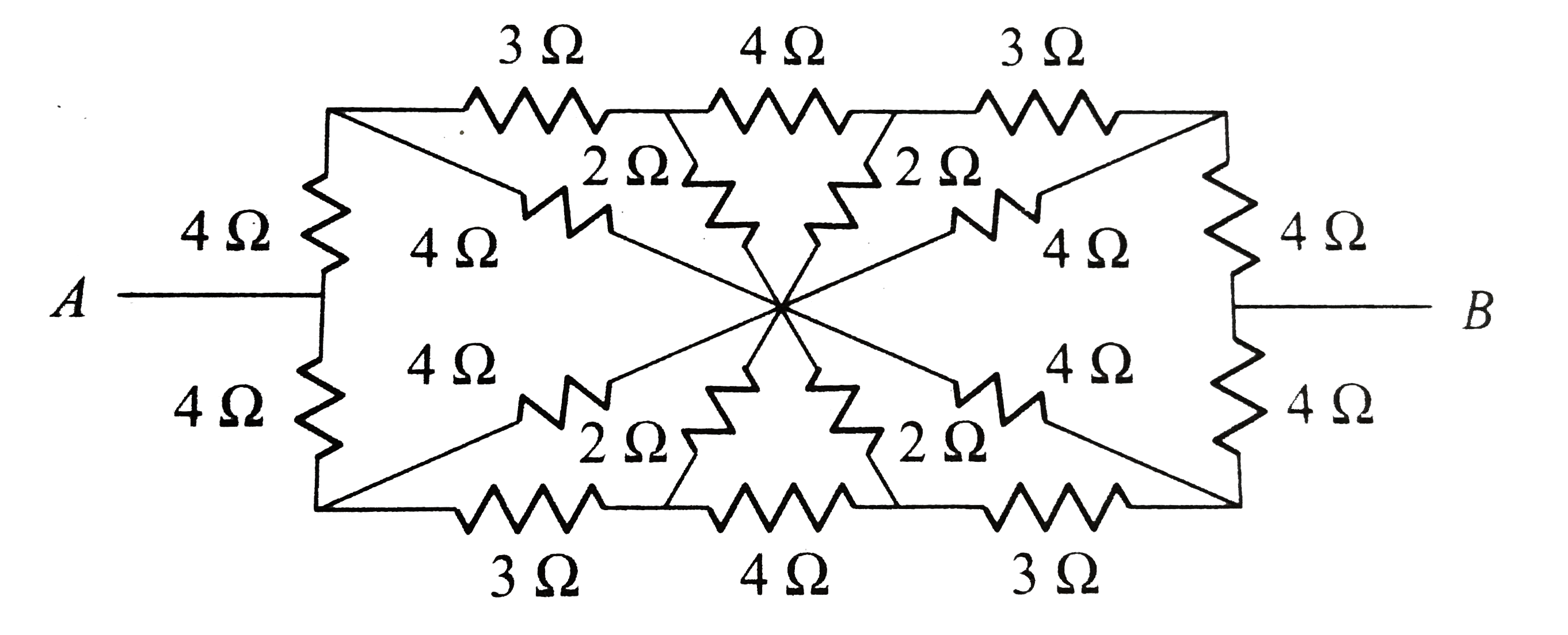
View SolutionA number of resistors are connected as shown in the figure. The equivalent resistance between A and B is
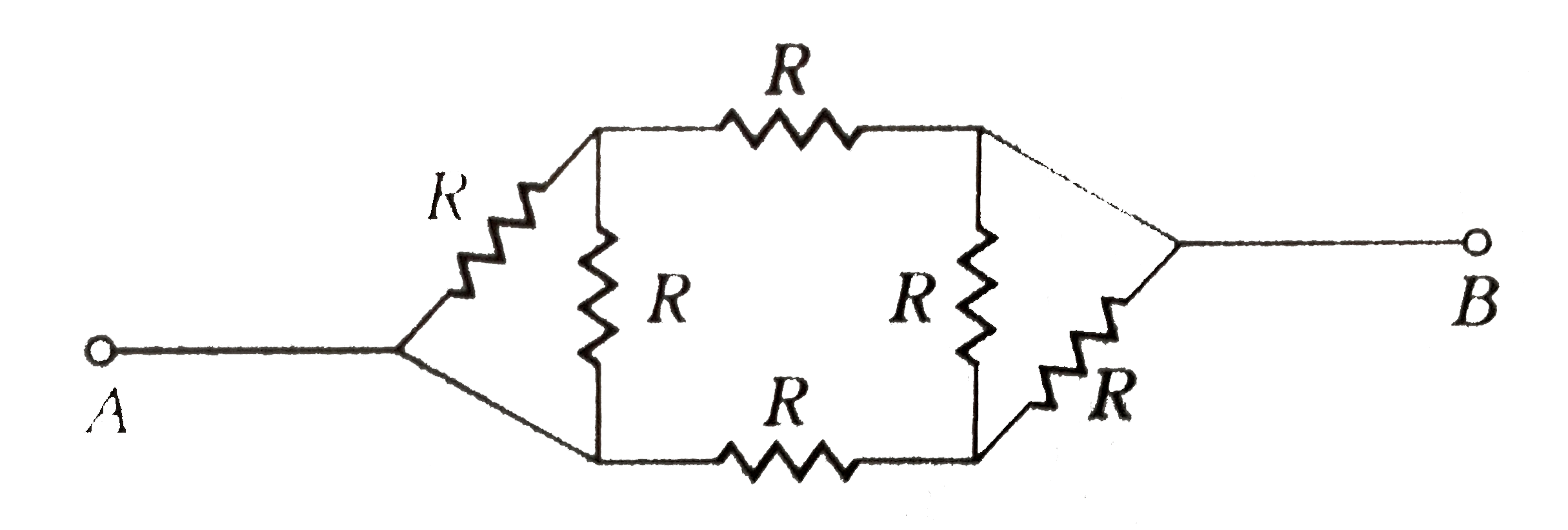
View SolutionThe equivalent resistance resistance between A and B of network shown in figure is
View Solution