Twelve wires, each having resistance r. are joined to form a cube as shown in figure. Find the equivalent resistance between the ends of a face diagonal such as a and c.
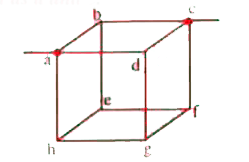
Suppose a potential difference V is applied between the points a and c so that a current i enters at a and the same current leaves at c.
The current distribution is shown in figure
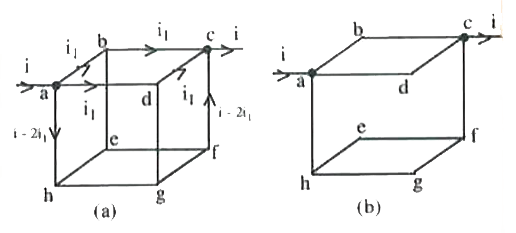
By symmetry, the paths ad and ab are equivalent and hence will carry the same current i1. The path ah will carry the remaining current i−2i1 (using Kirchoff.s junction law).
Similarly at junction c, currents coming from dc and bc will be i1 each and from fc will be i−2i1.
Kirchoff.s junction law at b and d shows that currents through be and dg will be zero and hence may be igonored for further analysis. Omitting these two wires, the circuit is redrawn in figure.
The wire hef and joined in parallel and have equivalent resistance
(2r)(2r)(2r)+(2r)=r
between h and f. This is joined in series with ah and fc giving equivalent resistance
r+r+r=3r
This 3r is joined in parallel with adc (2r) and abc (2r) between a and c.
The equivalent reistance R between a and c is, therefore, given by
1R=13r+12r+12r
∴ Equivalent resistance, R=34r.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE - IA
2 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL -II PRACTICE SHEET (ADVANCED) (Linked Comprehension Type Questions))
9 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - PROBLEMS (LEVEL-II)
27 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - AAKASH SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - PRACTICE EXERCISEX
42 Videos
Similar Questions
Twelve wire, each having resistance r, are joined to form a cube as shown in figure.Find the equivalent resistance between the end of a face diagonal such as aandc.

View SolutionTwelve wire, each having resistance r, are joined to form a cube as shown in figure.Find the equivalent resistance between the end of a face diagonal such as aandc.

View Solution
Knowledge Check
Four identical resistances each having value R are arranged as shown in Figure. Find the equivalent resistance between A and B.
 ARB2RC3RD4R
ARB2RC3RD4R
Twelve wire, each having equal resistance r, are joined to form a cube as shown in figure.Find the equivalent resistance between the diagonally opposite points a and f.

View SolutionTwelve wire, each having equal resistance r, are joined to form a cube as shown in figure.Find the equivalent resistance between the diagonally opposite points a and f.

View SolutionTwelve capacitors, each having capacitors, C, are joined to from a cube as shown. Find the equivalent capacitance between the ends of
(a) Digitonal i.e., between A and B.
(b) Face diagonal i.e., between A and C.
(c) side of cube i.e., between A and D.

View Solution
Twelve indentical resistance each of resistance R are joined to form a cube as shown in figure. Find resistance of the combination across AB.
View Solution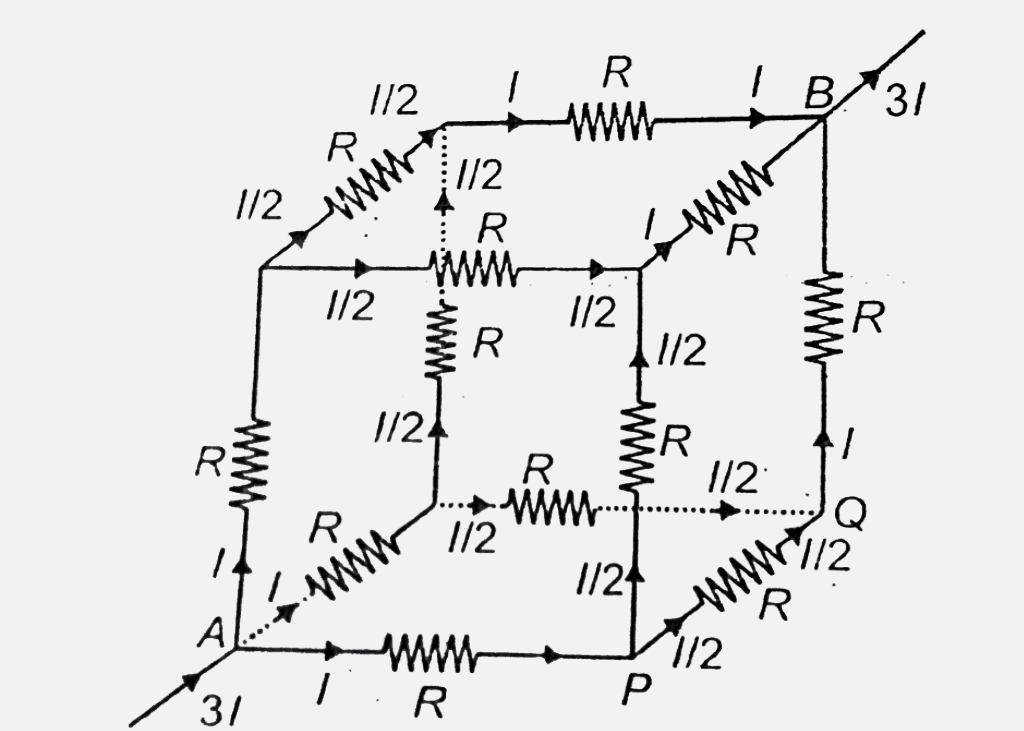
Tweve identical resistance each of resistance R are joined to form a cube as shown in figure.
Find resistance of the combination across AB
View SolutionFour identical resistances each having value R are arranged as shown in Figure. Find the equivalent resistance between A and B.

View SolutionEach resistance of the circuit shown in figure is r. The equivalent resistance between A and B is
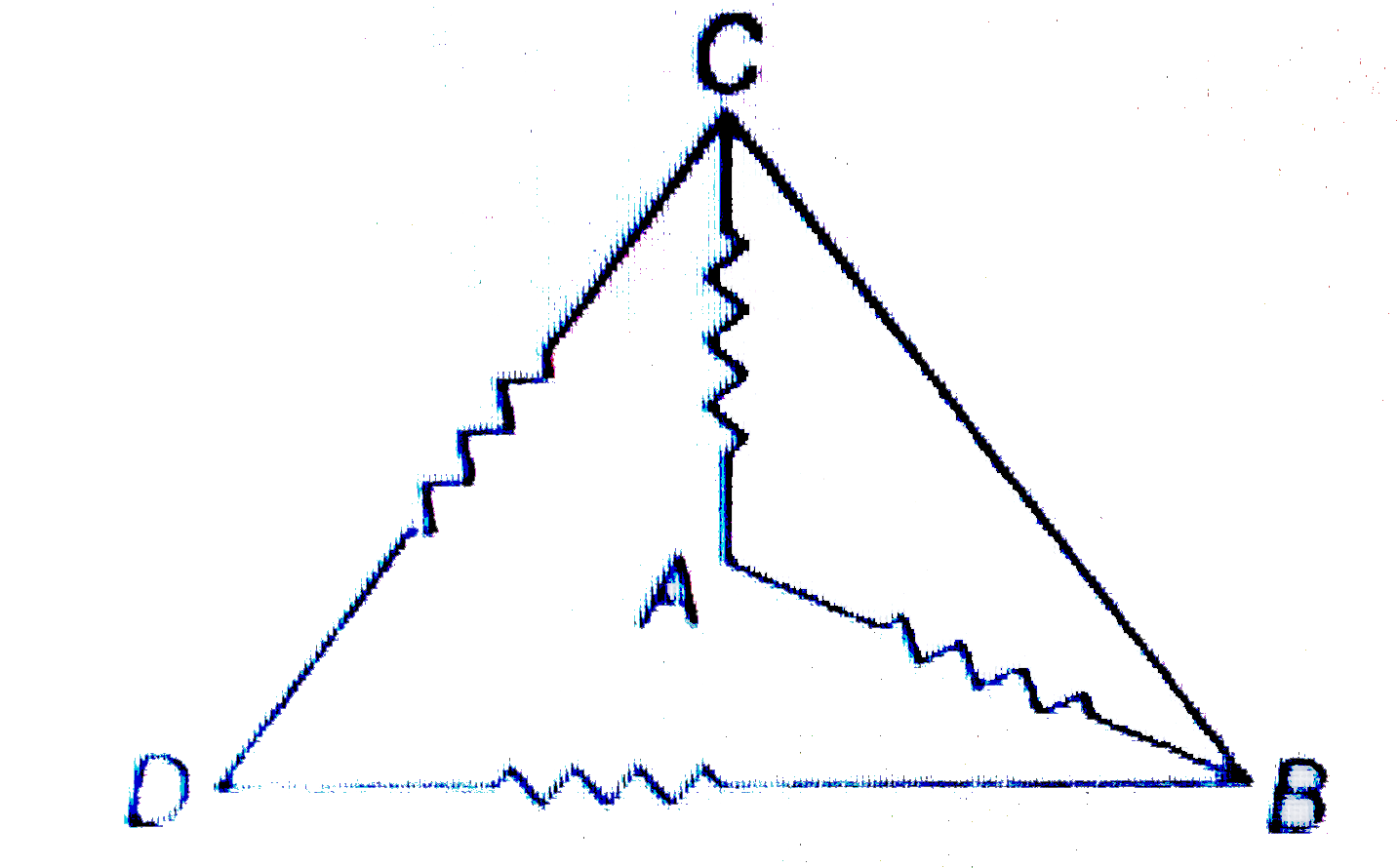
View Solution
