Two absolute scales A and B have triple points of water defined to be 200A and 350B. What is the relation between TA and TB?
To find the relationship between the temperatures on scales A and B, we can use the information given about the triple points of water on these scales.
1. Understand the Triple Point of Water:
The triple point of water is a specific temperature and pressure at which water can coexist in all three phases: solid, liquid, and gas. For the Kelvin scale, this is defined as 273.16 K.
2. Set Up the Relationship:
We know the triple points for scales A and B:
- Triple point of water on scale A: TA=200A
- Triple point of water on scale B: TB=350B
3. Use the Triple Point Relation:
The relationship between the temperatures on different scales can be expressed as:
TKTA=TKTB
where TK is the temperature in Kelvin (273.16 K).
4. Substituting the Values:
Substitute the values of the triple points into the equation:
273.16200=273.16350
5. Cross-Multiply:
Since TK appears on both sides, we can simplify:
273.16⋅350=273.16⋅200
This simplifies to:
350⋅TA=200⋅TB
6. Rearranging the Equation:
Rearranging gives:
TA=200350TB
7. Simplifying the Fraction:
Simplifying 200350 gives:
TA=47TB
Final Result:
The relationship between the temperatures on scales A and B is:
TA=47TB
The triple point of water is a specific temperature and pressure at which water can coexist in all three phases: solid, liquid, and gas. For the Kelvin scale, this is defined as 273.16 K.
We know the triple points for scales A and B:
- Triple point of water on scale A: TA=200A
- Triple point of water on scale B: TB=350B
The relationship between the temperatures on different scales can be expressed as:
TKTA=TKTB
where TK is the temperature in Kelvin (273.16 K).
Substitute the values of the triple points into the equation:
273.16200=273.16350
Since TK appears on both sides, we can simplify:
273.16⋅350=273.16⋅200
This simplifies to:
350⋅TA=200⋅TB
Rearranging gives:
TA=200350TB
Simplifying 200350 gives:
TA=47TB
The relationship between the temperatures on scales A and B is:
TA=47TB
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBOOK - NCERT ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - EXERCISE
22 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - NCERT ENGLISHCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EXERCISE
33 Videos
- THERMODYNAMICSBOOK - NCERT ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - EXERCISE
10 Videos
Similar Questions
Knowledge Check
The graph between two temperature scales A and B is shown in Fig. Between upper fixed point and lower fixed point there are 150 equal divisions on scales A and 100 on scale B. The relation between the temperature in two scales is given by_
_S01_001_Q01.png) ATA−180100=TB150BTA−30150=TB100CTB−180150=TA100DTB−40100=TA180
ATA−180100=TB150BTA−30150=TB100CTB−180150=TA100DTB−40100=TA180
On the absolute scale triple point of water is one fixed temperature, what is the other?
View SolutionTwo bodies A and B having same angular momentum and IA>IB, then the relation between (K.E.)Aand(K.E.)B will be :
View SolutionThe basic difference between B and T-cells is
View SolutionIn the given figure what is the equivalent resistance between two points A and B?
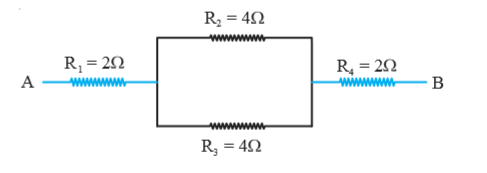
View SolutionTwo samples of DNA, A and B have melting points 340K and 350 K respectively. This is because
View SolutionWhat is the functional difference between B cells and T cells.
View SolutionThe graph between two temperature scales A and B is shown in Fig. Between upper fixed point and lower fixed point there are 150 equal divisions on scales A and 100 on scale B. The relation between the temperature in two scales is given by_
_S01_001_Q01.png)
View Solution