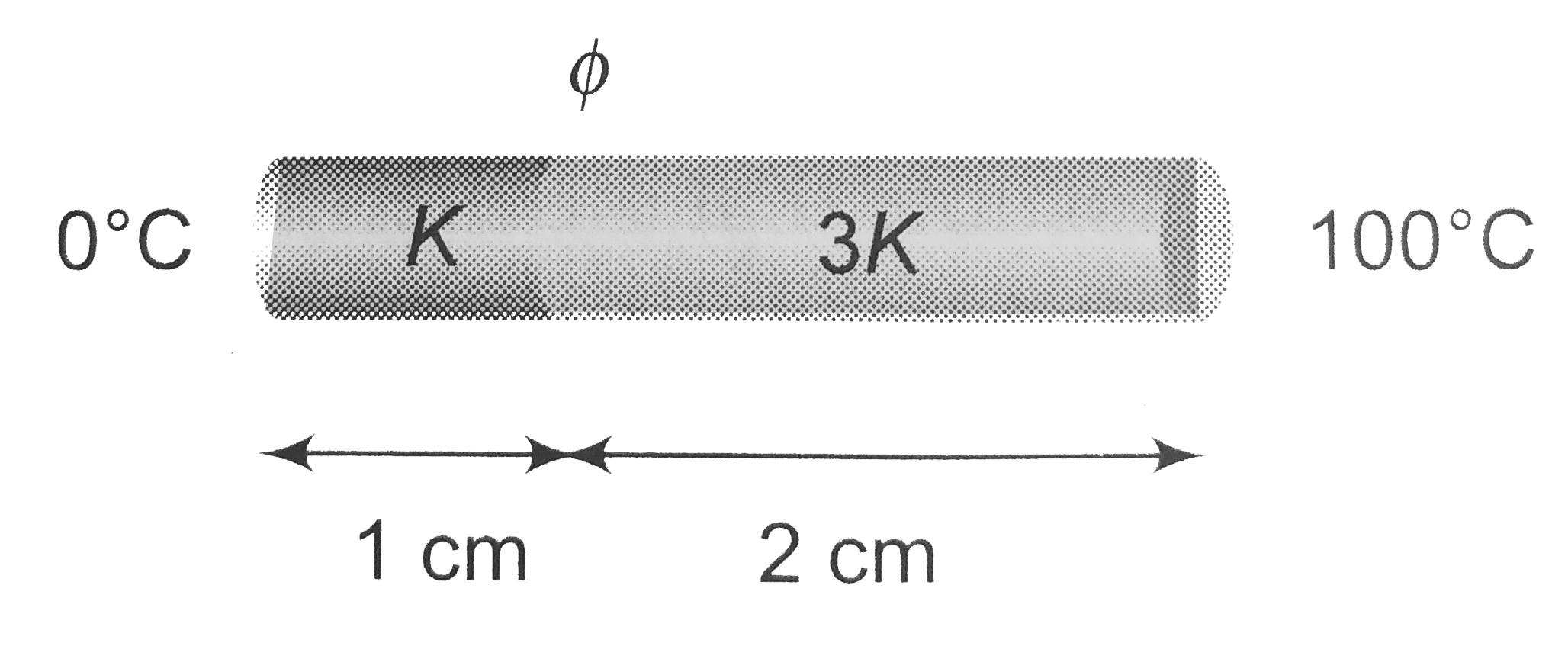
Two bars of thermal conductivities K and 3K and lengths 1cm and 2cm respectively have equal cross-sectional area, they are joined lengths wise as shown in the figure. If the temperature at the ends of this composite bar is 0∘C and K2/l respectively (see figure), then the temperature ϕ of the interface is
50∘C
1003.∘C
60∘C
2003.∘C
The correct Answer is:C
Temperature of interface
θ=K1θ1l2+K2θ2l1K1l2+K2l1=K×0×2+3K×100×1K×2+3K×1
=300K5K=60∘C.
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBOOK - A2ZCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Transmission Of Heat : Radiation
28 Videos
- THERMAL PROPERTIES OF MATTERBOOK - A2ZCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Problems Baesd On Mixed Concepts
18 Videos
- THERMAL PROPERTIES OF MATTERBOOK - A2ZCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Calorimetry
41 Videos
- ROTATIONAL DYNAMICSBOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Chapter Test
29 Videos
- UNIT, DIMENSION AND ERROR ANALYSISBOOK - A2ZCHAPTER - UNIT, DIMENSION AND ERROR ANALYSISEXERCISE - Chapter Test
28 Videos
Similar Questions
Two materials having coefficients of thermal conductivity ‘3 K’ and ‘K’ and thickness ‘d’ and ‘3 d’, respectively, are joined to form a slab as shown in the figure. The temperatures of the outer surfaces are θ2 and θ1 respectively, (θ2>θ1) The temperature at the interface is:
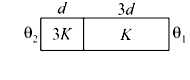
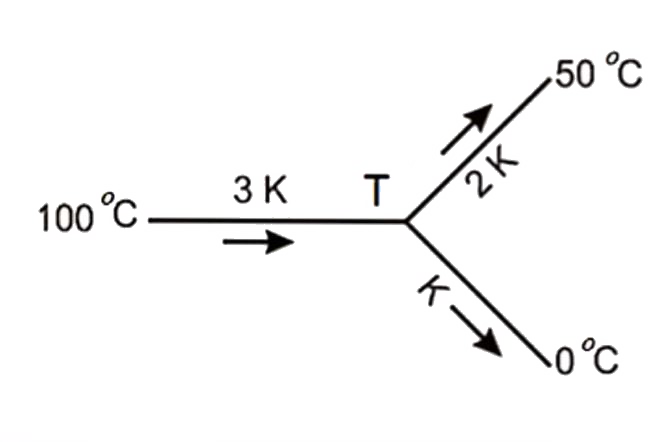
View SolutionThree rods of the same dimension have thermal conductivity 3K, 2K and K as shown in the figure. The temperature of the junction in steady-state is
View Solution
Knowledge Check
Two rods having thermal conductivity in the ratio of 5 : 3 having equal lengths and equal cross-sectional area are joined by face to face. If the temperature of the free end of the first rod is 100∘C and free end of the second rod is 20∘C . Then temperature of the junction is
A70∘CB50∘CC50∘CD90∘CThree rods A, B and C of the same length and same cross-sectional area are joined as shown. Their thermal conductivities are in the ratio 1:2:3/2. If the open ends of A and C are at 200∘C and 18∘C, respectively, then the temperature at the junction of A at steady state is
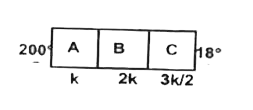A156∘CB148∘CC116∘CD74∘CTwo rods of similar area of cross section and length are joined as shown in the figure. The ratio of their thermal conductivity is 2:3. The free ends are maintained at 100∘C and 0∘C respectivley. THE temperature at junction in steady state is
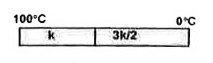A50∘CB40∘CC60∘D80∘C
Three bars of equal lengths and equal area of cross-section are connected in series fig. their thermal conducitives are in the ratio 2:3:4. If at the steady state the open ends of the first and the last bars are at temperature 200∘C and 20∘C respectively, find the temperature of both the junctions.
.
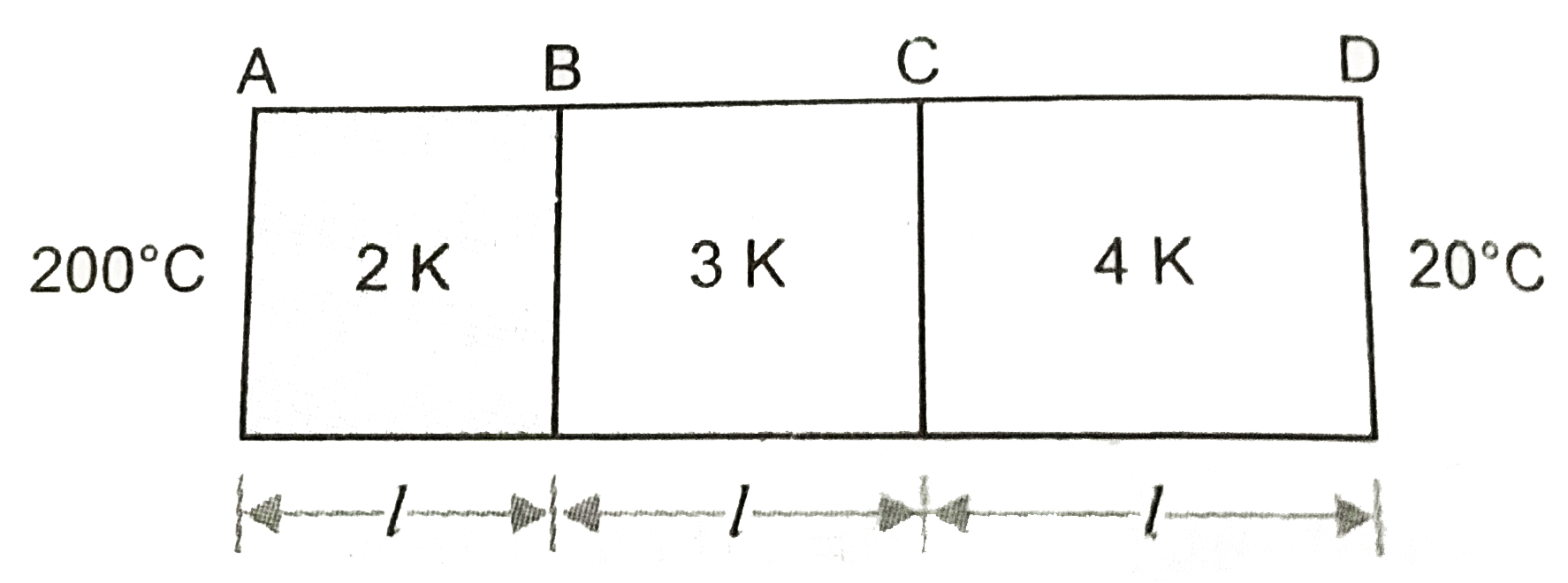View SolutionThree rods of the same dimension have thermal conductivity 3K , 2K and K. They are arranged as shown in the figure below
Then , the temperature of the junction in steady - state is
View SolutionTwo rods of length l and 2l thermal conductivities 2K and K are connected end to end. If cross sectional areas of two rods are eual, then equivalent thermal conductivity of the system is .
View SolutionThree rods of the same dimension have thermal conductivity 3K, 2K and K as shown in the figure. The temperature of the junction in steady-state is
View Solution_2019_CBT4_E01_064_Q01.png)
Two conductors of same cross-section and conductivities K, 3K and length 3 d and d respectively are connected end to end as shown in figure. Temperature of end of first conductor is θ1 and that of second conductor is θ2 .the temperature of junction is steady state is (θ2>θ1)
View Solution