Two materials having coefficients of thermal conductivity ‘3 K’ and ‘K’ and thickness ‘d’ and ‘3 d’, respectively, are joined to form a slab as shown in the figure. The temperatures of the outer surfaces are θ2 and θ1 respectively, (θ2>θ1) The temperature at the interface is:
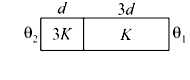
θ16+5θ26
θ110+9θ210
θ2+θ12
θ13+2θ23
The correct Answer is:B
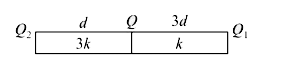
ddQdt=3KA(θ2−θ)d=KA(θ−θ1)3d
θ=θ110+9θ210
Similar Questions
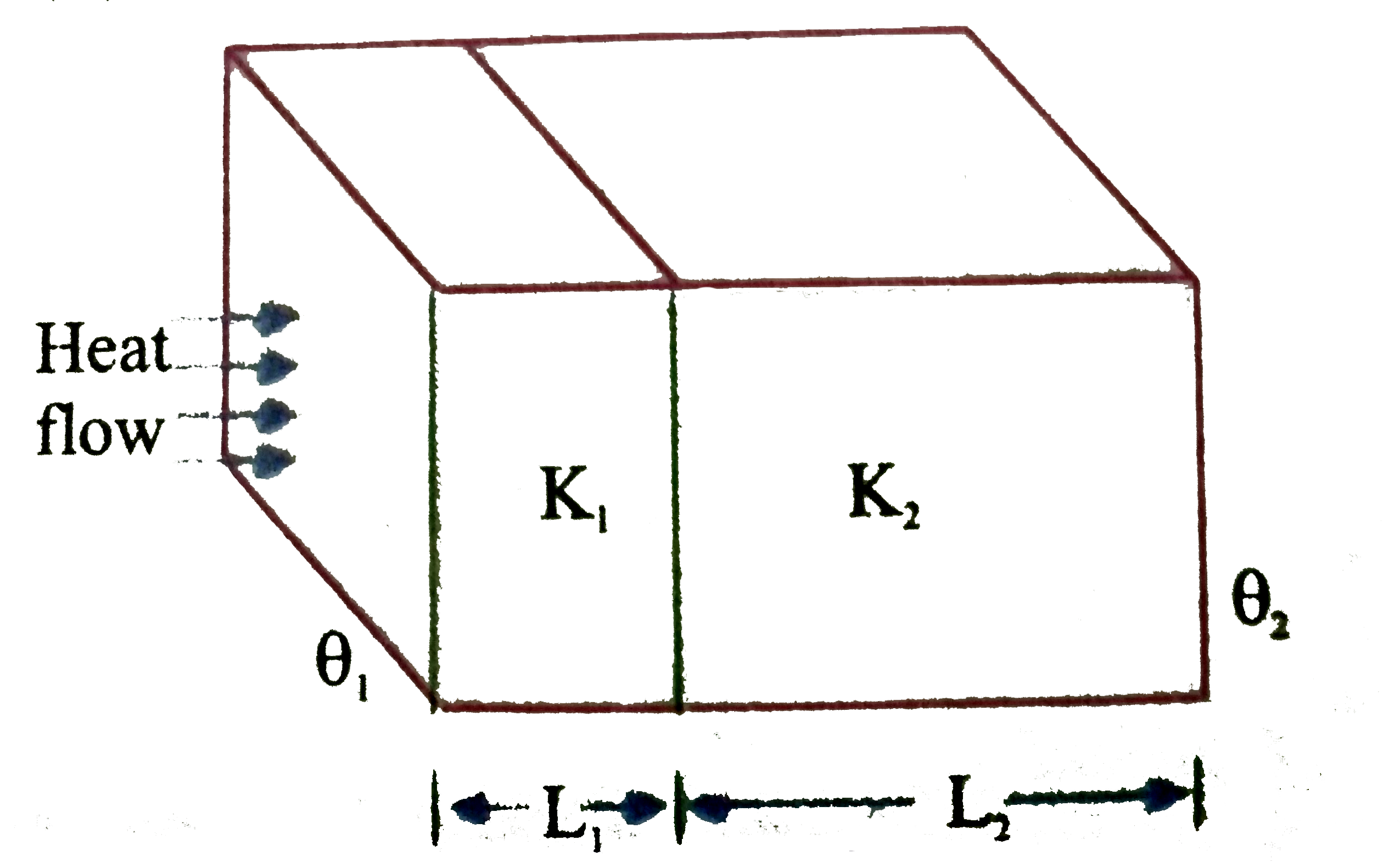
Two plates each of area A thickness L1 and L2 thermal conductivities K1 and K2 respectively are joined to from a single plate of thickness (L1+L2) If the temperatures of the free surfaces are θ1 and θ2 Calculate
(a) Rate of flow of heat
(b) Temperature of interface
 .View Solution
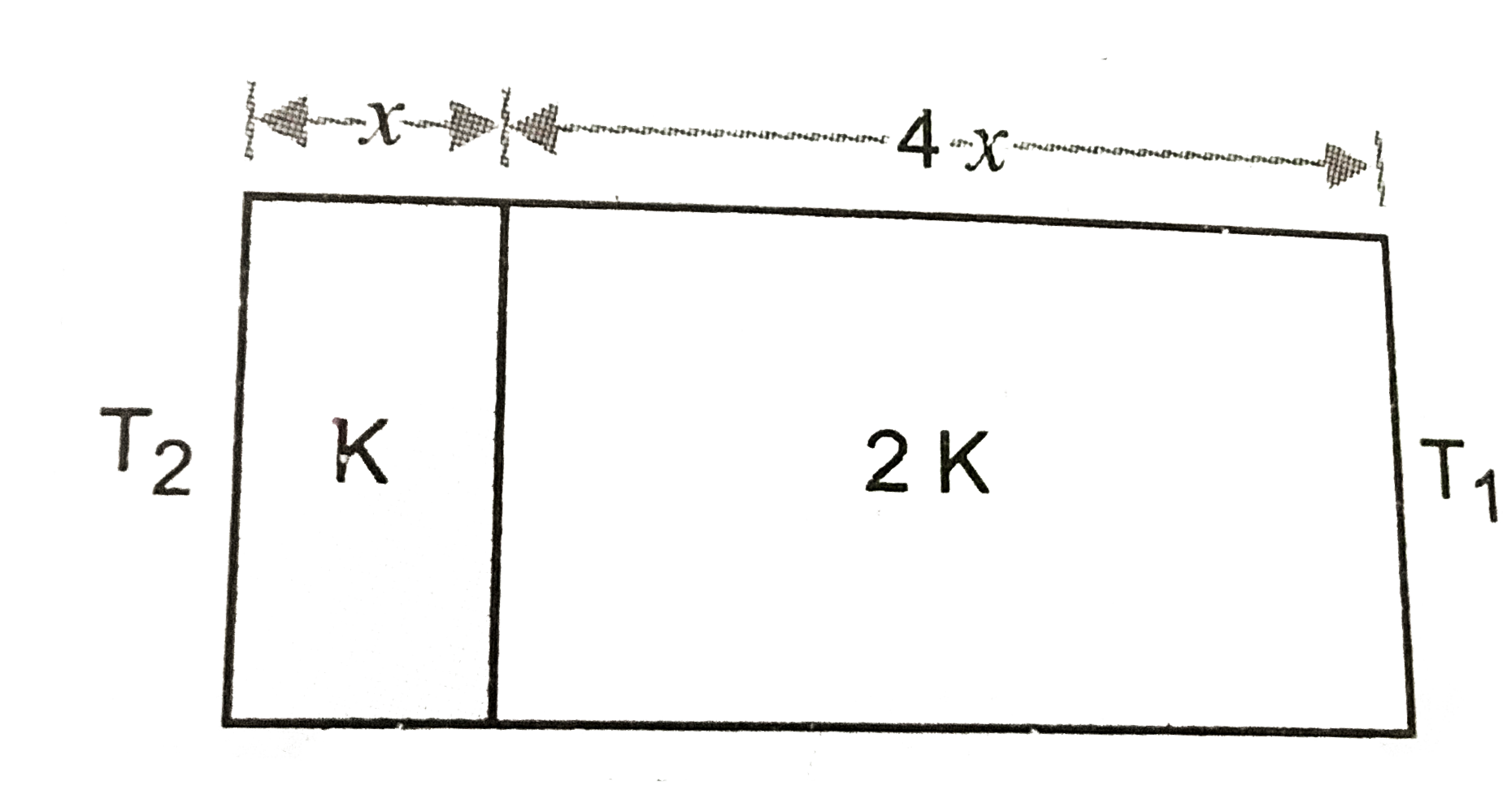
.View SolutionThe temperature of the two outer surfaces of a composite slab, consisting of two materials having coefficients of thermal conductivity K and 2K and thickness x and 4x respectively. Temperatures on the opposite faces of composite slab are T1andT2 where T2>T1, as shown in fig. what is the rate of flow of heat through the slab in a steady state?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two bars of thermal conductivities K and 3K and lengths 1cm and 2cm respectively have equal cross-sectional area, they are joined lengths wise as shown in the figure. If the temperature at the ends of this composite bar is 0∘C and K2/l respectively (see figure), then the temperature ϕ of the interface is
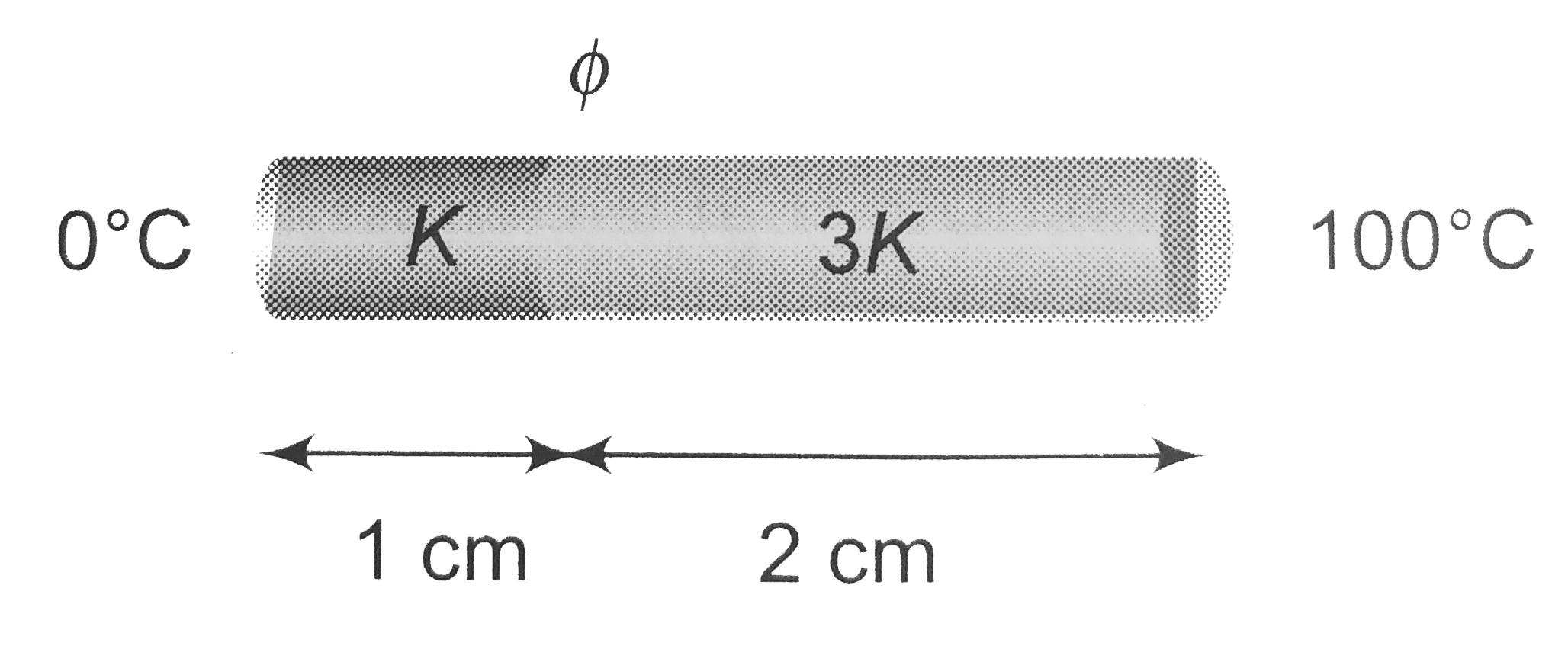 A50∘CB1003.∘CC60∘CD2003.∘C
A50∘CB1003.∘CC60∘CD2003.∘C - Question 2 - Select One
If two conducting slabs of thickness d1 and d2, and thermal conductivity K1 and K2 are placed together face to face as shown in figure in the steady state temperature of outer surfaces are θ1 and θ2. The temperature of common surface is-
 AK1θ1d1+K2θ2d2K1d1+K2d2BK1θ1+K2θ2K1+K2CK1θ1+K2θ2θ1+θ2DK1θ1d2+K2θ2d1K1d2+K2d1
AK1θ1d1+K2θ2d2K1d1+K2d2BK1θ1+K2θ2K1+K2CK1θ1+K2θ2θ1+θ2DK1θ1d2+K2θ2d1K1d2+K2d1 - Question 3 - Select One
_2019_CBT4_E01_064_Q01.png)
Two conductors of same cross-section and conductivities K, 3K and length 3 d and d respectively are connected end to end as shown in figure. Temperature of end of first conductor is θ1 and that of second conductor is θ2 .the temperature of junction is steady state is (θ2>θ1)A10θ2+9θ119Bθ2+9θ10C9θ2+θ110D9θ2+10θ119
Two plates eachb of area A, thickness L1andL2 thermal conductivities K1andK2 respectively are joined to form a single plate of thickness (L1+L2). If the temperatures of the free surfaces are T1andT2. Calculate.

(a) rate of flow of heat
(b) temperature of interface and
(c) equivalent thermal conductivity.View SolutionIf two conducting slabs of thickness d1 and d2, and thermal conductivity K1 and K2 are placed together face to face as shown in figure in the steady state temperature of outer surfaces are θ1 and θ2. The temperature of common surface is-
 View Solution
View SolutionIn the following figure, two insulating sheets with thermal resistances R and 3 R as shown in figure. The temperature θ is
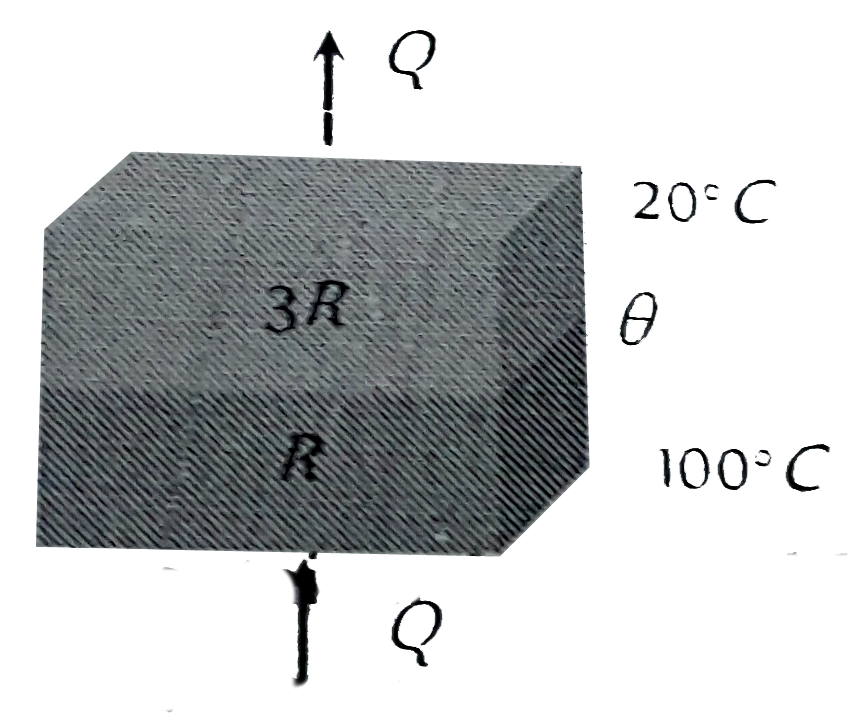 View Solution
View SolutionConsider the two insulating sheets with thermal resistance R1 and R2 as shown in figure. The temperature θ is
 View Solution
View SolutionThree identical solid spheres (1, 2 and 3) are allowed to roll down from three inclined plane of angles θ1,θ2andθ3 respectively starting at time t = 0, where θ1>θ2>θ3, then
View Solution

