Two batteries each of emf E and internal resistance r are connected in series and in parallel, and are used to find current in an external resistance R. If the current in series is equal to that in parallel, the internal resistance of each battery is
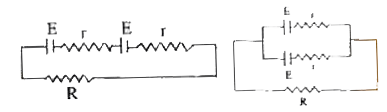
Is=2E2r+RandIP=Er2+R=2Er+2R
If IS+IP, (2E)/(2R+R)=(2E)/(r+2R), 2r+R=r+2R rArr r=R
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE - IA
2 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL -II PRACTICE SHEET (ADVANCED) (Linked Comprehension Type Questions))
9 Videos
- CURRENT ELECTRICITYBOOK - AAKASH SERIESCHAPTER - CURRENT ELECTRICITYEXERCISE - PROBLEMS (LEVEL-II)
27 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - AAKASH SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - PRACTICE EXERCISEX
42 Videos
Similar Questions
Five identical cells each of internal resistance 1Ω and emf 5V are connected in series and in parallel with an external resistance 'R' . For what value of 'R', current in series and parallel combination will remain the same ?
View SolutionTwo batteries each of emf ε and internal resistance r, are connected in parallel. If we take current from this combination in a external resistance R, then for what value of R maximum power will beobtained? What will be this power?
View Solution
Knowledge Check
Two batteries each of E and internal resistance r are connected turn by turn in series and in parallel, and are used to find current in an external resistance R. If the current in series is equal to that in parallel, the internal resistance of each battery is
ARBR/2CR/3DR/4N batteries each of emf E and internal resistance r are first connected in series and then in parallel to an external resistance R. if current through R is same in both cases then.
AR=r2/NBR−Nr/2CR=NrDR=rTwo batteries of difference emf's and internal resistance are connected in parallel to one another.
AEquivalent emf will be grater than either of the emf'sBEquivalent emf will be smaller than either of the emfCEquivalent internal resistance will be grater than either of the two internal resistancesDEquivalent internal resistance will be smaller than either of the two internal resistances.
Two batteries each of emf ε and internal resistance r, are connected in parallel. If we take current from this combination in a external resistance R, then for what value of R maximum power will beobtained? What will be this power?
View SolutionFour cells, each of emf E and internal resistance r, are connected in series across an external resistance reverse. Then, the current in the external circuit is
View SolutionFour cell each of emf 2 V and internal resistance 1 ohm are connected n parallel with an external resistance of 6 ohm. The current in the external resistance is
View Solutionn identical cells, each of emf e volt and internal resistance rΩ are connected in a row m. Such rows are connected in parallel. This battery sends current through an external resistance R. The current will be maximum if
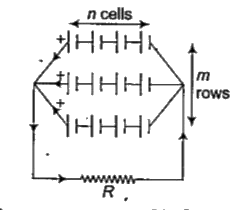
View Solutionn identical cells, each of emf e volt and internal resistance rΩ are connected in a row m. Such rows are connected in parallel. This battery sends current through an external resistance R. The current will be maximum if
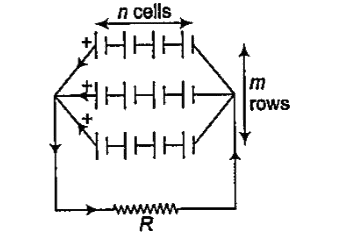
View Solution
